Коткин Г. Всплывающий воздушный пузырек и закон Архимеда// Квант
Коткин Г. Всплывающий воздушный пузырек и закон Архимеда // Квант. – 1976. – № 1. – С. 19-23. (1996. – № 3. – С. 50-51.)
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Представьте себе, что вы готовитесь к экзамену по физике, расположившись на лесной опушке на берегу озера. Повторяя второй закон Ньютона, бы хотите применить этот закон к движению всплывающих со дна пузырьков газа. И тут начинается что-то странное...
Сила тяжести, действующая на пузырек, раз в тысячу меньше веса вытесняемой им воды (плотности воздуха и воды отличаются примерно в тысячу раз). Сила сопротивления при жидком трении, пропорциональная скорости пузырька, поначалу мала, поэтому ее учитывать не стоит (О роли силы сопротивления будет сказано дальше.). Таким образом, ускорение определяется, в основном, архимедовой выталкивающей силой:
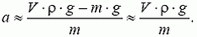 (1)
(1)
Здесь m – масса, а – ускорение пузырька, V – его объем, ρ – плотность воды. Пусть плотность газа ρ0. Тогда
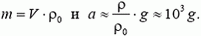
Итак, ускорение пузырька порядка тысячи g. Это очень большая величина. Вспомним, что ускорение, которое приходится переносить космонавтам к летчикам, достигает нескольких g (скажем, до 10g). Если снаряд будет двигаться в стволе длиной 1 м с таким ускорением, то он сможет взлететь на высоту h = 1 км (проверьте это самостоятельно); если внутрь нашего всплывающего пузырька попадет букашка, она будет раздавлена в таком «лифте»; и т.д. и т.п. Поистине богатые возможности для изобретателей.
Впрочем, сидя на берегу озера, можно увидеть собственными глазами, что на самом деле ускорение пузырька вовсе не так велико.
Вместо того чтобы сразу дать ответ на возникшую загадку, зададим еще одну.
Пусть вы без труда можете поднять пудовую гирю (m = 16 кг) на высоту 1 м. А что если приложить силу, равную весу этой гири, к камешку массы 1 г (или к копеечной монете) на пути тоже в 1 м? Нетрудно сообразить, что камешек после этого взлетит на высоту 16 км. (Сопротивление воздуха не учитываем. Ясно, что дело не в нем.) Что это – еще один фантастический проект? Нет, на этот раз разоблачить автора проекта совсем легко: поднимать придется не только камешек, но и собственную руку! К каждому ее грамму нужно приложить силу порядка 160 Н. Вся рука будет весить несколько тонн, и поднять ее не хватит сил.
Таким образом, неподвижная или движущаяся с небольшим ускорением рука может приложить к грузу силу гораздо большую, чем рука, которая движется с большим ускорением.
Но ведь при движении воздушного пузырька в воде возникает аналогичная картина. Когда пузырек поднимается, некоторая масса воды устремляется вниз, заполняя освобожденное место. Пузырек взаимодействует с движущейся, а не с неподвижной водой. По-видимому, и сила, действующая со стороны воды на пузырек, зависит от ускорения самой воды. Закон Архимеда, записанный в обычном виде 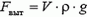 , неприменим к пузырьку, движущемуся ускоренно!
, неприменим к пузырьку, движущемуся ускоренно!
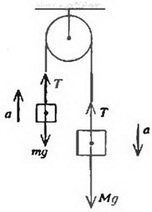
Рис. 1.
Оказывается, задача о пузырьке очень близка к задаче о движении грузиков, связанных переброшенной через неподвижный блок нитью (рис. 1). Нетрудно увидеть аналогию между ними. Действительно, один из грузиков (с массой m) как бы играет роль пузырька, другой (с массой М) – роль воды, а натяжение нити Т – роль выталкивающей силы.
Второй закон Ньютона в применении к грузику массы m можно записать так:
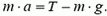 (2)
(2)
Если грузик массы m удерживать, то натяжение нити Т окажется численно равным весу грузина Mg (весу «вытесненной» воды). Подставив 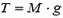 в уравнение (2), получаем:
в уравнение (2), получаем:
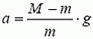 (неверно!). (3)
(неверно!). (3)
При 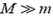 оказывается
оказывается 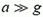 . Этот вывод своей нелепостью похож на вывод об огромном ускорении пузырька (см. (1)). Причина обеих ошибок одна и та же: необходимо учитывать движение грузика массы М и движение «вытесненной» воды. Напомним, что для правильного решения задачи о грузиках нужно записать еще уравнение второго закона Ньютона для грузика массы М
. Этот вывод своей нелепостью похож на вывод об огромном ускорении пузырька (см. (1)). Причина обеих ошибок одна и та же: необходимо учитывать движение грузика массы М и движение «вытесненной» воды. Напомним, что для правильного решения задачи о грузиках нужно записать еще уравнение второго закона Ньютона для грузика массы М
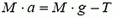 (4)
(4)
и решить систему уравнений (2) и (4). Отсюда
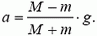 (5)
(5)
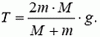
При 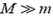 оказывается
оказывается 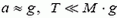 , что вполне соответствует действительности.
, что вполне соответствует действительности.
Можно решить эту задачу и другим способом – воспользоваться законом сохранения энергии. При смещении грузика массы m вверх (и соответственно, грузика массы М вниз) на расстояние h потенциальная энергия системы уменьшится на величину 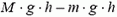 . Кинетическая энергия станет равной
. Кинетическая энергия станет равной 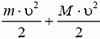 , где υ – скорость грузиков (начальную скорость считаем равной нулю). Приравняв величины
, где υ – скорость грузиков (начальную скорость считаем равной нулю). Приравняв величины
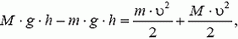
находим
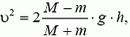
или (см. (5))
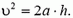 (6)
(6)
Такая связь скорости и перемещения характерна для движения с постоянным ускорением а. (В данном случае 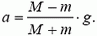 )
)
Воспользуемся этим для решения задачи о движении тела в жидкости. Правда, привести полное решение задачи о воздушном пузырьке мы не сможем. Дело в том, что распределение скоростей жидкости вокруг пузырька слишком сложно (рис. 2).
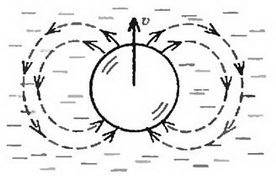
Рис. 2.
Однако мы решим похожую задачу. Рассмотрим движение длинного стержня радиуса r, длины l и массы m вдоль оси заполненной жидкостью плотности с трубки радиуса 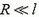 (рис. 3).
(рис. 3).
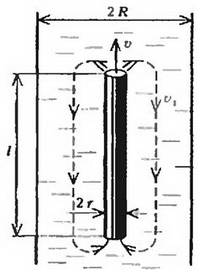
Рис 3.
В этом случае движение жидкости легко рассчитать. Вытесняемая верхней частью стержня жидкость смещается вниз и заполняет место, освобождаемое нижней частью стержня. Если исключить небольшие участки вблизи торцов стержняt то скорость жидкости всюду между стержнем и стенками трубки оказывается одной и той же. Обозначим через υ скорость стержня, а через υ1 —скорость воды, движущейся между стержнем и стенками трубки, в тот момент, когда стержень поднялся на высоту h от того уровня, на котором его скорость была равна нулю. Приравняв объем 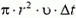 жидкости, вытесненной стержнем за малый промежуток времени Δt, объему
жидкости, вытесненной стержнем за малый промежуток времени Δt, объему 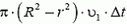 жидкости, прошедшей за это же время между стержнем и трубкой, находим
жидкости, прошедшей за это же время между стержнем и трубкой, находим
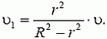
За то время, пока стержень поднимался на высоту h, масса жидкости, равная 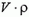 (
(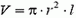 – объем стержня), опустится тоже на h, тогда уменьшение потенциальной энергии стержня и жидкости равно
– объем стержня), опустится тоже на h, тогда уменьшение потенциальной энергии стержня и жидкости равно 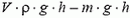 . Кинетическая энергия системы равна
. Кинетическая энергия системы равна 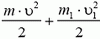 , где m1 – масса движущейся жидкости. Кинетическую энергию жидкости удобно записать в таком виде:
, где m1 – масса движущейся жидкости. Кинетическую энергию жидкости удобно записать в таком виде:
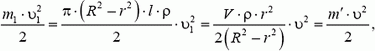
где 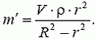
Воспользовавшись законом сохранения энергии, получим
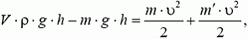
откуда
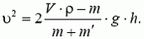
Такой зависимости скорости υ от перемещения h отвечает движение с ускорением (см. (6))
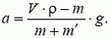 (7)
(7)
Таким образом, стержень движется так, будто бы его масса увеличилась на величину m', а выталкивающая сила осталась равной гидростатической архимедовой силе 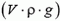 . Величину m' называют присоединенной массой. Это чисто формальное, но удобное толкование равенства (7). Формула (7) получается из неправильной формулы (1) добавлением в знаменателе слагаемого m'. Отметим, что подобным же образом формула (5) получается из (3) добавлением в знаменателе слагаемого М.
. Величину m' называют присоединенной массой. Это чисто формальное, но удобное толкование равенства (7). Формула (7) получается из неправильной формулы (1) добавлением в знаменателе слагаемого m'. Отметим, что подобным же образом формула (5) получается из (3) добавлением в знаменателе слагаемого М.
Силу Fвыт, с которой движущаяся жидкость действует на стержень, теперь легко получить из второго закона Ньютона
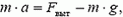
откуда
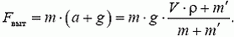 (8)
(8)
В частности, если 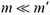 , то
, то 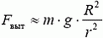 ; при
; при  выталкивающая сила оказывается порядка веса стержня (и не имеет отношения к весу вытесненной воды). Если же
выталкивающая сила оказывается порядка веса стержня (и не имеет отношения к весу вытесненной воды). Если же 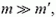 то
то 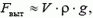 то есть мы возвращаемся к закону Архимеда в обычном виде.
то есть мы возвращаемся к закону Архимеда в обычном виде.
< style="text-transform: uppercase">Для шарика (в частности, для пузырька) расчет дает такой результат: кинетическая энергия жидкости равна 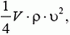 где V – объем шарика, υ – его скорость. Тогда присоединенная масса для пузырька
где V – объем шарика, υ – его скорость. Тогда присоединенная масса для пузырька 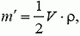 т.е. она равна половине массы вытесненной воды. Пузырек всплывает с ускорением
т.е. она равна половине массы вытесненной воды. Пузырек всплывает с ускорением
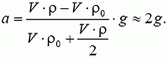
Выталкивающая сила определяется из уравнения (8), она приблизительно равна 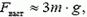 т.е. тройному весу неподвижного пузырька (и во много раз меньше веса вытесненной воды).
т.е. тройному весу неподвижного пузырька (и во много раз меньше веса вытесненной воды).
Теперь вспомним о силе сопротивления, Для пузырька газа в жидкости она определяется формулой 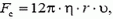 где r – радиус пузырька, υ – его скорость, η – так называемый коэффициент вязкости среды (Приведенная формула справедлива при
где r – радиус пузырька, υ – его скорость, η – так называемый коэффициент вязкости среды (Приведенная формула справедлива при 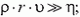 если
если 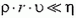 , коэффициент 12πследует заменить на 4π. Дли твердого шарика при
, коэффициент 12πследует заменить на 4π. Дли твердого шарика при 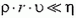 коэффициент равен 6π (формула Стокса).). С учетом силы сопротивления уравнение движения пузырька запишется так (см. (7)):
коэффициент равен 6π (формула Стокса).). С учетом силы сопротивления уравнение движения пузырька запишется так (см. (7)):
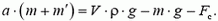 (9)
(9)
Очевидно, что Fс уменьшает ускорение (а значит, и скорость) пузырька по сравнению с тем случаем, когда мы не учитываем сопротивление жидкости. Однако, если 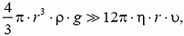 т.е. при
т.е. при 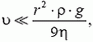 силой сопротивления можно пренебречь. Например, если речь идет о пузырьке радиуса r = 3 мм (Пузырек большего радиуса не может сохранить шарообразную форму (подобно падающей дождевой капле, деформируемой силой давления воздуха; см., например, статью И.Ш. Слободецкого «О форме дождевой капли», «Квант», 1970, № 8).), движущемся в воде (ρ = 1 г/см3, η = 1,0•10–2 г/(см•с), то его скорость должна быть много меньше величины
силой сопротивления можно пренебречь. Например, если речь идет о пузырьке радиуса r = 3 мм (Пузырек большего радиуса не может сохранить шарообразную форму (подобно падающей дождевой капле, деформируемой силой давления воздуха; см., например, статью И.Ш. Слободецкого «О форме дождевой капли», «Квант», 1970, № 8).), движущемся в воде (ρ = 1 г/см3, η = 1,0•10–2 г/(см•с), то его скорость должна быть много меньше величины 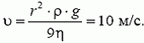 Прикинем, на каком пути h0, пузырек достигнет такой скорости. Для грубой опенки воспользуемся равенством
Прикинем, на каком пути h0, пузырек достигнет такой скорости. Для грубой опенки воспользуемся равенством 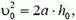 где
где 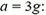
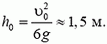
Таким образам, на пути 1,5 м силой сопротивления можно пренебречь. При этом υ0 = 10 м/с – это предельная скорость, которой может достичь всплывающий пузырек газа в воде.
Упражнения
1. Цилиндрическая труба, состоящая из двух частей с радиусами R1 и R2 (рис. 4), соединенных плавным переходом, заполнена водой. Вдоль осп трубы движется длинный стержень радиуса r и плотности ρ0. Скорость стержня а левой части трубы равна υ1. Какой станет его скорость после перехода в правую часть трубы?
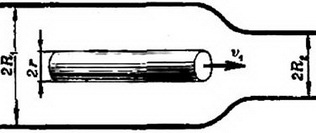
Рис. 4.
2. В жидкости плотности ρ плавает шарик радиуса R с трубкой радиуса 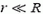 . (рис. 5). Масса шарика с трубкой ранка m. Шарик удален от поверхности жидкости, дна и стенок сосуда на расстояние, много большее его радиуса. Шарик слегка приподняли за трубку и отпустили. Определить период возникших колебаний шарика.
. (рис. 5). Масса шарика с трубкой ранка m. Шарик удален от поверхности жидкости, дна и стенок сосуда на расстояние, много большее его радиуса. Шарик слегка приподняли за трубку и отпустили. Определить период возникших колебаний шарика.

Рис. 5.
3. Вдоль оси трубки с водой всплывает стержень массы m (рис. 6). Определить силу, действующую на дно.
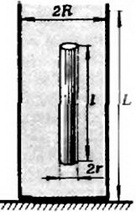
Рис. 6.
Ответы
1. Из закона сохранения энергии 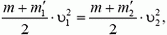 где
где 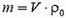 (V – объем стержня),
(V – объем стержня), 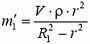 (ρ —плотность поды),
(ρ —плотность поды), 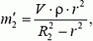 находим
находим 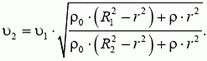
2.  (Решение задачи см., например, в «Кванте», 1974, № 6, с. 36. Только нужно m заменить на
(Решение задачи см., например, в «Кванте», 1974, № 6, с. 36. Только нужно m заменить на 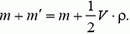
3. Запишем второй закон Ньютона для стержня, для массы 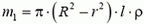 воды, движущейся между стержнем и стенками трубки, и для остальной, неподвижной воды массы
воды, движущейся между стержнем и стенками трубки, и для остальной, неподвижной воды массы 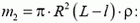
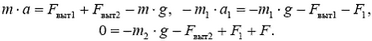
Здесь Fвыт1 (Fвыт2) – сила, с которой движущаяся (неподвижная) вода действует на стержень, F1 – сила взаимодействия < style="text-transform: uppercase">подвижной и неподвижной воды, F – сила, с которой на неподвижную воду действует дно трубки. Сложив все три уравнения, исключаем силы Fвыт1, Fвыт2 и F1. Заметим, что 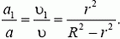 Тогда после несложных преобразовании получаем:
Тогда после несложных преобразовании получаем:
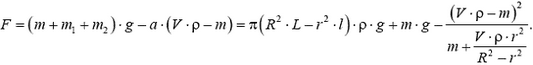
Отсюда видно, что сила давления воды на дно (численно равная силе F) меньше суммарного веса волы и стержня. Причем это справедливо и когда стержень всплывает 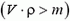 , и когда он тонет
, и когда он тонет 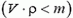 .
.
| Выложил | alsak |
| Опубликовано | 22.07.09 |
| Просмотров | 28290 |
| Рубрика | Решение задач |
| Тема | Гидростатика |