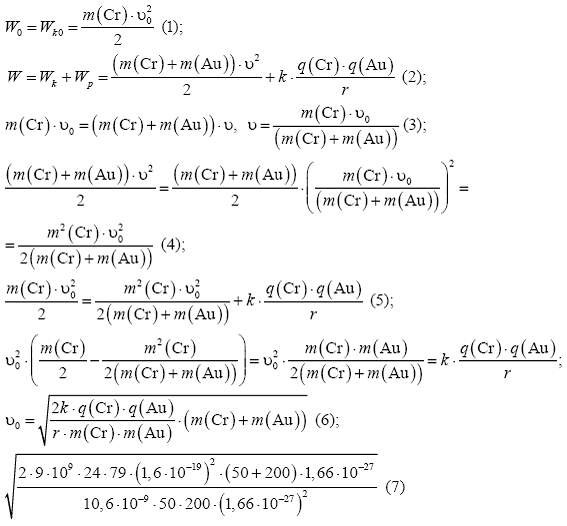репетиционное тестирование 3 этап 2008/2009

[alsak]

Спасибо всем за решения.
А13 Вариант 5
Конденсатор подключают к источнику постоянного тока, напряжение на клеммах которого U₁ = 50 В. При подключении этого конденсатора к источнику с напряжением U₂ = 100 В, электроемкость конденсатора

1) увеличится в 2 раза; 2) уменьшится в 2 раза; 3) увеличится в 4 раза;
2) уменьшится в 4 раза; 5) останется неизменной.

Решение. Емкость конденсатора не зависит от напряжения и заряда на нем (а от площади пластин, расстояния между ними и диэлектрика). Поэтому куда бы вы конденсатор не подключали, емкость его не изменится.

Ответ: 5) останется неизменным.

[alsak]

В4 Вариант 6.
Свободные ядро изотопа  \[ \left({}_{79}^{200}{\rm Au} \right) \] и ядро изотопа хрома  \[ \left({}_{24}^{50} {\rm Cr} \right) \] находятся на большом расстоянии друг от друга. Ядру хрома сообщили скорость, направленную вдоль прямой, соединяющей его с ядром золота. Если минимальное расстояние, на которое сблизились ядра, r = 10,6 нм, то модуль начальной скорости υ₀ ядра хрома был равен … км/с.

Решение. И в этой задаче составители выходят за программу ЦТ этого года (потенциальная энергия взаимодействия точечных зарядов). В таких случаях вы имеете право написать замечание о не соответствии данного задания «Программе вступительных испытаний … 2008 года».
Решаем задачу через закон сохранения энергии. В начальном состоянии система ядра хрома-золота обладают только кинетической энергией хрома (уравнение (1)), где m(Cr) = 50 а.е.м. (не забудьте сделать перевод к кг) – масса ядра хрома; энергией взаимодействия ядер пренебрегаем, т.к ядра находятся на большом расстоянии друг от друга. В конечном состоянии их энергия находится по формуле (2), где учитываем, что минимальное расстояние будет в случае, когда два ядра будут двигаться с одинаковой скоростью в одном направлении (ОБРАТИТЕ ВНИМАНИЕ, многие делают ошибку, и считают что минимальное расстояние будет в случае, когда скорости ядер будут равны нулю. Это не так, и противоречит закону сохранения импульса). Здесь так же учли потенциальную энергию взаимодействия точечных зарядов, находящихся на расстоянии r. Заряды ядер равны q(Cr) = 24e; q(Au) = 79e, где е – элементарный заряд. Масса ядра m(Au) = 200 а.е.м.
Общую скорость найдем из закона сохранения импульса в проекции на ось, направленную вдоль начальной скорости движения хрома (уравнения 3). С учетом этого кинетическая энергия ядер будет равна (4).
В итоге приравняем энергии и решим уравнение (5) относительно начальной скорости. Получаем конечную формулу (6) и ответ, после подстановки чисел (7): 35232 м/с = 35 км/с.

[SHEPARD]

Извините...а вы не могли бы помочь с решением задач А14 и Б1 из 5-ого варианта пробного Цт???

И ещё...почему в задаче B7 5-ого варианта правильный ответ не не 19??? Я нашёл F2, когда заряды изменили..оно получилось равным 57. В ответ они просят дельта F...значит оно будет 76-57=19 мКл. Где у меня ошибка???

[FabrEgAZ]

alsak писал(а):

m2 = 140 г.

У меня тоже 140!B)

[FabrEgAZ]

Paul писал(а):

меня ещё интересуют задания А16(1) и А13(5)...

В A 16 я условие не могу понять :S

[klukva]

Огромное спасибо)))))))))))

[INK]

Если можно,то напишите решение А15 - 6 вариант

[FabrEgAZ]

5-ый вариант


1 12
2 18
3 3
4 111 :laugh:
5 44
6 500 :laugh:
7 57
8 12
9 101 (думаю, что неправильно)
10 450 :laugh: :laugh:
11 3
12 36

[SoReL]

В задаче В4 из 6-ого варианта у меня получается 35 км/с при той же формуле

[INK]

извините если отвлекаю. Напишите пожалуйста решение 6 вариант -В2 и В9