Давиденко А.А. Дисгармония - проблема - противоречие – задача
Давиденко А.А. Дисгармония - проблема - противоречие – задача // Фiзiка: праблемы выкладання. – 2006. – № 4. – С. 37-40.
Наивысшим уровнем творчества человека является все же не умение решать нестандартные задачи, которые ставятся перед ним в готовом виде, а умение ощущать, видеть, выявлять в окружающем мире дисгармонию, несогласованность в действиях отдельных элементов определенной системы (далее все это будем называть дисгармонией), умение формулировать проблему, умение выявлять противоречия между отдельными элементами системы с последующей постановкой на основе этого задачи и ее решением.
Чтобы понять, почему явление, ежедневно и всеми видимое в продолжении двадцати столетий, не обращало на себя внимание физиков, надобно вспомнить, что немногие одарены способностью удивляться кстати.
Франсуа Араго
Деятельностью, которая способствует развитию творческих способностей учащихся, традиционно считается процесс решения творческих задач [1–3]. Для повышения его эффективности разработаны отдельные приемы. Если иметь в виду творческие задачи, имеющие технические решения (изобретательские, конструкторские и рационализаторские), то к таким приемам можно отнести: измельчение (зубы ковша экскаватора выполнить не в виде сплошной гребенки, а изготовить их отдельными, что даст возможность осуществлять замену отдельного зуба, а не всей гребенки, в которой пришел в негодность лишь один зуб); выполнение наперед (спущенную камеру велосипеда во время спортивных соревнований можно наполнить воздухом, который предварительно нагнетают в баллончик); совмещение функций (засыпанное в кузов автомобиля зерно перемешивается установленными в нем шнеками, чем обеспечивается его сушка уже во время перевозки к месту очистки и хранения) и т.п. Такие приемы действительно ускоряют поиски решений творческих задач [4; 5, с. 114–129]. Давно известны методы, которое активизируют поиски решений творческих задач: метод фокальных объектов, морфологический анализ, мозговой штурм, синектика, метод контрольных вопросов и др. [6, с. 41 – 57].
Имели место попытки алгоритмизации процесса творчества. Г.С.Альтшуллером (литературный псевдоним – Г. Альтов), например, была разработана «теория решения изобретательских задач» (ТРИЗ), все последующие этапы развития которой сопровождались усовершенствованием предписаний действий субъекта решения задачи, названных алгоритмом. Так появлялись «алгоритмы решения изобретательских задач» – АРИЗ-59, АРИЗ-61, АРИЗ-64 и т.д. [7–9 и др.]. Однако если бы использование предлагаемых алгоритмов привело к ощутимым результатам, то творческая задача превратилась бы в обычную, по выражению известного специалиста по проблемам составления и решения задач А.И. Павленко, «рутинную» задачу [10, с. 55]. В таком случае пришлось бы отказаться от самого понятия «творческая задача», действия по решению которой, как пишет И.Я. Лернер, не детерминируются или не полностью (неоднозначно) детерминируются какими-либо предписаниями, т.е. если решающему неизвестен алгоритм решения и необходимо осуществить поиск, шаги которого заранее не даны [11, с. 81]. Процесс решения творческих задач требует от субъекта нестандартных подходов, хотя и осуществляется на основе знакомого ему материала естественно-математических и технических наук. Уже не нужно доказывать, что систематические упражнения учащихся в решении таких задач способствуют развитию их творческих способностей.
Вместе с этим наши исследования позволили прийти к выводу, что наивысшим уровнем творчества человека является все же не умение решать нестандартные задачи, которые ставятся перед ним в готовом виде, а умение ощущать, видеть, выявлять в окружающем мире дисгармонию, несогласованность в действиях отдельных элементов определенной системы (далее все это будем называть дисгармонией), умение формулировать проблему, умение выявлять противоречия между отдельными элементами системы с последующей постановкой на основе этого задачи и ее решением. Если задача сформулирована правильно, то для получения ответа (выполнения ее требования) требуется не так и много.
Почему к такому выводу пришли не сразу, объяснить непросто. Вероятно, одной из причин является то, что мы живем под влиянием сформированной в первые годы обучения в школе психологической установки: задачи существуют в готовом виде («готовые» задачи). Над их происхождением мы задумываемся не сразу. Если это учебные задачи, то их составляют люди, которые имеют отношение к процессу обучения. Если эти люди сведущи в определенной области производства, то они могут составить задачи, которые отражают ее характер. Гак появляются задачи с техническим, биологическим и другим содержанием. Учителя и ученики умеют составлять обратные задачи к уже существующим. При этом задача больше воспринимается как средство обучения, а не как его хотя бы отдаленная цель.
На основе этих соображений становятся понятными безуспешные попытки получить для решения реальные оригинальные, но «чужие» задачи. Будучи руководителем школьного кружка юных изобретателей и рационализаторов, автор несколько раз обращался в соответствующие службы некоторых местных заводов с просьбой дать кружковцам задачи, которые они не могут решить самостоятельно (как это было наивно!). Нас знакомили с задачами тематических планов по изобретательству и рационализаторству. Тем не менее, когда через определенное время мы приносили решения некоторых из них, нам вежливо объясняли, что эти задачи уже решены и люди ждут за это вознаграждение. Автор считал, что с ним и его учениками ведется какая-то нечестная игра. С целью успокоения принял для себя такую версию: в темник (так на заводах называли упомянутый выше тематический план) включаются лишь те задачи, которые уже имеют решения (план не мог не выполняться, ведь под него закладывались немалые средства), т.е. существует определенная подстраховка. Однако со временем стала понятной и другая сторона дела: никто не хочет отдавать другому человеку выявленную им проблему, тем более проблему, которая уже доведена им до уровня задачи. Решение задачи – это всего-навсего незначительное, но наиболее заметное извне проявление последнего элемента цепочки: дисгармония – проблема – противоречие – задача.
Сначала человек должен обнаружить в окружающем мире дисгармонию. Но, чтобы сделать это, нужно уметь ощущать гармонию. Вряд ли сможет, например, музыкант, который не ощущает гармонию звуков, найти фальшь в исполняемом музыкальном произведении. Поэтому выявлять дисгармонию может лишь тот человек, который достиг уровня ощущения в ней гармонии.
Такое человеческое качество, как видение, зоркость или ощущение проблем [12], – достаточно редкий дар. Найти для себя никем еще не разрешенную проблему – это, наверное, один из важнейших пунктов деятельности ученого и изобретателя. Вспомним канадского ученого Ганса Селье, который всю жизнь исследовал стресс [13], нашего соотечественника Нурбея Владимировича Гулиа – создателя маховичних аккумуляторов [14] и многих других.
То, что людей с названным качеством не так уже много, мы ощущаем во время разработки задач для турниров и конкурсов. Задачи предлагают в основном одни и те же люди. И, как только удастся сформулировать и «засветить» интересную задачу, она сразу приобретает второе, а затем и третье дыхание – становится задачей аналогичного конкурса, который проводится в другом государстве, темой для научно-исследовательской работы члена Малой академии наук (МАН), дипломной работы выпускника вуза и т.п. Чтобы в этом убедиться, достаточно проанализировать работы участников всеукраинских конкурсов – защит научно-исследовательских работ членов МАН Украины последних лет, задачи турниров юных физиков и турниров юных изобретателей и рационализаторов. Между прочим, далеко не все, кто использует «чужую» проблему, упоминают в своей работе ее автора. Если не учитывать существующее при этом нарушение прав человека на интеллектуальную собственность, то остается одно: решение задачи в их понимании оценивается намного выше, чем поставленная (другим человеком) и доведенная до уровня задачи проблема. При этом, конечно, имеются в виду не любые проблемы, а лишь те из них, решение которых может принести реальную пользу людям.
Рассмотрим цепочку дисгармония – проблема – противоречие – задача на конкретном примере.
Есть люди, которым нравится подолгу сидеть за чашкой чая или кофе. Напиток они употребляют небольшими порциями. К сожалению, он достаточно быстро остывает. Мы обратили внимание на существующее неудобство, которое можно условно назвать дисгармонией.
Упомянутое неудобство (дисгармонию) замечают практически все люди, но далеко не каждый из них способен к ее актуализации и последующему отражению в виде конкретной проблемы: было бы неплохо, если бы температура жидкости в течение продолжительного времени не опускалась ниже допустимой.
Вместе с тем проблема еще не является задачей. В условии задачи, кроме сформулированной проблемы, должны содержаться противоречия, устранение которых и будет ее решением – выполнением здесь же поставленного требования (достижением ожидаемого эффекта). Здесь же могут быть заложены определенные ограничения. Покажем это на примере.
Задача 1. «Аккумулятор тепла». Налитая в чашку жидкость (например, чай, кофе или молоко) сначала может быть достаточно горячей (90– 100 °С), что не позволяет принимать ее без вреда для здоровья человека, а через 10–15 минут ее температура может снизиться до 40 – 50 °С, когда она воспринимается как холодная. Предложите такой вариант решения задачи, которым бы обеспечивалось поддержание температуры указанной жидкости в течение значительного промежутка времени (хотя бы около 30 мин) без потребления энергии извне.
Очевидно, что одним из противоречий в данной задаче является то, что температура жидкости, при которой ее можно употреблять человеку, держится меньший промежуток времени, чем нам бы этого хотелось. Оно отображает дисгармонию, т.е. вытекает из нее.
Существует и еще одно противоречие. Оно внесено в условие искусственно и состоит в том, что нужную температуру воды можно было бы поддерживать с помощью определенного нагревателя, например, поставить сосуд с жидкостью на кружок электроплитки. Однако в условии задачи оговорено ограничение: обеспечивать поддержание температуры жидкости в течение значительного промежутка времени (хотя бы около 30 мин) без потребления энергии извне. Как будет показано ниже, именно это противоречие привело к красивому решению задачи.
Последнее противоречие можно преодолеть за счет использования энергии системы «чашка – жидкость». Этим выполним сформулированное в условии задачи требование: не пользоваться внешними источниками энергии. Часть тепловой энергии, нагретой до температуры кипения жидкости, сначала следует аккумулировать в самой системе, а при снижении температуры жидкости до критического уровня, аккумулированную энергию необходимо использовать для ее подогревания. Остается лишь найти вещество, способное аккумулировать тепловую энергию. Для этого достаточно владеть материалом физики VIIIкласса.
Решение. Разместим между двойными стенками чашки кристаллическое вещество с температурой плавления и кристаллизации 70 – 80 °С (см. рис). Процесс остывания налитого в чашку кипятка (по сравнению с аналогичным процессом, который бы происходил в обычной чашке) значительно ускоряется в связи с тем, что определенное количество внутренней энергии воды будет тратиться еще и на плавление кристаллического вещества.
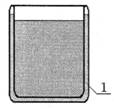
Аккумулятор тепла:
1 – кристаллическое вещество
Спустя некоторое время часть внутренней энергии всей системы передается окружающей среде. Настанет момент кристаллизации «рабочего» вещества (при температуре кристаллизации!), и часть той энергии, которая будет им выделяться, пойдет на поддержание температуры воды. Эффект достаточно впечатляющий. Если, например, в обычную чашку налить 200 г воды, взятой при температуре 100 °С, то до 50–60 °С ее температура монотонно спадет за 10–15 мин. Диапазон температур, при котором человек может употреблять чай, кофе или горячее молоко, находится в пределах 50–75 °С (это, конечно, зависит от субъекта). Это означает, что промежуток времени, в течение которого он может употреблять напиток из обычной чашки, длится 5–8 мин. Если же воспользоваться предлагаемой нами чашкой, то этот промежуток времени значительно увеличивается. (Данный аккумулятор тепла создан Павлом Давиденко.)
Конечно, нас больше впечатляет само решение задачи, а не та деятельность, которая осуществлялась перед ним. Все, что осуществляется до формулирования условия задачи, нельзя назвать процессом ее решения, ведь нельзя выполнять действия с объектом, которого просто не существует. В то время осуществляется важная творческая деятельность человека по описанной выше цепочке.
Нельзя не вспомнить описанный П.Л. Капицей эпизод, который имел место во время его пребывания в Кембриджском университете. Некий молодой ученый, который закончил университет и два года проработал над кандидатской диссертацией, подошел к Эрнесту Резерфорду с такими словами: «Вот я защитил свою кандидатскую работу, что мне теперь делать дальше?» Резерфорд ему ответил: «Бросить заниматься наукой. Если после двух лет самостоятельной работы вы не знаете сами, что вам делать дальше, значит, из вас ученого не выйдет» [15]. Вполне понятно, что великий Резерфорд не увидел в этом человеке того, кто способен к ощущению и выявлению дисгармонии, которая содержится в знаниях людей о природе, к умению формулировать проблемы, обнаруживать противоречия между отдельными физическими явлениями, что дает возможность формулировать собственные задачи. Это довольно четко проявляется в ходе развития физической теории [16].
Ранее уже отмечалось, что существуют определенные приемы, использование которых способствует поиску решений некоторых типов творческих задач. Мы умеем также организовывать учебную деятельность, которая направлена на овладение данными приемами. Иначе говоря, мы умеем развивать способности человека к творчеству, которое состоит в решении тех творческих задач, которые он получает в «готовом» виде. Вместе с тем мы еще имеем определенные трудности в развитии тех способностей, которые разрешали бы человеку начинать творчество из обнаружения дисгармонии. Этому и будут посвящены дальнейшие исследования автора.
1. Разумовский, В. Г. Развитие творческих способностей учащихся в процессе обучения физике : пособие для учителей. – М. : Просвещение, 1975. – 272 с.
2. Разумовский, В. Г. Творческие задачи по физике в средней школе. – М. : Просвещение, 1966. – 154 с.
3. Давиден, А. А. Изобретательские задачи в школьном курсе физики : пособие для учителей. – Чернигов : Десн. правда, 1996. – 96 с.
4. Альтов, Г. С. И тут появился изобретатель : научно-популярная книга. – М. : Дет. лит., 1984. – 126 с.
5. Пархоменко, В. П. Основы технического творчества : учеб. пособие. – Мн. : Адукацыя iвыхаванне, 2000. – 148 с.
6. Альтшуллер, Г. С. Дерзкие формулы творчества // Дерзкие формулы творчества / сост. А. Б. Селюцкий. – Петрозаводск : Карелия, 1987. – С. 13 – 81.
7. Альтшуллер, Г. С. Алгоритм изобретения. – М. : Московский рабочий, 1969. – 272 с.
8. Альтшуллер, Г. С. Найти идею. Введение в теорию решения изобретательских задач. – Новосибирск : Наука, 1986. – 209 с.
9. Альтшуллер, Г. С. Творчество как точная наука. – М.: Советское радио, 1979. – 176 с.
10. Павленко, А. I. Методика навчання учнiв середньоiшколи розв'язуванню iскладанню фiзичних задач: навчально-методичний посiбник. – Запорiжжя : Прем'ер, 2000. – 102 с.
11. Лернер, И. Я. Дидактические основы методов обучения. – М.: Педагогика, 1981. – 186 с.
12. Лук, А. Н. Творчество // Наука и жизнь. – 1973. – № 1. – С. 76–80; № 2. – С. 79–83.
13. Селъе, Г. От мечты – к открытию: как стать ученым : пер. с англ. – М.: Прогресс, 1987. – 368 с.
14. Гулиа, Н. В. В поисках «энергетической капсулы». – М.: Дет. лит., 1986. – 143 с.
15. Капица, П. Л. Изучать физику с точки зрения научного работника // Эксперимент. Теория. Практика. – М.: Наука, 1987. – С. 224 – 231.
16. Данин, Д. С. Вероятностный мир. – М.: Знание, 1981. – 208 с.
| Выложил | alsak |
| Опубликовано | 26.12.07 |
| Просмотров | 9835 |
| Рубрика | Экспериментальные задачи | Методика |
| Тема | Без тем |