Лобко Е.В. Формирование системной деятельности учащихся
Лобко Е.В. Формирование системной деятельности учащихся в процессе преподавания курса физики в средней школе // Фiзiка: праблемы выкладання. – 1996. – Вып. 2. – С. 42-48.
Деятельность — специфически человеческая форма активного отношения к окружающему миру, содержание которой составляет его целесообразное изменение и преобразование, (философский энциклопедический словарь. — М.: Советская энциклопедия, 1983.) Человечество за время своего развития создало огромное количество форм, видов и типов деятельности. Например, одних только профессиональных — десятки тысяч. В дальнейшем многие из них будут развиваться, изменяться, возникнут новые. Но это проблемы профессиональных учебных заведений.
Основная сложность обучения учащихся возникает из-за того, что большинство из них не определились, какой деятельностью они будут заниматься в жизни. Поэтому средняя школа должна научить таким формам и видам деятельности, которые можно применять практически в любой жизненной ситуации.
Каждый предмет в соответствующем классе средней школы имеет свои возможности в обучении деятельности. Если проанализировать курс физики в средней школе, то есть возможность использовать его для обучения системной деятельности. Она основана на системном познании мира. (Аверьянов А.Н. Системное познание мира. — М.: Политиздат, 1985.) Исходя из возможностей курса физики, системную деятельность можно поэтапно представить в следующих формах; линейной, плоскостной, спиральной, объемной. Есть и другие формы, но пока реально осуществимы в наших условиях первые две. Рассмотрим их более подробно.
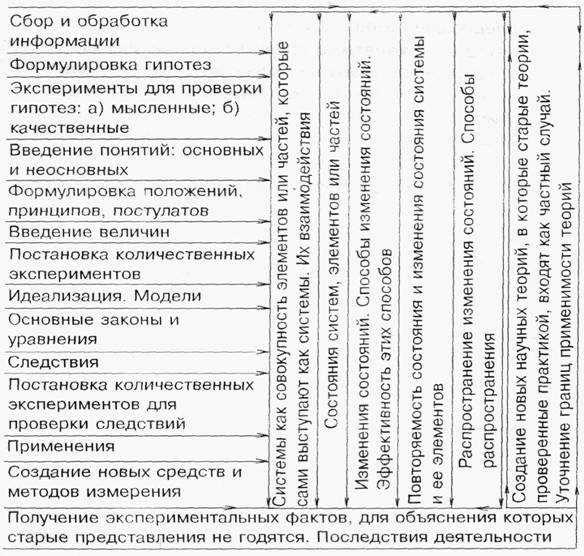
Линейная форма системной деятельности (схема 1) формируется через существующие программы, учебные пособия, содержимое учебного материала, а также соответствующие этапы, формы, методы, систему и организацию занятий в процессе изучения физики. Поэтапное введение подобных форм позволяет наряду с известными подходами в обучении учащихся в средней школе использовать и новые. Мы выделяем следующие этапы. Первый — физика в VII и VIII классах. Второй — физика в IX классе (раздел «Механика»). Третий — классическая физика в X и XI классах. Четвертый — элементы современной физики в XI классе. Перед каждым этапом с учетом знаний и умений учащихся используется форма, соответствующая их уровню и возможностям.
Схема 1. Линейная форма системной деятельности
|
Наблюдения за: системами, элементами или частями системы, их состоянием и изменением состояния, способами изменения состояния, повторяемостью состояний и изменений состояний, способами распространения состояния и изменения состояния и пр. |
|
Формулировка гипотез |
|
Эксперименты для проверки гипотез: мысленные, качественные |
|
Введение понятий: основных и неосновных |
|
Формулировка положений, принципов, постулатов |
|
Введение величин |
|
Постановка количественных экспериментов |
|
Идеализация — чем и в каких условиях пренебрегаем. Модели |
|
Основные законы и уравнения |
|
Следствия |
|
Постановка количественных экспериментов для проверки следствий |
|
Применения |
|
Последствия деятельности |
|
Разработка и создание новых приборов и методов измерения |
|
Получение новых экспериментальных фактов, для объяснения которых старые представления не годятся |
|
Создание новой научной теории, в которую старая входит как частный случай |
|
Уточнение границ применимости понятий, представлений, положений, принципов, постулатов, законов, уравнений и всей теории в целом. Достоинства и недостатки теорий |
Линейная форма системной деятельности (см. схему 1) вводится в начале системной деятельности третьего этапа. Нами применяются следующие методы обучения.
1. Метод неоднократного представления, изучения, повторения, обобщения и систематизации знаний и умений учащихся. Он позволяет на каждом занятии или системе занятий решать комплекс взаимосвязанных педагогических проблем: обучать, развивать, воспитывать и формировать научное мышление.
2. Метод последовательного изучения, повторения, обобщения и систематизации знаний и умений учащихся. При этом методе изучения учебный материал курса физики в IX - XI классах также группируется в соответствии с представлением о линейной деятельности (схема 1).
3. Метод параллельного изучения, повторения, обобщения и систематизации знаний и умений. Он используется на третьем этапе. Этот метод позволяет совместно изучать, повторять, обобщать, сравнивать, объединять и систематизировать темы и разделы курса физики. Например, темы «Основы молекулярно- кинетической теории» и «Элементы термодинамики», «Электрическое поле» и «Магнитное поле», «Механические колебания» и «Электромагнитные колебания», «Механические волны» и «Электромагнитные волны».
4. Формирование единой понятийной основы: система, состояние системы и ее элементов или частей, изменение состояния, способы изменения состояния и эффективность этих способов, повторяемость состояния и изменения состояния, распространение состояний и изменений состояний, способы распространения и др. Они начинают формироваться при изучении в IX классе тем «Законы сохранения» и «Механические колебания и волны» и через повторение, обобщение, систематизацию тем «Основы кинематики» и «Основы динамики. Элементы статики». На их материале формируются следующие понятия: механические системы, их элементы или части, взаимодействие между ними, механическое состояние системы, ее элементов или частей, изменение механического состояния, быстрота изменения механического состояния, эффективность способов изменения состояния, повторяемость механического состояния и изменения состояния, способы распространения изменения механического состояния. При дальнейшем изучении курса физики представления об основных понятиях расширяются й углубляются. Все эти и другие подходы, система и организация занятий позволяют в начале четвертого этапа через обобщение и систематизацию классической физики сформировать плоскостную форму системной деятельности. В свернутом виде ее можно представить с помощью схемы 2. В этой схеме стрелки →, ←, ↑, ↓ указывают направления деятельности соответственно влево, вправо, вверх, вниз.
Схема 2. Плоскостная форма системной деятельности
5. Большую роль в формировании системной деятельности играет решение задач в школе и дома с использованием разработанных на основе системного подхода рекомендаций. Приведем одну из них. Она предлагается учащимся в начале третьего этапа.
ПОРЯДОК ДЕЯТЕЛЬНОСТИ
ПРИ РЕШЕНИИ ФИЗИЧЕСКИХ ЗАДАЧ
I. Анализ условия задачи
1. Несколько раз внимательно прочитайте условие задачи.
2. Представьте, о чем говорится и подразумевается в этом условии;
а) выясните значение непонятных выражений;
б) представьте систему, ее элементы и явления, которые происходят или могут происходить;
в) изобразите схематически на рисунке систему и ее строение, выяснив, из каких элементов или частей она состоит, сколько их, как и с помощью чего они взаимодействуют. Вспомните, какими величинами характеризуется система, характер взаимодействия и действие одного тела на другое и какие из них известны по условию задачи;
г) обратите внимание на состояние системы и представьте ее свойства в этом состоянии. Какими величинами характеризуется состояние и свойства? Какие из них даны?
д) выясните, происходит ли изменение строения, состояния и свойства системы со временем. Сколько состояний рассматривается и подразумевается в задаче?
е) выберите систему отсчета. Изобразите на рисунке начальное, конечное и промежуточное состояния в моменты времени, когда строение, свойства, положение и состояние системы меняются. Для каждого тела, состояния и изменения состояния введите и обозначьте на рисунке все величины, указав для векторных величин направление и точку приложения;
ж) представьте, какими способами изменяются состояния. Введите величины, характеризующие эти способы и их эффективность;
з) выясните, происходит ли повторяемость состояния и изменения состояния, распространение изменения состояния и каким способом;
и) по условию задачи сделайте предположение, какими факторами можно пренебречь и почему. Обратите внимание, есть ли элементы симметрии, антисимметрии и какие;
к) четко представьте, что необходимо найти, введите соответствующие обозначения.
3. Изобразите условие задачи с помощью графиков.
4. Запишите математические выражения законов и уравнений, с помощью которых, исходя из ваших предположений, можно решить эту задачу.
5. Прочитайте еще раз условие задачи и запишите, что дано в единицах СИ и что найти.
II. Получение решаемой системы уравнений
1. Для этого полезно убедиться в том, что число неизвестных величин равно числу независимых уравнений.
2. Чтобы получить недостающие уравнения, возможно, используя условие задачи, применить определение неизвестных величин, законы сохранения, условие непрерывности, законы Ньютона и другие уравнения и законы, связывающие неизвестные величины.
3. Имейте в виду, что при решении системы уравнений, у которой число уравнений меньше числа неизвестных, как это часто бывает, лишняя величина может сократиться в процессе алгебраических преобразований.
III. Решение системы уравнений относительно искомой величины
1. Решать систему уравнений нужно, начиная с исключения тех неизвестных величин, которые не требуется находить по условию задачи.
2. Следите за тем, чтобы при каждом алгебраическом действии число неизвестных уменьшалось.
3. Проверяйте каждое алгебраическое действие над физическими величинами с алгебраическими действиями над их единицами в СИ.
IV. Анализ полученной формулы
1. Проверьте, все ли величины, входящие в правую часть полученного выражения, даны. (Табличные значения величин должны быть записаны в «Дано» в единицах СИ.)
2. Проверьте выполнение условия равенства наименований.
3. Исследуйте предельные и частные случаи, для которых значение искомой величины очевидно.
4. Используя физический смысл искомой величины и условие задачи, попробуйте предсказать приблизительно результат вычисления величины или укажите границы этого результата.
V. Вычисление искомой величины
1. Для получения результата проведите арифметические расчеты, используя правила приближенных вычислений, и сравните их с предсказанными значениями.
2. Окончательное значение получите с помощью микрокалькулятора (с соответствующей степенью точности).
VI. Анализ численного значения
Он не должен противоречить физическому смыслу, условию задачи и точности данных физических величин.
VII. Решите задачу при помощи другой теории или других методов
VIII. Сравните результат и запишите ответ в стандартной форме
Если в основу концепции образования в Республике Беларусь положить принцип деятельности, не только не теряются предыдущие успехи, но и достигается качественно новый уровень образования, особенно при переходе к 12-летнему обучению в средней школе. Уверенность автора основана на том, что с использованием этого принципа решаются многие проблемы образования: преемственность и непрерывность; межпредметные связи; объективность оценки деятельности ученика, студента, класса, группы, учителя, школы, вуза и т.д.
| Выложил | alsak |
| Опубликовано | 31.12.09 |
| Просмотров | 7208 |
| Рубрика | Методика | Решение задач |
| Тема | Без тем |