Петрович Г.И. О порядке главных максимумов от дифракционной решётки в ЦТ
-
2.3/5 оценка (6 голосов)
Петрович Г. И. О порядке главных максимумов от дифракционной решётки в решениях задач централизованного тестирования // Фiзiка: праблемы выкладання. – 2009. – № 3. – С. 34-40.
При перпендикулярном (нормальном) падении параллельного пучка монохроматического света на дифракционную решётку на экране в фокальной плоскости собирающей линзы, расположенной параллельно дифракционной решётке, наблюдается неоднородная картина распределения освещённости разных участков экрана (дифракционная картина).
Главные максимумы этой дифракционной картины удовлетворяют следующим условиям:
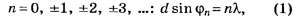
где n — порядок главного дифракционного максимума, d — постоянная (период) дифракционной решётки, λ— длина волны монохроматического света, φn— угол между нормалью к дифракционной решётке и направлением на главный дифракционный максимум n-го порядка.
Постоянная (период) дифракционной решётки длиной l

где N — количество щелей (штрихов), приходящихся на участок дифракционной решётки длиной I.
Наряду с длиной волны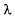 часто используется частота v волны.
часто используется частота v волны.
Для электромагнитных волн (света) в вакууме

где с = 3 *108 м/с — скорость распространения света в вакууме.
Выделим из формулы (1) наиболее трудно математически определяемые формулы для порядка главных дифракционных максимумов:
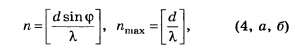
где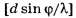 обозначает целую часть числа d*sin(φ/λ).
обозначает целую часть числа d*sin(φ/λ).
Недоопределённые аналоги формул (4, а,б) без символа [...] в правых частях содержат в себе потенциальную опасность подмены физически обоснованной операции выделения целой части числа 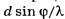 операцией округления числа d*sin(φ/λ) до целочисленного значения по формальным математическим правилам.
операцией округления числа d*sin(φ/λ) до целочисленного значения по формальным математическим правилам.
Подсознательная тенденция (ложный след) подмены операции выделения целой части числа d*sin(φ/λ) операцией округления
этого числа до целочисленного значения по математическим правилам ещё более усиливается, когда речь идёт о тестовых заданиях типа В на определение порядка главных дифракционных максимумов.
В любых тестовых заданиях типа В численные значения искомых физических величин по договорённости округляются до целочисленных значений. Однако в математической литературе нет единых(го) правил(а) округления чисел.
В справочной книге В. А. Гусева, А. Г. Мордковича по математике для учащихся [1] и белорусском учебном пособии Л. А. Латотина, В. Я. Чеботаревского по математике для IV класса [2] приводятся по существу одни и те же два правила округления чисел. В [1] они сформулированы так: "При округлении десятичной дроби до какого-нибудь разряда все следующие за этим разрядом цифры заменяются нулями, а если стоят после запятой, то их отбрасывают. Если первая следующая за этим разрядом цифра больше или равна пяти, то последнюю оставшуюся цифру увеличивают на 1. Если же первая следующая за этим разрядом цифра меньше 5, то последнюю оставшуюся цифру не изменяют".
В справочнике М. Я. Выгодского по элементарной математике [3], выдержавшем двадцать семь (!) изданий, написано (с. 74): "Правило 3. Если отбрасывается цифра 5, а за ней нет значащих цифр, то округление производится до ближайшего чётного числа, т.е. последняя сохраняемая цифра остаётся неизменной, если она чётная, и усиливается (увеличивается на 1), если она нечётная".
Ввиду существования различных правил округления чисел следовало бы правила округления десятичных чисел явно сформулировать в "Инструкции для учащихся", прилагаемой к заданиям централизованного тестирования по физике. Это предложение приобретает дополнительную актуальность, так как в белорусские вузы поступают и проходят обязательное тестирование не только граждане Беларуси и России, но и других стран, и заведомо неизвестно, какими правилами округления чисел они пользовались при обучении в своих странах.
Во всех случаях округление десятичных чисел будем производить по правилам, приведённым в [1], [2].
После вынужденного отступления, возвратимся к обсуждению рассматриваемых физических вопросов.
С учётом нулевого (n = 0) главного максимума и симметричного расположения остальных главных максимумов относительно него общее количество наблюдаемых главных максимумов от дифракционной решётки подсчитывается по формулам:
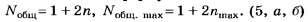
Если расстояние от дифракционной решётки до экрана, на котором наблюдается дифракционная картина, обозначить через Н, то координата главного дифракционного максимума n-го порядка при отсчёте от нулевого максимума равна
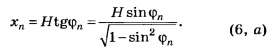
Если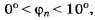 то
то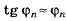 (радиан)
(радиан)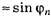 и
и
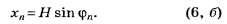
Задачи на рассматриваемую тему часто предлагают на тестированиях по физике.
Начнём обзор с рассмотрения российских тестов, использовавшихся белорусскими вузами на начальном этапе, когда тестирование в Беларуси было необязательным и проводилось отдельными учебными заведениями на свой страх и риск как альтернатива обычной индивидуальной письменно-устной форме проведения вступительных экзаменов.
Тест № 7 [4]
А32. Наибольший порядок спектра, который можно наблюдать при дифракции света с длиной волны λ на дифракционной решётке с периодом d=3,5λ равен
1) 4; 2) 7; 3) 2; 4) 8; 5) 3.
Решение
При освещении дифракционной решётки монохроматическим светом ни о каких спектрах не может быть и речи. В условии задачи речь должна идти о главном дифракционном максимуме наибольшего порядка при перпендикулярном падении монохроматического света на дифракционную решётку.
По формуле (4, б)
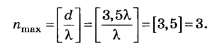
Из недоопределённого условия
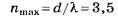
на множестве целых чисел, после округления получаем nmах=4.
Только благодаря несовпадению целой части числа d/λ с его округлённым целочисленным значением правильное решение (nmах=3) отличается от неправильного (nmax=4) на тестовом уровне.
Изумительная миниатюра, несмотря на огрехи формулировки, с филигранно выверенным по всем трём версиям округления чисел ложным следом!
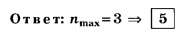
А18. Если постоянная дифракционной решётки d=2 мкм, то для нормально падающего на решётку белого света 400 нм <λ< 700 нм наибольший полностью наблюдаемый порядок спектра равен
1)1; 2)2; 3)3; 4)4; 5)5.
Решение
Очевидно, что nсп=min(n1max, n2max)
По формуле (4, б)
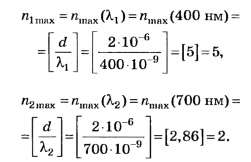
Округляя числа d/λ до целочисленных значений по правилам [1] — [3], получаем:
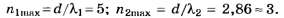
Благодаря тому, что целая часть числа d/λ2 отличается от его округлённого целочисленного значения, данное задание позволяет на тестовом уровне объективно отличить правильное решение (nсп=2) от неправильного (nсп=3). Прекрасная задача с одним ложным следом!
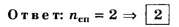
ЦТ 2002 г. Тест № 3 [5]
В5. Найдите наибольший порядок спектра для жёлтой линии Na (λ= 589 нм), если постоянная дифракционной решётки d = 2 мкм.
Решение
Задание сформулировано научно некорректно. Во-первых, при освещении дифракционной решётки монохроматическим светом, как уже отмечалось выше, не может быть и речи о спектре (спектрах). В условии задачи речь должна идти о наибольшем порядке главного дифракционного максимума.
Во-вторых, в условии задания должно быть указано, что свет падает нормально (перпендикулярно) на дифракционную решётку, ибо только этот частный случай рассматривается в курсе физики средних общеобразовательных учреждений. Считать это ограничение подразумевающимся по умолчанию нельзя: в тестах все ограничения должны быть указаны явно! Тестовые задания должны представлять собою самодостаточные, научно корректные задания.
С учётом вышеприведённых уточнений
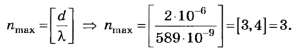
Число 3,4, округлённое до целочисленного значения по правилам арифметики [1] — [3], также даёт 3. Именно поэтому данное задание следует признать простым и, по большому счёту, неудачным, так как на тестовом уровне оно не позволяет объективно различить правильное решение, определяемое по целой части числа 3,4, от неправильного решения, определяемого по округлённому целочисленному значению числа 3,4. Различие обнаруживается только при подробном описании хода решения, что и сделано в данной статье.
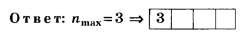
Дополнение 1. Решите вышеприведённую задачу, заменив в её условии d=2 мкм на d=1,6 мкм. Ответ: nmax = 2.
ЦТ 2002 г. Тест 4 [5]
В5. На дифракционную решётку направляется свет от газоразрядной лампы. На экране получаются дифракционные спектры излучения лампы. Линия с длиной волны λ1= 510 нм в спектре четвёртого порядка совпадает с линией длины волны λ2 в спектре третьего порядка. Чему равна λ2(в [нм])?
Решение
В данной задаче основной интерес представляет не решение задачи, а формулировка её условия.
При освещении дифракционной решётки немонохроматическим светом(λ1, λ2) вполне естественно говорить (писать) о дифракционных спектрах, которых в принципе нет при освещении дифракционной решётки монохроматическим светом.
В условии задания следовало бы указать, что свет от газоразрядной лампы падает нормально на дифракционную решётку.
Кроме того, следовало бы изменить филологический стиль третьего предложения в условии задания. Режет слух оборот "линия с длиной волны λ'', его можно было бы заменить на "линия, соответствующая излучению длиной волны λ'' или на более краткий — "линия, соответствующая длине волны λ''.
Формулировки тестов должны быть научно корректными и литературно безупречными. Тесты формулируют совсем не так, как исследовательские и олимпиадные задачи! В тестах всё должно быть точно, конкретно, однозначно.
С учётом приведённого уточнения условия задания имеем:
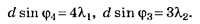
Так как по условию задания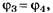 то
то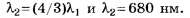
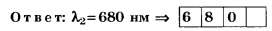
ЦТ 2002 г. Тест № 5 [5]
В5. Найдите наибольший порядок дифракционного максимума для жёлтой линии натрия с длиной волны 5,89·10-7 м, если период дифракционной решётки равен 5 мкм.
Решение
По сравнению с заданием В5 из теста № 3 ЦТ 2002 г. данное задание сформулировано точнее, тем не менее в условии задания речь следовало бы вести не о "дифракционном максимуме", а о "главном дифракционном максимуме".
Наряду с главными дифракционными максимумами всегда имеются ещё и вторичные дифракционные максимумы [6, с. 617, 618]. Не объясняя этого нюанса в школьном курсе физики, тем более надо строго соблюдать сложившуюся научную терминологию и вести речь только о главных дифракционных максимумах.
Кроме того, следовало бы указать, что свет падает нормально на дифракционную решётку.
С учётом вышеприведённых уточнений
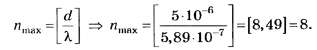
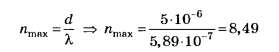
по правилам математического округления числа 8,49 до целочисленного значения опять же получаем 8. Поэтому данное задание, как и предыдущее, следует признать неудачным.
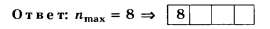
Дополнение 2. Решите вышеприведённое задание, заменив в его условии d=5 мкм на (1=А мкм. Ответ: nmax=6.)
Пособие РИКЗ 2003 г. Тест № 6 [7]
В5. Если второй дифракционный максимум находится на расстоянии 5 см от центра экрана, то при увеличении расстояния от дифракционной решётки до экрана на 20% этот дифракционный максимум будет находиться на расстоянии ... см.
Решение
Условие задания сформулировано неудовлетворительно: вместо "дифракционный максимум" надо "главный дифракционный максимум", вместо "от центра экрана" — "от нулевого главного дифракционного максимума".
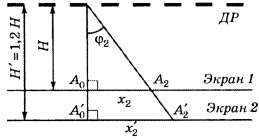
Как видно из приведённого рисунка,
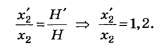
Отсюда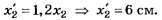
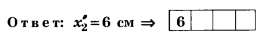
Пособие РИКЗ 2003 г. Тест № 7 [7]
В5. Определите наибольший порядок спектра в дифракционной решётке, имеющей 500 штрихов на 1 мм, при освещении её светом с длиной волны 720 нм.
Решение
Условие задания сформулировано крайне неудачно в научном отношении (см. уточнения заданий № 3 и 5 из ЦТ 2002 г.).
Есть претензии и к филологическому стилю формулировки задания. Вместо словосочетания "в дифракционной решётке" надо было бы использовать словосочетание "от дифракционной решётки", а вместо "свет с длиной волны" — "светом, длина волны которого". Длина волны — не нагрузка к волне, а её основная характеристика.
С учётом уточнений
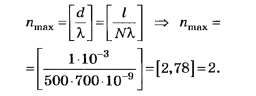
По всем трём вышеприведённым правилам округления чисел округление числа 2,78 до целочисленного значения даёт 3.
Последний факт даже при всех недостатках формулировки условия задания делает его интересным, так как позволяет на тестовом уровне различить правильное (nmax=2) и неправильное (nmax=3) решения.
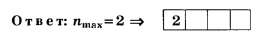
Много заданий на рассматриваемую тему содержится в ЦТ 2005 г. [8].
В условиях всех этих заданий (В1) надо добавить ключевое слово "главный" перед словосочетанием "дифракционный максимум" (см. комментарии к заданию В5 ЦТ 2002 г. Тест № 5).
К сожалению, во всех вариантах тестов В1 ЦТ 2005 г. численные значения d (l,N) и λ подобраны неудачно и всегда дают в дробях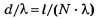
число "десятых" меньше 5, что не позволяет на тестовом уровне отличить операцию выделения целой части дроби (правильное решение) от операции округления дроби до целочисленного значения (ложный след). Это обстоятельство ставит под сомнение целесообразность использования этих заданий для объективной проверки знаний абитуриентов по рассматриваемой теме.
Похоже на то, что составители тестов увлеклись, образно говоря, приготовлением различных "гарниров к блюду", не думая об улучшении качества основной компоненты "блюда" — подборе численных значений d (l,N) и λ с целью увеличения числа "десятых" в дробях d/λ=l/(N*λ).
ЦТ 2005 г. Вариант 4 [8]
В1. На дифракционную решётку, период которой d1=1,2 мкм, падает нормально параллельный пучок монохроматического света с длиной волны λ=500 нм. Если её заменить на решётку, период которой d2=2,2 мкм, то число максимумов увеличится на ... .
Решение
Вместо "свет с длиной волны λ'' надо "свет длиной волны λ'' . Стиль, стиль и ещё раз стиль!
Так как
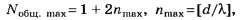
то с учётом того, что X — const, a d2>di,
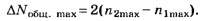
По формуле (4, б)
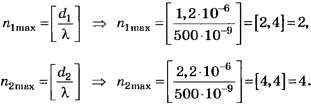
Следовательно, ΔNобщ. max=2(4-2)=4
При округлении чисел 2,4 и 4,4 до целочисленных значений тоже получаем соответственно 2 и 4. По этой причине данное задание следует признать простым и даже неудачным.
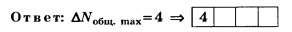
Дополнение 3. Решите вышеприведённую задачу, заменив в её условии λ=500 нм на λ=433 нм (синяя линия в спектре водорода).
ЦТ 2005 г. Вариант 6
В1. На дифракционную решётку с периодом d= 2 мкм падает нормально параллельный пучок монохроматического света с длиной волны λ=750 нм. Количество максимумов, которые можно наблюдать в пределах угла а=60°, биссектриса которого перпендикулярна плоскости решётки, равно ... .
Решение
Словосочетание "света с длиной волны λ" уже обсуждалось выше в ЦТ 2005 г., вариант 4.
Второе предложение в условии данного задания можно было бы упростить и записать так: "Количество наблюдаемых главных максимумов в пределах угла а = 60°" и далее по тексту исходного задания.
Очевидно, что
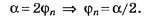
По формуле (4, а)
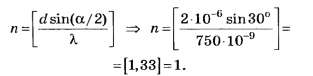
По формуле (5, а)
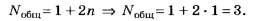
Это задание, как и предыдущее, не позволяет на тестовом уровне объективно определить уровень понимания обсуждаемой темы абитуриентами.
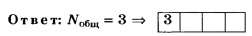
Дополнение 4. Выполните вышеприведённое задание, заменив в его условии λ=750 нм на λ= 589 нм (жёлтая линия в спектре натрия). Ответ: No6щ=3.
ЦТ 2005 г. Вариант 7
В1. На дифракционную решётку, имеющую N1- 400 штрихов на l=1 мм длины, падает параллельный пучок монохроматического света с длиной волны λ=400 нм. Если её заменить решёткой, имеющей N2=800 штрихов на l=1 мм длины, то количество дифракционных максимумов уменьшится на ... .
Решение
Опустим обсуждение неточностей формулировки задания, так как они те же, что и в предыдущих заданиях.
Из формул (4, б), (5, б) следует, что

Следовательно,
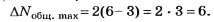
Комментарии о качестве данного задания опустим, "рука... колоть устала"!
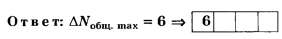
Дополнение 5. Решите вышеприведённую задачу, заменив в её условии λ=400 нм на λ=461 нм (голубая линия в спектре стронция). Ответ: ∆N=6.
ЦТ 2005 г. Вариант 8
В1. На дифракционную решётку с d=1 мкм падает нормально параллельный пучок монохроматического света. Если длина волны света λ=400 нм, то число максимумов, которые образует эта решётка, равно ... .
Решение
Злополучное "с" уже перекочевало от "света с длиной волны" к "решётке с d=1 мкм". Появилось и новое жаргонное выражение — "число максимумов, которые образует эта решётка". Сама по себе "решётка" не образует дифракционной картины, поэтому следовало бы написать "количество главных максимумов, образованных освещённой решёткой, равно...".
По формулам (5, б), (4, б)
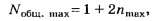
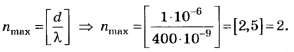
По версии округления чисел [1], [2] целочисленное значение числа 2,5 равно 3, а по версии М. Я. Выгодского [3] — 2.
В сравнении с российским заданием А32 из № 7 Тестов по физике [4], которое рассмотрено выше, данный белорусский тест является ущербным, но на фоне белорусских тестов ЦТ 2005 г. на рассматриваемую в данной статье тему он является лучшим, несмотря на неточности его формулировки.
Итак, Nобщ. max=1+2*2=5 а по версии округления чисел [1], [2] Nобщ. max= 1+2*3 =7 (ложный след).
Благодаря этому ложному следу, данное задание в рамках версии округления чисел [1], [2] позволяет на тестовом уровне отличить правильное решение (Nобщ. max=5) от неправильного (Nобщ. max=7).
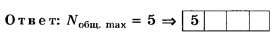
ЦТ 2008 г. Вариант 1 [9]
В12. На дифракционную решётку нормально падает параллельный пучок монохроматического света длиной волны λ=720 нм. Если период решётки d = 5 мкм, то максимальный порядок kmax дифракционного спектра ... .
Решение
Задание сформулировано научно некорректно (см. условия предыдущих заданий), но численные значения величин d и λ подобраны удачно и на тестовом уровне правильное решение, определяемое по целой части числа , отличается от неправильного решения, определяемого по округлённому целочисленному значению числа d/λ
, отличается от неправильного решения, определяемого по округлённому целочисленному значению числа d/λ
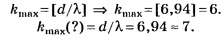
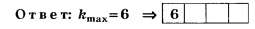
Задания В12 из других вариантов тестов ЦТ 2008 г. предлагаю читателям рассмотреть самостоятельно.
Вывод
За многие годы проведения централизованных тестирований по физике так и не созданы качественные задания на определение порядка главных дифракционных максимумов при перпендикулярном освещении дифракционной решётки монохроматическим светом: то ли условия заданий были сформулированы некорректно, то ли численные значения величин d(l, N) и X были подобраны неудачно и не позволяли на тестовом уровне отличить правильное решение от неправильного.
Список использованной литературы
1. Математика: справочные материалы: кн. для учащихся / В. А. Гусев, А. Г. Мордкович. — Москва : Просвещение, 1988.
2. Математика: учеб. пособие для 4-го класса общеобр. школы с рус. яз. обуч. / Л. А. Лату-тин, В. Д. Чеботаревский; пер. с бел. яз. Т. В. Водневой. — 2-е изд. — Минск : Нар. асвета, 2002.
3. Справочник по элементарной математике. — 27-е изд., испр. / М. Я. Выгодский. — Москва : Наука, 1986.
4. Тесты по физике. 11 кл. / Центр тестирования Министерства образования России. — Москва : Просвещение, 2001.
5. Тесты. Физика. Русский язык: варианты и ответы централизованного тестирования: пособие для подготовки к тестированию / Респ. ин-т контроля знаний. — Минск : Асар, 2003.
6. Справочник по физике для инженеров и студентов вузов. — 6-е изд., испр. / Б. М. Яворский, А. А. Детлаф. — Москва : Наука, 1974.
7. Тесты: Физика. Материалы для подготовки к централизованному тестированию / Респ. ин-т контроля знаний. — Мозырь : Белый Ветер, 2003.
8. Централизованное тестирование. Физика: сб. тестов / Респ. ин-т контроля знаний Мин-ва образования Респ. Беларусь. — Минск : Юнипресс, 2005.
9. Централизованное тестирование. Физика: сб. тестов / Респ. ин-т контроля знаний Мин-ва образования Респ. Беларусь. — Минск : Аверсэв, 2008.
| Выложил | alsak |
| Опубликовано | 02.03.12 |
| Просмотров | 169067 |
| Рубрика | Решение задач | ЦТ |
| Тема | Оптика |