Сакович А.Л. Движение под действием нескольких сил. Механика. Рекомендации по решению задач-1/2
Сакович А.Л. Движение под действием нескольких сил. Механика. Рекомендации по решению задач // Фiзiка: праблемы выкладання. – 2008. – № 5. – С. 27-34.
Авторский вариант.
При обучении учащихся решать задачи на движение тел под действием нескольких сил одним из распространенных способов является алгоритмический подход. Можно долго говорить о недостатках этого подхода, что он не развивает творческого мышления, не позволяет решать нестандартные задачи и т.п. Но от алгоритмического подхода это и не требуется, его основная задача научить всех остальных учеников решать хотя бы стандартные задачи. А это получается не всегда и не у всех.
В качестве примера можно предложить следующий алгоритм решения задач на движение тел под действием нескольких сил:
1. Сделайте чертеж. Укажите все действующие на тело силы, укажите направления скорости и ускорения.
2. Запишите второй закон Ньютона в векторном виде:
Используя один из способов решения, составьте систему уравнений. Проверьте, является ли полученная система уравнений полной. При необходимости воспользуйтесь дополнительными формулами.
3. Решите полученные уравнения.
В дальнейшем будем называть этот алгоритм сокращенным планом. Подобные алгоритмы описаны во многих методических пособиях [1, с. 121-122; 3, с. 143; 5, с. 136]. Но как показывает практика, учащиеся при решении задач по подобным планам, делают ошибки при выполнении отдельных пунктов. Поэтому считаю целесообразным использовать следующий подход:
- каждый пункт алгоритма разбить на элементарные операции и включить их в развернутый план;
- каждая элементарная операция отрабатывается отдельно, для чего можно использовать сборники задач, дидактические пособия. Некоторые операции требуют специально разработанных заданий, которые не всегда можно найти в литературе. Такие задания автор предлагает в этой статье (большинство задач на закрепление взяты из авторского дидактического пособия, которое размещено на сайте www.alsak.ru. Там же можно найти и другие задачи по данной теме.);
- по мере усвоения навыков, элементарные операции объединяются, сворачиваются (выполняются в уме). В итоге мы возвращаемся к сокращенному плану.
Выделим элементарные операции каждого пункта алгоритма.
1. Сделайте чертеж. Укажите все действующие на тело силы,укажите направления скорости и ускорения
Начнем с указания всех действующих на тело сил. Здесь учащиеся должны знать и уметь определять:
- при каком условии сила возникает;
- в результате взаимодействия с каким телом она возникает;
- куда направлена эта сила;
- как ее рассчитать (расчетную формулу).
Рассмотрим силы, которые встречаются в задачах школьного курса физики по механике.
Гравитационная сила 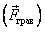 и сила тяжести
и сила тяжести 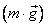
Условия возникновения. Гравитационное взаимодействие существует между всеми телами. Но при решении задач, по умолчанию (этот термин указывает, что данное действие выполняется, если нет специальных оговорок в условии.), для окружающих нас тел мы чаще всего этим взаимодействием пренебрегаем. Исключения составляют случаи, когда:
- одно из тел находится на планете (на Земле), то действует сила тяжести. В большинстве задач, по умолчанию, тела находятся на Земле, поэтому в задачах почти всегда есть эта сила;
- изучаются космические объекты (спутники, планеты, кометы и т.д.).
Результат взаимодействия с другим телом. При взаимодействии с телами больших масс (спутники, планеты, кометы и т.д.).
Определение направления силы. Гравитационная сила направлена вдоль линии, соединяющей центры масс взаимодействующих тел. Для материальных точек сила будет направлена вдоль линии, соединяющей эти точки, для сферических однородных тел – вдоль линии, соединяющей центры сфер.
Задачи на закрепление
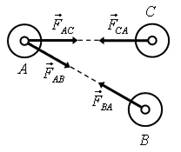
1. Два тела А и В взаимодействуют друг с другом. На рис. 1 указаны силы 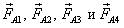 , действующие на тело A, и указаны силы
, действующие на тело A, и указаны силы 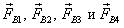 , действующие на тело B. Определите, какие из сил могли возникнуть из-за гравитационного взаимодействия двух этих тел.
, действующие на тело B. Определите, какие из сил могли возникнуть из-за гравитационного взаимодействия двух этих тел.
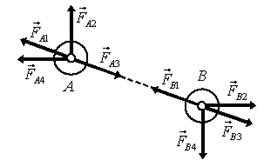
Рис. 1.
Решение. При взаимодействии возникают силы равные по величине и направлены вдоль линии, соединяющей эти тела, в противоположные стороны. Кроме того, при гравитационном взаимодействии тела притягиваются друг к другу. Поэтому в данном примере могли возникнуть только пары сил 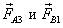 .
.
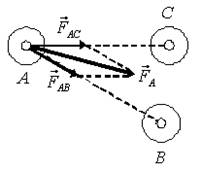
2. Три тела А, В и С притягиваются друг к другу (рис. 2). Определите направление силы гравитационного взаимодействия, действующей на тело А.
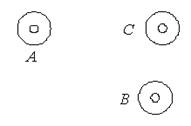
Рис. 2.
Решение. При гравитационном взаимодействии тела притягиваются друг к другу с силами, равными по величине и направленными в противоположные стороны вдоль линии, соединяющей эти тела. Тело А взаимодействует с двумя телами С и В, следовательно, на него будут действовать две силы 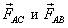 (рис. 3 а). Результирующая этих сил и укажет направление силы гравитационного взаимодействия, действующей на тело А со стороны двух тел (рис. 3 б).
(рис. 3 а). Результирующая этих сил и укажет направление силы гравитационного взаимодействия, действующей на тело А со стороны двух тел (рис. 3 б).
а б
Рис. 3.
Для расчета силы гравитационного взаимодействия используют закон всемирного тяготения 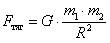 . При этом необходимо учитывать границы применимости этого закона. Данную формулу можно применять:
. При этом необходимо учитывать границы применимости этого закона. Данную формулу можно применять:
- для материальных точек;
- для сферических однородных тел;
- одно из тел материальная точка, другое – сферическое однородное тело, например, тела на Земле.
Частным видом силы всемирного тяготения является сила притяжения тел к Земле, которую называют силой тяжести ![]() . Авторы некоторых учебных пособий предлагают при определении силы тяжести учитывать вращение земли, тогда сила тяжести «определяется как геометрическая сумма действующей на тело силы гравитационного притяжения к Земле и центробежной силы инерции» [2, с. 38]. Но центробежная сила инерции во много раз меньше силы гравитационного притяжения к Земле, поэтому при решении задач ей можно пренебречь.
. Авторы некоторых учебных пособий предлагают при определении силы тяжести учитывать вращение земли, тогда сила тяжести «определяется как геометрическая сумма действующей на тело силы гравитационного притяжения к Земле и центробежной силы инерции» [2, с. 38]. Но центробежная сила инерции во много раз меньше силы гравитационного притяжения к Земле, поэтому при решении задач ей можно пренебречь.
Сила тяжести направлена вертикально вниз, к центру Земли [4, с. 222].
Задачи на закрепление
3. Определите направление силы тяжести тела А (рис. 4).
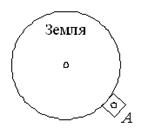
а б
Рис. 4.
Решение. Сила тяжестинаправлена вертикально вниз (рис. 5 а). Если рассматриваем планету, то сила тяжестинаправлена к центру Земли (рис. 5 б).
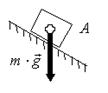
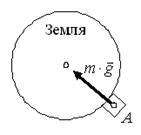
а б
Рис. 5.
Для расчета силы тяжести у поверхности Земли можно использовать формулу Fтяж = m·g. При расчетах, допускающих погрешность 1,5%, эту формулу можно применять и для тел, которые находятся на высоте меньше 100 км [4, с. 223]. В других случаях применяют формулу 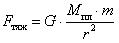 , где Mпл – масса планеты, r = Rпл + h – расстояние от центра планеты до тела, Rпл – радиус планеты, h – высота тела над поверхностью планеты.
, где Mпл – масса планеты, r = Rпл + h – расстояние от центра планеты до тела, Rпл – радиус планеты, h – высота тела над поверхностью планеты.
Сила упругости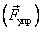
Условия возникновения. Сила упругости возникает при деформации тела. Частным видом силы упругости является:
- сила реакции опоры (сила нормального давления)
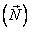 – возникает при деформации опоры под действием данного тела;
– возникает при деформации опоры под действием данного тела;
- сила натяжения подвеса
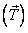 – возникает при деформации подвеса под действием данного тела.
– возникает при деформации подвеса под действием данного тела.
Результат взаимодействия с другим телом. При взаимодействии с деформированными телами (пружина, опора, подвес).
Определение направления силы. Сила упругости направлена в сторону, противоположную перемещению частей тела при его деформации. Кроме того, сила реакции опоры перпендикулярна поверхности, а сила натяжения подвеса направлена вдоль подвеса.
Задачи на закрепление
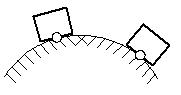
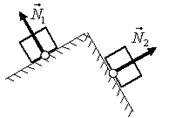
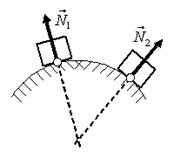
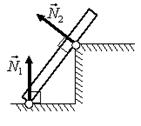
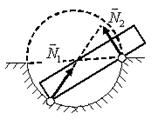
4. Укажите направление сил упругости, действующих на тела в указанных точках (рис. 6).
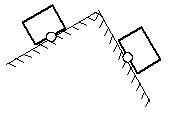
а б
в г
Рис. 6.
Решение. В данной задаче опоры деформируются под действием веса тел и частицы смещаются вниз (НО не вертикально вниз). При определении направления учтем, что:
- сила реакции опоры направлена перпендикулярно к поверхностям соприкасающихся тел против перемещения частей опоры при ее деформации;
- перпендикуляр к поверхности окружности в некоторой точке совпадает с радиусом окружности, проведенным к данной точке;
- при соприкосновении угла и поверхности перпендикуляр строим к поверхности.
Направления сил реакции опоры указаны на рис. 7.
а б
в г
Рис. 7.
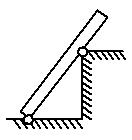
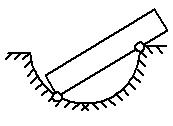
5. Укажите направление силы упругости, возникающей во вращающемся стержне в точке А (рис. 8), если в этот момент стержень: а) растягивается 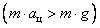 ; б) сжимается
; б) сжимается 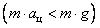 .
.
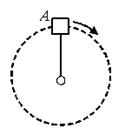
Рис. 8.
Решение. При определении направления силы упругости учтем, что она направлена вдоль оси продольно деформируемого стержня против перемещения его частей при деформации. Направления сил реакции опоры указаны на рис. 9.
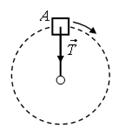
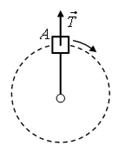
а б
Рис. 9.
Для расчета значения силы упругости используются следующие формулы:
- Fупр = k·Δl, где k – коэффициент жесткости (жесткость) тела (Н/м); Δl – абсолютное удлинение тела (м);
- Fупр = σ·S, где σ – механическое напряжение в деформированном теле (Па); S – площадь поперечного сечения тела (м2).
Если ось 0Х направить вдоль тела в сторону его растяжения, начало отсчета выбрать в точке, совпадающей с концом недеформированного тела (рис. 10), то проекцию силы упругости на ось 0Х можно рассчитать так (Fупр)x = –k·x, где х – координата конца тела. Знак «–» указывает, что сила упругости всегда противоположна по направлению абсолютному удлинению.
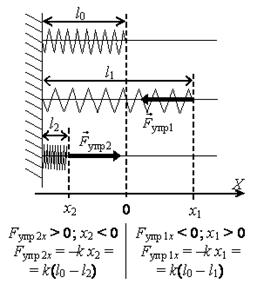
Рис. 10.
Сила трения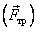
Условия возникновения. Сила сухого трения возникает при соприкосновении твердых тел. Исключением являются случаи, когда поверхности гладкие.
Если тела не движутся относительно друг друга, то между поверхностями соприкасающихся тел действует сила трения покоя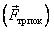 , которая уравновешивает все остальные силы, действующие на тело вдоль поверхности соприкосновения. Ее абсолютная величина может принимать любые значения от нуля до некоторого максимального Fтр п max.
, которая уравновешивает все остальные силы, действующие на тело вдоль поверхности соприкосновения. Ее абсолютная величина может принимать любые значения от нуля до некоторого максимального Fтр п max.
Если тела движутся относительно друг друга и при этом:
- одно тело скользит по поверхности другого, то между поверхностями соприкасающихся тел действует сила трения скольжения
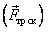 ;
;
- одно тело катится по поверхности другого, то между поверхностями соприкасающихся тел действует сила трения качения
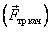 .
.
Сила сопротивления (вязкое трение) 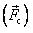 возникает при движении тел в жидкости и газе.
возникает при движении тел в жидкости и газе.
Результат взаимодействия с другим телом. При взаимодействии с твердой, не гладкой поверхностью (силы сухого трения) или с движущейся, относительно тела, жидкостью и газом (силы сопротивления).
Определение направления силы. Все силы трения направлены вдоль поверхности соприкасающихся тел. Сила трения покоя направлена в сторону, противоположную той, куда стремятся сдвинуть тело силы, действующие вдоль поверхности. Силы трения скольжения, качения, сопротивления направлены в противоположную сторону относительной скорости соприкасающихся тел.
Обратите внимание, что силы трения – это силы взаимодействия, следовательно, они всегда возникают парами. Причем эти силы приложены к взаимодействующим телам и, по третьему закону Ньютона, равны по величине и противоположны по направлению.
Задачи на закрепление
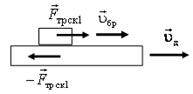
6. Определите направления сил трения, возникающих между телами (рис. 11), если: а) uбр ≠ 0, uд = 0; б) uбр = uд; в) uбр < uд. Скорости (направления и значения) заданы относительно неподвижной системы отсчета.
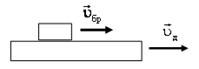
Рис. 11.
Решение. а) Так как uбр ≠ 0, uд = 0, то брусок скользит по неподвижной доске. Его скорость относительно доски направлена вправо, следовательно, сила трения скольжения, действующая на брусок, будет направлена влево. Такая же по величине, но противоположная по направлению, будет действовать сила трения на доску (рис. 12 а). Если доска не закреплена, то последняя сила будет стремиться сдвинуть доску вправо.
б) Так как uбр = uд, то брусок покоиться относительно доски, следовательно, на него действует сила трения покоя. По умолчанию, на брусок не действуют никакие другие силы вдоль поверхности, поэтому сила трения покоя будет равна нулю.
в) Так как uбр < uд, то брусок скользит по доске. Его скорость относительно доски направлена влево, следовательно, сила трения скольжения, действующая на брусок, будет направлена вправо. Такая же по величине, но противоположная по направлению, будет действовать сила трения на доску (рис.12 б).
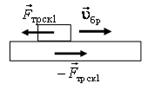
а б
Рис. 12.
7. Определите направления сил трения для тел, изображенных на рис. 13.
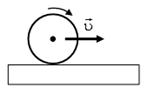
Рис. 13.
Решение. Скорость точки А колеса (рис. 14) относительно доски направлена влево, следовательно, сила трения покоя (колесо, по умолчанию, не проскальзывает), будет направлена вправо. Такая же по величине, но противоположная по направлению, будет действовать сила трения покоя на доску.
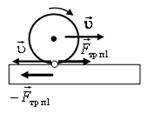
Рис. 14.
Для расчета значения сил сухого трения используются следующие формулы: Fтр пок ≤ μ·N, Fтр ск = μ·N, где коэффициенты трения покоя и скольжения считаем примерно равными.
Сила трения качения равна 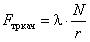 , где λ – коэффициент трения качения, r – радиус тела.
, где λ – коэффициент трения качения, r – радиус тела.
Силы сопротивления зависят от скорости, причем для малых скоростей это зависимость линейная (Fc = α·υ), для больших – квадратичная (Fc = β·υ2). Какой формулой пользоваться, обычно указано в условии задачи.
При решении задач, прежде всего, необходимо разобраться, с какими именно силами трения: покоя или скольжения, – мы имеем дело.
8. На наклонной плоскости с углом наклона α лежит брусок массой m. Коэффициент трения равен μ. Определите значение силы трения.
Решение. Вначале нужно определить о какой силе идет речь: о трении скольжения или трения покоя. Для этого надо выяснить скользит брусок по наклонной плоскости или нет. Запишем второй закон Ньютона в векторном виде 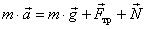 и в проекциях (рис. 15)
и в проекциях (рис. 15)
0X: m·a = m·g·sin α – Fтр, (1)
0Y: 0 = –m·g·cosα+ N. (2)
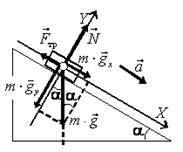
Рис. 15.
Если брусок скользит, то a > 0 (с учетом застоя) и Fтр ск = μ·N (3). Тогда с учетом (2) получаем Fтр ск = μ·m·g·cosα.
Найдем при каком условии (угле α) тело будет скользить. Подставим уравнения (2) и (3) в (1)
m·a = m·g·sin α – μ·N = m·g·sin α – μ·m·g·cos α,
a = g·(sin α – μ·cos α),
Так как a > 0, то g·(sin α – μ·cos α) > 0, sin α > μ·cos α, tg α > μ.
Следовательно, если tgα> μ, то брусок будет скользить, и сила трения будет Fтр = Fтр ск = μ·m·g·cosα.
Если tgα≤ μ, то брусок покоится (а = 0) и из уравнения (1) получаем
Fтр = Fтр п = m·g·sinα.
Архимедова (выталкивающая) сила 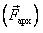
Условия возникновения. Архимедова сила действует на любое тело, погруженное в жидкость или газ, и находящееся в гравитационном поле (поле силы тяжести). Но архимедовой силой, действующей на тело, можно пренебречь, если плотность окружающей среды (жидкости или газа) во много раз меньше плотности этого тела.
Результат взаимодействия с другим телом. При взаимодействии с жидкостью или газом.
Определение направления силы. Архимедова сила направлена вертикально вверх (против направления ускорения свободного падения слоев жидкости).
Для расчета архимедовой силы применяют следующую формулу: Fарх = ρж·g·Vп/т, где ρж – плотность жидкости (или газа), в которой находится тело, Vп/т – объем погруженной части тела.
Сила тяги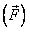
Условия возникновения. Эта сила, возникающая в работающем двигателе, или в результате действия какого-то абстрактного тела, например, «на тело действует сила F…».
Определение направления силы. Сила тяги направлена так, как указано в условии. Для двигателей, по умолчанию, эта сила направлена вдоль поверхности.
Расчетные формулы чаще всего не используются.
Таким образом в механике используются следующие виды сил:
- гравитационная сила
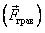 или (и) сила тяжести
или (и) сила тяжести 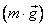 ;
;
- сила упругости
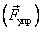 или (и) сила реакции опоры
или (и) сила реакции опоры 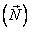 , сила натяжения подвеса
, сила натяжения подвеса 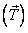 ;
;
- сила трения
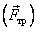 или (и) сила трения покоя
или (и) сила трения покоя 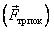 , сила трения скольжения
, сила трения скольжения 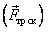 , сила трения качения
, сила трения качения 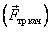 , сила сопротивления
, сила сопротивления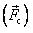 ;
;
- архимедова сила
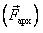 ;
;
- сила тяги
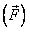 .
.
Они возникают в результате:
- взаимодействия с телами большой массы (спутники, планеты, кометы) – гравитационная сила или сила тяжести;
- взаимодействия с деформированными телами (пружина, опора, подвес) – сила упругости, сила реакции опоры, сила натяжения подвеса;
- взаимодействия с твердой, не гладкой поверхностью – силы сухого трения. Причем если тело покоится относительно поверхности – это сила трения покоя, если движется – сила трения скольжения или качения;
- движения в жидкости или газе – силы сопротивления;
- взаимодействия с жидкостью или газом, плотность которых соизмерима с плотностью тела – архимедова сила;
- работы двигателя – сила тяги.
Можно предложить несколько способов отработки элементарной операции по определению действующих сил.
1 способ. Определите, с какими другими телами взаимодействует данное тело, и введите силы, характеризующие это взаимодействие.
2 способ. Проанализируйте все перечисленные выше силы на возможность их существования в данных условиях.
Задачи на закрепление
9. Определите какие силы действуют: а) на брусок, лежащий на горизонтальном столе; б) на неподвижный воздушный шарик, закрепленный снизу к нити.
1 способ. а) Брусок взаимодействует с твердой поверхностью стола, которая под действием веса бруска будет деформироваться, с воздухом и с Землей (по умолчанию). Поэтому на брусок будут действовать: сила реакции опоры (со стороны деформированной поверхности стола) и сила тяжести (со стороны Земли). Сила трения покоя (со стороны твердой поверхностью стола) будет равна нулю, т.к. нет сил направленных вдоль поверхности стола. Архимедовой силой (со стороны воздуха) пренебрегаем, т.к. плотность воздуха во много раз меньше плотности бруска.
б) Воздушный шарик взаимодействует с воздухом, нитью, которую стремиться растянуть, и с Землей (по умолчанию). Поэтому на воздушный шарик будут действовать: архимедова сила (со стороны воздуха), сила натяжения нити (со стороны деформированной нити) и сила тяжести (со стороны Земли).
2 способ. а) Сила тяжести действует на брусок, т.к. он взаимодействует с Землей (по умолчанию); сила упругости (сила реакции опоры) действует, т.к. есть взаимодействие с деформированной поверхностью стола; сила трения (сила трения покоя) могла бы существовать из-за взаимодействия с твердой поверхностью, но нет сил направленных вдоль поверхности стола, поэтому она будет равна нулю; архимедовой силой пренебрегаем, т.к. плотность воздуха во много раз меньше плотности бруска; силы тяги нет, т.к. нет двигателя.
б) Сила тяжести действует на воздушный шарик, т.к. он взаимодействует с Землей (по умолчанию); сила упругости (сила натяжения нити) действует, т.к. есть взаимодействие с деформированной (растянутой) нитью; силы трения нет, т.к. нет взаимодействия с твердой поверхностью и нет движения в жидкости или газе; архимедова сила есть, т.к. есть взаимодействие с воздухом; силы тяги нет, т.к. нет двигателя.
Окончание следует .
| Выложил | alsak |
| Опубликовано | 12.10.08 |
| Просмотров | 30961 |
| Рубрика | Методика | Решение задач |
| Тема | Динамика |