Гребень В.М. Решение задач на экстремум с помощью неравенства Коши
Гребень В.М. Решение задач на экстремум с помощью неравенства Коши // Фiзiка: праблемы выкладання. – 1999. – № 3. – С. 100-110.
Задачи на экстремум с интересом воспринимаются учениками. Но, к сожалению, знакомятся они с ними чаще всего после прохождения в X классе производной, когда уже позади три учебных года изучения физики. Между тем для решения многих подобных задач достаточно знать и главное уметь применять сравнительно несложные неравенства. К числу таких неравенств относится прежде всего неравенство Коши. Времени на его доказательство, если ученики по какой либо причине не знакомы с ним, уходит немного, и само доказательство доступно для понимания даже восьмиклассниками.
Пусть а и b неотрицательные, т.е. a ≥ 0 и b ≥ 0, тогда можно записать ![]() или
или 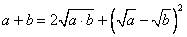 . Если отбросить
. Если отбросить 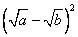 , то получим неравенство
, то получим неравенство 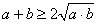 или
или 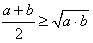 . Доказали, что среднее арифметическое двух неотрицательных a и b не меньше, чем среднее геометрическое, причем равенство достигается при а = b. Данное неравенство называют неравенством Коши. Полезно знать некоторые следствия из него.
. Доказали, что среднее арифметическое двух неотрицательных a и b не меньше, чем среднее геометрическое, причем равенство достигается при а = b. Данное неравенство называют неравенством Коши. Полезно знать некоторые следствия из него.
Произведение двух неотрицательных переменных, сумма которых постоянна, получает наибольшее значение тогда, когда эти переменные равны друг другу. Аналогично, наименьшее значение суммы двух неотрицательных переменных, произведение которых постоянно, достигается при равенстве переменных. Рассмотрим применение неравенства Коши при решении задач.
Задача 1. У продавца были весы с разными по длине плечами и гири. Для ликвидации ошибки продавец взвешивал продаваемый товар дважды, на разных чашах весов. Покупатель оплачивал среднее арифметическое значение массы. Кому это выгодно, покупателю или продавцу?
Решение. Обозначим массу товара буквой М; m1 и m2 – массы гирь, уравновешивающих товар, l1 и l2 – длины плеч.
Тогда, исходя их условия равенства моментов, получаем систему уравнений:
![]()
Из даннойсистемы легко получить
![]()
Используя неравенство Коши, можем записать
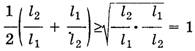 .
.
Так как в нашем случае ![]() ,
, ![]() и мы знаем, что l2 ≠ l1, то неравенство будет строгим, а поэтому
и мы знаем, что l2 ≠ l1, то неравенство будет строгим, а поэтому ![]() . Значит, покупатель заплатит за большую массу товара, чем на самом деле получит от продавца. Такая «ликвидация ошибки» более выгодна продавцу, чем покупателю.
. Значит, покупатель заплатит за большую массу товара, чем на самом деле получит от продавца. Такая «ликвидация ошибки» более выгодна продавцу, чем покупателю.
Задача 2. У продавца были весы с разными по длине плечами и гири. Но он половину веса товара отвешивал на левой чаше, а вторую половину – на правой и считал, что этим он компенсировал неточность весов. Что получалось на самом деле?
Решение. Опять на основе равенства моментов получаем систему:
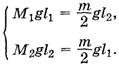
Покупатель забирал товар массой M1 + M2, а рассчитывался за товар массой m. Решая систему, получаем
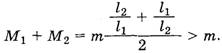
Видно, что продавец отпускал товара больше, чем оплачивал покупатель.
В связи с вышеизложенным возникает вопрос. Можно ли, пользуясь неравноплечными весами, продавать товар правильно? Для ответа перепишем систему уравнений, полученную при решении задачи 1:
![]()
Поделив одно уравнение на второе, получим пропорцию ![]() Пользуясь свойством пропорции (произведение крайних членов пропорции равно произведению средних), запишем М2 = m1·m2. Откуда
Пользуясь свойством пропорции (произведение крайних членов пропорции равно произведению средних), запишем М2 = m1·m2. Откуда 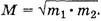 Чтобы не было обидно и покупателю и продавцу, покупателю необходимо оплачивать среднее геометрическое результата двух взвешиваний.
Чтобы не было обидно и покупателю и продавцу, покупателю необходимо оплачивать среднее геометрическое результата двух взвешиваний.
Рассмотрим две задачи, предлагавшиеся на вступительных экзаменах в МГУ.
Задача 3. Мотоциклист выезжает из пункта А и движется с постоянным ускорением 12 км/ч2 (начальная скорость равна нулю). Достигнув скорости υ, он едет с этой скоростью 25 км, а потом переходит на равнозамедленное движение, причем за каждый час скорость уменьшается на 24 км/ч, и движется так до полной остановки. Затем он стразу же поворачивает обратно и едет до пункта А с постоянной скоростью υ. При какой скорости υ мотоциклист быстрее всего проделает обратный путь от остановки до пункта А?
Решение. Длину обратного пути можно записать в виде
![]() где s2 = 25 км, а = 12 км/ч2.
где s2 = 25 км, а = 12 км/ч2.
Время, необходимое мотоциклисту для преодоления обратного пути от остановки, выражается формулой ![]() . Подставив s, получим
. Подставив s, получим
![]()
Очевидно, что своего минимума время достигает при 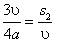 . Откуда следует, что
. Откуда следует, что
![]() .
.
Таким образом, при скорости 20 км/ч мотоциклист быстрее всего проделает обратный путь.
Задача 4. Автомобиль едет от пункта А до пункта В с постоянной скоростью 42 км/ч. В пункте В он переходит на равнозамедленное движение с ускорением а и едет так до полной остановки. Затем он сразу же начинает двигаться равноускоренно с ускорением a в первоначальном направлении. Каково должно быть значение а, чтобы через 3 часа после возобновления движения автомобиль находился ближе всего к пункту В?
Решение. Расстояние s от пункта В может быть записано в виде
![]()
где υ0 = 42 км/ч, t = 3 ч, а – ускорение.
Очевидно, что
![]()
Равенство достигается при  Откуда следует:
Откуда следует:
![]()
Итак, при ускорении 14 км/ч2 автомобиль через 3 часа после возобновления движения будут ближе всего находиться к пункту В.
Задача 5. На одном из концов соломинки, лежащей на гладкой горизонтальной плоскости, сидит кузнечик. С какой наименьшей скоростью он должен прыгнуть, чтобы попасть на другой конец соломинки? Длина соломинки l, ее масса m, масса кузнечика М.
Решение. Начальную скорость 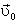 прыгнувшего кузнечика можно разложить на две составляющие: на горизонтальную
прыгнувшего кузнечика можно разложить на две составляющие: на горизонтальную 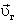 и вертикальную
и вертикальную 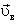 . Пусть
. Пусть 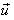 — скорость соломинки, когда кузнечик находится в полете.
— скорость соломинки, когда кузнечик находится в полете.
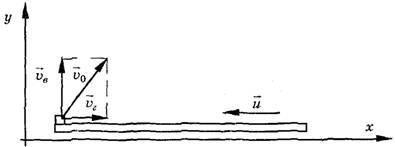
Так как трение между соломинкой и плоскостью стола отсутствует, то можно воспользоваться законом сохранения импульса: 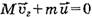 , потому что перед прыжком система, состоящая их кузнечика и соломинки, покоилась. Спроектировав скорости на ось Ох, выразим модуль скорости соломинки через модуль горизонтальной составляющей скорости кузнечика
, потому что перед прыжком система, состоящая их кузнечика и соломинки, покоилась. Спроектировав скорости на ось Ох, выразим модуль скорости соломинки через модуль горизонтальной составляющей скорости кузнечика 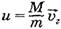 . К моменту приземления кузнечика соломинка и кузнечик, двигаясь навстречу друг другу, должны пройти по горизонтали длину соломинки l, т.е.
. К моменту приземления кузнечика соломинка и кузнечик, двигаясь навстречу друг другу, должны пройти по горизонтали длину соломинки l, т.е.
![]()
где t – время полета кузнечика. Значит, 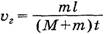 . Из рассмотрения движения кузнечика по вертикали получаем уравнение
. Из рассмотрения движения кузнечика по вертикали получаем уравнение ![]() . Откуда находим 2υв= g·t. Когда начальная скорость υ0 минимальна, то минимален и квадрат скорости. Используя неравенство Коши, мы может записать, что
. Откуда находим 2υв= g·t. Когда начальная скорость υ0 минимальна, то минимален и квадрат скорости. Используя неравенство Коши, мы может записать, что
![]() .
.
Удвоенное произведение скоростей легко получить:
![]()
Таким образом, минимальная начальная скорость кузнечика достигается при υв= υг и равна ![]() . Кузнечик должен подпрыгнуть под углом 45° к поверхности стола.
. Кузнечик должен подпрыгнуть под углом 45° к поверхности стола.
Решив данную задачу, мы фактически установили, какую минимальную кинетическую энергию должен сообщить кузнечик своему телу, чтобы попасть на другой конец соломинки.
Резонно задаться вопросом: является ли такой прыжок и энергетически наиболее экономичным для кузнечика?
Ответить на данный вопрос не так уж трудно. Энергия, затраченная кузнечиком во время отталкивания от соломинки, преобразуется в кинетические энергии его тела и соломинки. Значит,
![]()
![]() .
.
Здесь использовались ранее полученные уравнения:
![]()
После упрощения
![]()
Не забываем о неравенстве Коши:
![]()
![]()
Минимум энергии, который необходимо затратить кузнечику, чтобы перепрыгнуть на другой конец соломинки, равен
![]()
Этот минимум достигается при
![]() .
.
Из последнего уравнения легко получить, что кузнечик должен иметь
![]() ,
,
а значит,
![]() .
.
Видно, что υв> υг, а кузнечику следует подпрыгнуть под углом α, ![]() . Таким образом, энергетически более выгодно кузнечику придать своему телу большую кинетическую энергию и подпрыгнуть под углом, превышающим 45°. Лишь в случае m » М кузнечику следует иметь равные вертикальную и горизонтальную составляющие начальной скорости. Результат получился такой же, как и для стрельбы из пушки на наибольшую дальность, если учитывать сопротивление воздуха.
. Таким образом, энергетически более выгодно кузнечику придать своему телу большую кинетическую энергию и подпрыгнуть под углом, превышающим 45°. Лишь в случае m » М кузнечику следует иметь равные вертикальную и горизонтальную составляющие начальной скорости. Результат получился такой же, как и для стрельбы из пушки на наибольшую дальность, если учитывать сопротивление воздуха.
Задача 6. Какой должен быть наклон крыши, чтобы дождевая вода стекала с нее как можно быстрее? Трением пренебречь, считать начальную скорость осаждающихся капель равной нулю.
Решение. Рассмотрим движение отдельной капельки дождевой воды по крыше. Силы, действующие на нее, показаны на рисунке. Пусть капля осела на высоте h, пройти ей надо до края ската расстояние l, а по горизонтали b.
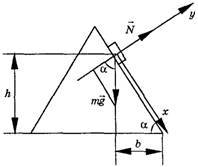
l, h и b связаны теоремой Пифагора l2 =h2 + b2.
Запишем динамическое уравнение движения капли в векторном виде: ![]() . Перейдем к скалярам:
. Перейдем к скалярам:
![]()
где 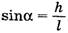 . Из первого уравнения системы находим
. Из первого уравнения системы находим 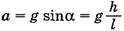 . С учетом того, что начальная скорость капли равна нулю, получим
. С учетом того, что начальная скорость капли равна нулю, получим
![]()
![]()
![]() .
.
А теперь опять вспомним о неравенстве Коши:
![]() .
.
Минимальное время стекания капли, равное 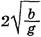 , достигается при
, достигается при 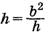 , то есть при h = b, что приводит к равнобедренному прямоугольному треугольнику, а значит, наклон крыши должен быть равен 45°.
, то есть при h = b, что приводит к равнобедренному прямоугольному треугольнику, а значит, наклон крыши должен быть равен 45°.
Задача 7. Небольшое тело соскальзывает с горки высотой H по склону, заканчивающемуся горизонтальным трамплином. Какова должна быть высота трамплина h, чтобы дальность полета тела при прочих равных условиях была наибольшей? Трение и сопротивление воздуха не учитывать.
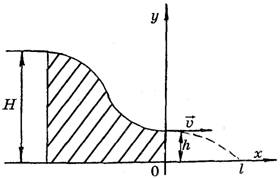
Решение. Определим скорость тела на горизонтальном участке трамплина на основе закона сохранения энергии 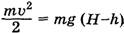 , откуда
, откуда 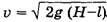 . Так как сопротивление воздуха не учитывается, то движение тела во время свободного падения по горизонтали описывается формулой x = υ·t, а по вертикали
. Так как сопротивление воздуха не учитывается, то движение тела во время свободного падения по горизонтали описывается формулой x = υ·t, а по вертикали 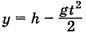 . В точке падения у = 0, время падения
. В точке падения у = 0, время падения 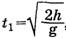 , дальность полета
, дальность полета 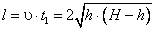 . Под знаком корня стоит произведение двух неотрицательных величин, а значит,
. Под знаком корня стоит произведение двух неотрицательных величин, а значит,
![]() .
.
Видно, что максимальная дальность полета тела равна высоте горки и достигается при h = H – h, откуда находим 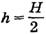 .
.
Задача 8. Тонкая положительная линза имеет фокусное расстояние F и дает действительное изображение предмета. Каково минимальное расстояние между предметом и его изображением?
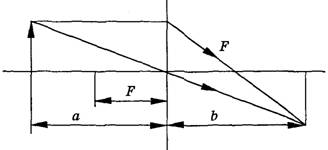
Решение. Запишем формулу для тонкой собирающей линзы
![]() (1)
(1)
Очевидно, что расстояние между предметом и его изображением l = a + b. Подставим b = l – a в (1).
![]() ,
, ![]() .
.
Преобразуем полученное выражение
![]()
![]() .
.
l принимает минимальное значение, когда минимальна сумма 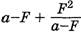 . Применим неравенство Коши
. Применим неравенство Коши
![]() .
.
Таким образом, получили lmin= 2F + 2F = 4F. Минимум достигается при ![]() , т.е. при a = 2F. Следует обратить внимание, что при этом изображение находится на таком же расстоянии от линзы, что и предмет.
, т.е. при a = 2F. Следует обратить внимание, что при этом изображение находится на таком же расстоянии от линзы, что и предмет.
Задача 9. Один моль идеального газа переводят из состояния 1 в состояние 2. Определите максимальную температуру, которую имел газ.
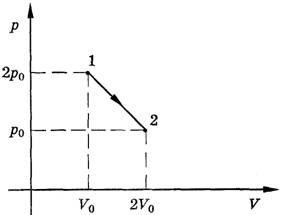
Решение. Обратим внимание, что переход 1-2 описывается линейной функцией p = –k·V + b. Коэффициенты k и b можно определить из системы уравнений:
![]()
Из первого уравнения вычтем второе: р0 = k·V0, ![]() . Подставим найденное k в первое уравнение:
. Подставим найденное k в первое уравнение:
![]() , b = 3р0.
, b = 3р0.
Итак, переход 1-2 описывается функцией 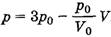 .
.
Уравнение состояния идеального газа p·V = ν·R·T. Подставим сюда найденное нами p(V).
![]() .
.
Температура становится максимальной, когда
![]()
![]()
принимает наибольшее значение.
Так как в нашем случае объем изменяется от V0 до 2V0, то V > 0 и 3V0 – V > 0, а значит, если V·(3V0 – V) достигает максимального значения, то и 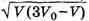 тоже становится максимальным. Но
тоже становится максимальным. Но
![]()
при V = 3V0 – V, т.е. при V = 1,5V0. Значит, V·(3V0 – V) = 2,25V02, откуда
![]() и
и ![]() .
.
| Выложил | alsak |
| Опубликовано | 25.09.08 |
| Просмотров | 16175 |
| Рубрика | Решение задач |
| Тема | Без тем |