Асламазов Л.Г. Силы трения и движение // Квант
Асламазов Л. Силы трения и движение // Квант. — 1980. — № 11. — С. 38-41.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Движению тела обычно препятствуют силы трения. Если соприкасаются поверхности твердых тел, их относительному движению мешают силы сухого трения. Характерной особенностью сухого трения является существование зоны застоя. Тело нельзя сдвинуть с места, пока абсолютная величина внешней силы не превысит определенного значения. До этого момента между поверхностями соприкасающихся тел действует сила трения покоя, которая уравновешивает внешнюю силу и растет вместе с ней (рис. 1).
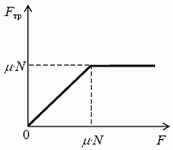
Рис. 1.
Максимальное значение силы трения покоя определяется формулой
![]()
где μ— коэффициент трения, зависящий от свойств соприкасающихся поверхностен; N — сила нормального давления.
Когда абсолютная величина внешней силы превышает значение Fтр max, возникает относительное движение — проскальзывание. Сила трения скольжения обычно слабо зависит от скорости относительного движения, и при малых скоростях ее можно считать равной Fтр max.
Движению тела в жидкости и газе препятствуют силы жидкого трения. Главное отличие жидкого трения от сухого — отсутствие зоны застоя. В жидкости или газе не возникают силы трения покоя, и поэтому даже малая внешняя сила способна вызвать движение тела. Сила жидкого трения при малых скоростях пропорциональна скорости, а при больших — квадрату скорости движения.
Задача 1. При экстренной остановке поезда, двигающегося со скоростью υ = 70 км/ч. тормозной путь составил s = 100 м. Чему равен коэффициент трения между колесами поезда и рельсами? Каким станет тормозной путь, если откажут тормоза в одном из n = 10 вагонов? Массу локомотива принять равной массе вагона; силами сопротивления воздуха пренебречь.
При торможении ускорение а поезду сообщает сила трения Fтр:
![]()
где Μ — масса всего состава. Сила трения 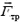 представляет собой равнодействующую всех сил трения, действующих на состав (рис. 2), и равна по модулю
представляет собой равнодействующую всех сил трения, действующих на состав (рис. 2), и равна по модулю 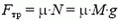 .
.

Рис. 2.
Следовательно,
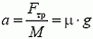 и
и ![]() .
.
С другой стороны, 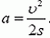 . Подставляя это значение в выражение для μ, получаем
. Подставляя это значение в выражение для μ, получаем
![]()
В том случае, когда не работают тормоза у одного из вагонов, суммарная сила трения, действующая на вагоны и локомотив, равна
![]()
где m — масса одного вагона. Масса всего состава равна Μ = (п + 1)∙m, так что ![]() . Ускорение поезда в этом случае равно
. Ускорение поезда в этом случае равно
![]()
а тормозной путь равен
![]()
***
Важно понимать, что сила трения не всегда тормозит движение. Во многих случаях движение становится возможным именно благодаря ей.
Смогли бы вы разбежаться на скользком льду? Очевидно, нет; и лучшем случае вам удалось бы бежать на месте. Сила трения между подошвами и землей, препятствуя проскальзыванию, создает необходимое для разгона ускорение.
Задача 2. При каком коэффициенте трения человек сможет вбежать на горку высотой h = 10 м с углом наклона α = 0,1 рад за время t = 10 с без предварительного разгона? Считать, что мощность человека не ограничивает время движения, а сопротивление воздуха мало.
Сила трения, действующая на человека, препятствует проскальзыванию и поэтому направлена вверх (рис. 3).
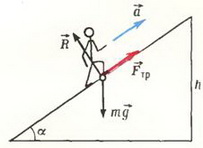
Рис. 3.
На человека также действуют сила притяжения к Земле m∙g и сила реакции R. Величина последней силы определяется из условия равенства нулю суммы проекций всех сил на направление, перпендикулярное плоскости горки (в этом направлении нет ускорения):
![]()
Как видно, сила реакции 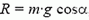 , а значит и равная ей по модулю сила нормального давления N, меньше силы тяжести.
, а значит и равная ей по модулю сила нормального давления N, меньше силы тяжести.
Напишем теперь второй закон Ньютона, спроектировав все силы на направление вдоль плоскости горки:
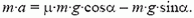
С другой стороны, ускорение связано со временем движения и пройденным путем кинематической формулой
![]()
Из последних двух уравнений для коэффициента трения получаем
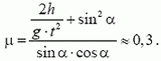
***
Если человек не вбегает на горку, а сбегает с нее, то сила трения, препятствуя скольжению, может тормозить его движение. Именно благодаря силе трения человеку удается медленно спускаться с горки.
Задача 3. Какую минимальную скорость будет иметь человек, сбежавший с горки высотой h = 10 м с наклоном α = 0.1 рад при коэффициенте трения μ = 0,05?
Проектируя силы, действующие па человека, на направление плоскости горки (рис. 4), для модуля ускорения получаем
![]()
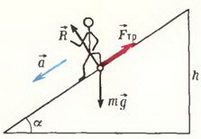
Рис. 4.
Конечная скорость человека
![]()
При 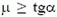 человек может стоять на горке и, следовательно, может спускаться с нее как угодно медленно.
человек может стоять на горке и, следовательно, может спускаться с нее как угодно медленно.
Разумеется, все сказанное относится не только к человеку, но и к автомашине. Сила трения между шинами и шоссе, препятствуя проскальзыванию, разгоняет автомобиль, когда колеса соединены с двигателем. Эта же сила, также препятствуя проскальзыванию, тормозит движение автомобиля, когда к колесам прижаты тормозные колодки.
***
Рассмотрим теперь роль силы трения при движении по окружности.
Задача 4. У края диска радиусом R лежит монета (рис. 5). Диск раскручивается так, что его угловая скорость линейно растет со временем: 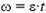 . В какой момент времени монета слетит с диска, если коэффициент трения между диском и монетой μ? Какой угол с направлением к центру диска образует сила трения в этот момент?
. В какой момент времени монета слетит с диска, если коэффициент трения между диском и монетой μ? Какой угол с направлением к центру диска образует сила трения в этот момент?
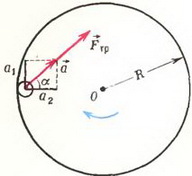
Рис. 5.
До тех пор пока монета лежит на диске, ее линейная скорость υ равна линейной скорости диска:
![]()
Как видно, эта скорость не постоянна, а линейно растет со временем. Следовательно, монета движется с ускорением, проекция которого на направление касательной к окружности равна 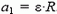 . Кроме того, поскольку монета движется по окружности, у нес есть и центростремительное ускорение (то есть проекция ускорения на направление к центру окружности)
. Кроме того, поскольку монета движется по окружности, у нес есть и центростремительное ускорение (то есть проекция ускорения на направление к центру окружности) 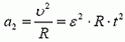 . Таким образом, ускорение монеты равно по модулю (см. рис. 5)
. Таким образом, ускорение монеты равно по модулю (см. рис. 5)
![]()
Единственной силой, действующей на монету в плоскости диска, является сила трения Fтр. По второму закону Ньютона она и создает ускорение а:
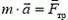 и
и 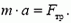
Подставляя в последнюю формулу выражения для а и для максимального значения силы трения 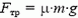 , получаем, что монета может лежать на плоскости до момента
, получаем, что монета может лежать на плоскости до момента
![]()
При ![]() монета слетит сразу же, так как сила трения будет не в состоянии обеспечить столь большое ускорение монеты.
монета слетит сразу же, так как сила трения будет не в состоянии обеспечить столь большое ускорение монеты.
Направление силы трения совпадает с направлением ускорения, поэтому
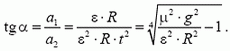
***
Многие задачи на силы трения удобно решать, применяя закон сохранения энергии.
Задача 5. Тело, скользящее со скоростью υ по гладкой поверхности, влетает на шероховатую поверхность с коэффициентом трения μ (рис. 6). При какой минимальной длине тела l оно остановится так, что часть его еще будет находиться на гладкой поверхности?
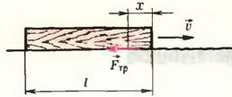
Рис. 6.
Из закона сохранения энергии следует, что начальная кинетическая энергия тела равна работе, совершаемой против сил трения:
![]()
При нахождении работы необходимо учесть, что сила трения меняется по мере перемещения тела с гладкой поверхности на шероховатую. Если на шероховатой поверхности находится часть тела длиной x,
![]()
то есть сила трения пропорциональна пройденному пути. Поэтому при перемещении всего тела работа
![]()
Подставляя это выражение в уравнение, выражающее закон сохранения энергии, для минимальной длины тела получаем
![]()
***
В заключение рассмотрим довольно часто встречающееся явление — заклинивание: в некоторых случаях невозможно преодолеть силу трения, даже прикладывая очень большую внешнюю силу.
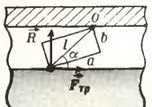
Задача 6. Стержень вытаскивают из трубы, имеющей диаметр, несколько больший диаметра стержня (рис. 7, а). В зазор между стержнем и трубой попадает песчинка, имеющая форму параллелепипеда (отношение ![]() ). Оцените, при каком значении коэффициента трения между песчинкой и поверхностями стержня и трубы стержень не удастся вытащить из трубы. Считать, что коэффициент трения между трубой и стержнем пренебрежимо мал.
). Оцените, при каком значении коэффициента трения между песчинкой и поверхностями стержня и трубы стержень не удастся вытащить из трубы. Считать, что коэффициент трения между трубой и стержнем пренебрежимо мал.

а
б
Рис. 7.
При движении стержня между ним и песчинкой возникает сила трения Fтр. Эта сила, действуя на песчинку, создает момент, вращающий ее вокруг точки О (рис. 7, б). Если этот момент больше момента силы реакции R, вращающего песчинку в обратную сторону, вытащить стержень не удастся, так как песчинка будет вдавливаться в стержень. Другими словами, если
![]()
стержень заклинит.
Подставляя в это неравенство выражение для максимальной силы трения Fтр = μ∙N, и учитывая, что сила реакции равна по модулю силе нормального давления: R = N, получаем, что при 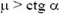 стержень вытащить не удастся. В нашем случае
стержень вытащить не удастся. В нашем случае 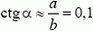 , так что при μ > 0,1 силу трения не удастся преодолеть даже очень большой внешней силой.
, так что при μ > 0,1 силу трения не удастся преодолеть даже очень большой внешней силой.
Упражнения
1. На наклонной плоскости лежит тело массой m. Найдите модуль Fтр силы трения, действующей на тело, в зависимости от угла наклона α и постройте соответствующий график. Коэффициент трения между телом и плоскостью μ.
2. Человек идет по скользкому льду. Оцените, какого максимального размера L шаги он может делать, чтобы не упасть. Длина ноги человека l = 1м, коэффициент трения о лед μ = 0,05.
3. На листе бумаги лежит монета массой m. С каким максимальным ускорением можно тянуть лист бумаги, чтобы монета с него не соскользнула, если коэффициент трения монеты о бумагу μ? Как при этом направлена сила трения, действующая на монету?
4. Нажимая на педаль «газ», водитель увеличивает мощность, развиваемую двигателем автомобиля. При какой мощности начнется пробуксовка колес автомобиля, если коэффициент трения между шинами и дорогой μ = 0,2, масса автомобиля m = 1000 кг, скорость υ = 60 км/ч, КПД двигателя η = 40%?
5. Водитель автомобиля внезапно усидел перед собой стену, преграждающую дорогу. Что выгоднее ему делать: затормозить или, свернуть в сторону?
6. На наклонной плоскости лежит брусок. Как он будет двигаться, если ему сообщить горизонтальный импульс, параллельный ребру наклонной плоскости?
Ответы
1. При 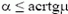 сила трения
сила трения ![]() , при
, при 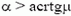 сила трения
сила трения 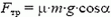
2. 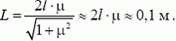
3. a = μ∙g, сила направлена в сторону, что и ускорение.
4. 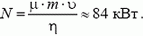
5. Выгоднее затормозить.
6. Брусок будет соскальзывать вниз.
| Выложил | alsak |
| Опубликовано | 05.02.09 |
| Просмотров | 21312 |
| Рубрика | Решение задач |
| Тема | Динамика |