Баканина Л.П. О силах трения // Квант
Баканина Л.П. О силах трения // Квант. — 1978. — № 11. — С. 48-51.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Многие школьники, поступающие в вузы, часто испытывают затруднения при решении задач, в которых действуют силы трения.
Вспомним об основных особенностях сил так называемого сухого трения — трения между двумя твердыми телами. Эти силы возникают всегда при непосредственном соприкосновении тел, направлены вдоль поверхности соприкосновения и действуют на каждое из соприкасающихся тел, причем действуют так, чтобы препятствовать движению одного тела относительно другого — если это силы трения скольжения, или так, чтобы препятствовать самому возникновению этого движения — если речь идет о силах трения покоя.
Абсолютная величина силы трения скольжения Fтp зависит от вида трущихся поверхностей и силы N нормального давления одного тела на другое:
Fтр = μ∙N,
где μ— коэффициент трения.
Сила трения покоя Fтp п всегда уравновешивает все остальные силы, действующие на тело вдоль поверхности соприкосновения. Ее абсолютная величина может принимать любые значения от нуля до некоторого максимального значения Fтp п max, которое обычно считают равным Fтpск:
0 ≤ Fтp п ≤ Fтp ск.
При решении задач прежде всего необходимо разобраться, с какими именно силами трения — покоя или скольжения — мы имеем дело. Рассмотрим несколько конкретных задач.
Задача 1. Ни горизонтальном столе лежат два бруска массой Μ1 =7 кг и М2 = 10 кг, связанные нитью. Еще одна нить, привязанная к бруску массой Μ1, переброшена через блок, укрепленный на краю стола, и к ней подвешен груз массой m = 1 кг (рис. 1). Коэффициент трения между брусками и столом μ = 0,1. Определите натяжения обеих нитей и силы трения, действующие на каждый из брусков.
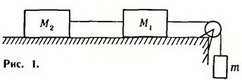
Во-первых, выясним, будут двигаться бруски или нет. Они могут начать двигаться под действием силы натяжения Т1 правой нити, а она, по абсолютной величине, не может превысить силу тяжести груза массой m:
T1 ≤ m∙g = 10 Н.
Максимальное значение силы трения покоя для обоих брусков
Fтp п max = μ∙(M1 + M2)∙g = 17 Н.
Так как Т1 < Fтp п max, бруски покоятся. Очевидно, что покоится и груз массой m; следовательно,
T1 = m∙g = 10 Н.
Теперь рассмотрим но отдельности бруски массой M1 и М2. На правый брусок действуют силы натяжения нитей T1 и T2 и сила трения Fтp1 (рис. 2) (нас интересуют только те силы, которые лают горизонтальные проекции, отличные от нуля).
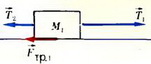
Рис. 2.
Максимальное значение силы трения
Fтp1 max = μ∙M1∙g = 7 Н < Т1 = 10 Н,
значит, одна только сила трения не может уравновесить брусок. Как только она достигнет своего наибольшего значения, натянется вторая нить — появится сила натяжения Т2.
Первый брусок будет покоиться, если
T1 = Fтр1 + Т2,
где
Fтр1 = Fтр1 max = 7 Н.
Отсюда
Т2 = T1 – Fтр1 max = 3 Н.
На второй брусок действуют две силы: сила натяжения нити Т2 и сила трения Fтр2 (рис. 3). Поскольку
Fтp2 max = μ∙M2∙g = 10 Н > Т2 = 3 Н,
сила трения Fтp2 может уравновесить силу Т2:
Fтp2 = Т2 = 3 Н.
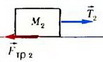
Рис. 3.
Задача 2. Брусок лежит на доске. Доску приподнимают за один край. Как зависит абсолютная величина силы трения, действующей на брусок, от угла наклона доски α (рис. 4)? Коэффициент трения между бруском и доской μ, масса бруска m.
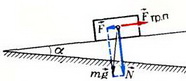
Рис. 4.
При достаточно малых углах наклона брусок покоится на доске. При этом сила трения покоя Fтр п уравновешивает силу F — составляющую силы тяжести бруска, направленную вдоль наклонной плоскости:
Fтр п = F = m∙g∙sin α.
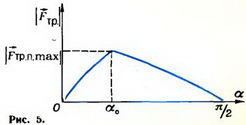
С увеличением угла α сила трения покоя растет, и при некотором угле α0 она достигает своего максимального значения:
Fтp п max = Fтpск = μ∙N или m∙g∙sin α0 = μ∙m∙g∙cos α0.
Отсюда
tg α0 = μ и ![]() .
.
При дальнейшем увеличении угла α тело скользит по доске, и сила трения является силой трения скольжения:
Fтpск = μ∙N = μ∙m∙g∙cos α.
График зависимости абсолютной величины силы трения от утла наклона доски α показан на рисунке 5: до угла α0 сила трения возрастает по закону синуса, а дальше она убывает по закону косинуса.
Задача 3. Прямоугольный брусок, размеры которого показаны на рисунке 6, тянут равномерно по горизонтальной плоскости за веревку, угол наклона которой α можно менять. Коэффициент трения бруска о плоскость равен μ. При какой величине угла α0 брусок начнет приподниматься?
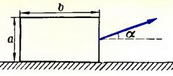
Рис. 6.
Рассмотрим все силы, которые действуют на брусок. Это сила натяжения веревки Т, сила тяжести m∙g, сила реакции опоры N (равная по абсолютной величине силе нормального давления) и сила трения скольжения Fтр ск (так как брусок движется). При угле наклона α0, когда брусок начнет приподниматься, силы N и Fтр ск проходят через точку А (рис. 7).
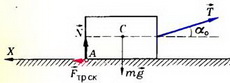
Рис. 7.
Так как брусок движется равномерно и прямолинейно, сумма действующих на него сил и сумма моментов этих сил относительно любой оси должны быть равны нулю. Следовательно, равны нулю сумма проекций всех сил на ось X:
Fтр ск – T∙cos α0 = 0
и сумма моментов сил относительно центра тяжести С:
![]()
Из этих двух уравнении с учетом того, что Fтр ск = μ∙N, получаем
![]()
Задача 4. Ребенок скатывается с горки на санках. Высота горки Η = 15 м, угол наклона к горизонту α = 30º, а коэффициент трения линейно нарастает вдоль пути от μ1 = 0 у вершины горы до μ2 = 0,4 у подножия. Какую скорость будут иметь санки у подножия горы?
Так как абсолютная величина силы трения скольжения при движении санок изменяется, а значит, движение санок не будет равноускоренным, задачу проще и удобнее решать с помощью закона сохранения энергии:
![]()
Здесь m·g·H — потенциальная энергия санок на вершине горы, 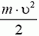 — их кинетическая энергия у подножия и A — работа против силы трения скольжения Fтp ск..
— их кинетическая энергия у подножия и A — работа против силы трения скольжения Fтp ск..
Для определения A нарисуем график зависимости Fтp ск. от пути s (рис. 8). У вершины горы
Fтp ск.1 = μ1·m·g·cos α = 0,
у подножия
Fтp ск.2 = μ2·m·g·cosα,
весь путь
![]()
Работа А численно равна площади заштрихованного треугольника на рисунке 8:
![]()
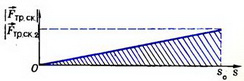
Рис. 8.
Тогда из закона сохранения энергии получаем:
![]()
Упражнения
1. Брусок массой m, размеры которого показаны на рисунке 9, стоит на наклонной плоскости с углом наклона α. На брусок начинает действовать сила F, параллельная наклонной плоскости. При каком абсолютном значении этой силы брусок опрокинется? Известно, что соскальзывать с наклонной плоскости брусок при этом не будет.
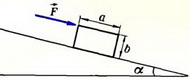
Рис. 9.
2. Какую работу нужно затратить, чтобы втащить сани с грузом (общей массой m = 30 кг) на горку высотой H = 10 м? Угол наклона горки к горизонту α = 30°, а коэффициент трения между санями и горкой линейно убывает вдоль пути от μ1 = 0,5 у подножия до μ2 = 0,1 у вершины.
3. Мешок с мукой сползает без начальной скорости с высоты Н = 2 м по доске, наклоненной под углом α2 = 45° к горизонту. После спуска мешок попадает на горизонтальную поверхность. Коэффициент трения мешка о доску и горизонтальную поверхность μ = 0,5. На каком расстоянии от конца доски мешок остановится?
Ответы
1. 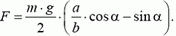
2. ![]()
3. ![]()
| Выложил | alsak |
| Опубликовано | 05.02.09 |
| Просмотров | 22499 |
| Рубрика | Решение задач |
| Тема | Динамика |