Баканина Л.П. Силы трения // Квант
Баканина Л.П. Силы трения // Квант. — 1973. — № 9. — С. 68-71.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Сила трения часто вызывает у поступающих в вуз серьезные затруднения, особенно сила трения покоя. Чему равна ее величина? Как она направлена? Попытаемся ответить на эти вопросы, разобрав несколько конкретных примеров. Задачи, рассмотренные в статье, в разные годы предлагались на вступительных экзаменах в Московский физико-технический институт, и многие абитуриенты не смогли с ними справиться.
Прежде всего вспомним некоторые особенности сил сухого трения, возникающего между двумя твердыми телами. При непосредственном взаимодействии (соприкосновении) этих тел возникают силы, действующие на каждое из них. Согласно третьему закону Ньютона эти силы равны по величине и противоположны по направлению. Составляющие этих сил, направленные перпендикулярно соприкасающимся поверхностям, называют силами нормального давления. Составляющие, направленные вдоль поверхности, называют силами трения.
Пусть тело лежит на горизонтальном столе. Будем действовать на него горизонтальной силой, величина которой постепенно увеличивается. До тех пор, пока эта сила меньше определенной величины Fmax, тело будет сохранять состояние покоя потому, что на тело со стороны стола действует сила трения покоя, по величине равная приложенной силе. Направление силы трения противоположно возможному перемещению. Если бы не было трения, тело сразу начало бы скользить. Можно сказать, что тело «пытается» начать скользить, но трение удерживает его на месте. Если же величина воздействия больше Fmax, возникает скольжение. Сила трения скольжения, как известно, не зависит от величины сил, действующих на тело вдоль поверхности:
Fск = μ∙N.
Величина силы нормального давления N не зависит ни от величины касательных взаимодействий, ни от свойств трущихся поверхностей.
Опыт показывает, что обычно Fск несколько меньше Fmax. Однако отличие это невелико, и при решении почти всех задач считают, что Fск = Fmax. Это приближение стало настолько привычным, что его обычно даже и не оговаривают. Точно так же пренебрегают зависимостью силы трения от скорости. На рисунке 1 пунктиром изображена (несколько преувеличено) зависимость силы трения от скорости, наблюдаемая на опыте, а сплошной линией — обычное упрощенное представление этой зависимости.

Рис. 1.
Перейдем теперь к разбору конкретных задач, при решении которых особенности сил трения играют существенную роль.
Задача 1. Поезд, подходя к станции со скоростью υ = 72 км/ч, начинает равномерно тормозить. Каково наименьшее время торможения поезда до полной остановки, безопасное для спящих пассажиров? Коэффициент трения пассажира о полку μ = 0,2.
При торможении поезда скорость движения полки, на которой лежит пассажир, уменьшается, и если бы пассажир сохранил прежнюю скорость, он начал бы скользить по полке вперед, по ходу движения поезда. Однако, как только он начинает или, вернее, как только он «пытается» начать скользить, возникает сила трения. Она сообщает пассажиру тормозящее ускорение. Если это ускорение равно ускорению поезда, скорость пассажира все время равна скорости полки, на которой он лежит, и пассажир не скользит по полке. Максимальное возможное ускорение может сообщить максимальная сила трения покоя, которая, как мы уже говорили, приближенно равна Fcк = μ·N. Согласно второму закону Ньютона
m·amax= μ·N,
где m — масса спящего пассажира, а N — сила его нормального давления на полку. Для горизонтальной полки N = m·g и amax = μ·g. Значит, ускорение поезда, при котором пассажиры не падают с полок, a ≤ μ·g.
Время торможения до полной остановки
![]()
Задача 2. Автомобиль, трогаясь с места, равномерно набирает скорость, двигаясь по горизонтальному участку дороги, представляющему собой дугу окружности в 30° радиуса R = 100 м. С какой максимальной скоростью автомобиль может выехать на прямой участок пути? Коэффициент трения колес о землю μ = 0,3.
Единственная внешняя горизонтальная сила, действующая на автомобиль, — это сила трения. Разгон, как мы предполагаем, происходит без проскальзывания, следовательно, мы имеем дело с силой трения покоя. Только эта сила и может сообщить автомобилю необходимое ускорение.
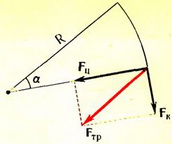
Рис. 2.
Так как движение автомобиля по окружности — это движение с ускорением, сила трения должна быть направлена под углом к скорости (рис.2). При этом составляющая Fk, направленная вдоль скорости, сообщает автомобилю необходимое для разгона ускорение, а составляющая Fn, направленная по радиусу окружности, изменяет направление скорости так, чтобы автомобиль двигался по окружности. Центростремительное ускорение 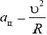 , следовательно,
, следовательно, 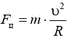 . Скорость максимальна в конце разгона, значит, тогда же максимальна и Fц. Так как по условию задачи автомобиль набирает скорость равномерно, сила Fк постоянна.
. Скорость максимальна в конце разгона, значит, тогда же максимальна и Fц. Так как по условию задачи автомобиль набирает скорость равномерно, сила Fк постоянна.
Как известно, пройденный путь, ускорение и скорость в конце пути связаны соотношением 2aц∙s = υ2. Отсюда 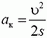 , а сила
, а сила 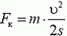 .
.
Геометрическая сумма сил Fк и Fц не должна превышать максимальной силы трения покоя Fтр = μ∙m∙g. Так как эти силы перпендикулярны друг другу, то в конце разгона
![]()
Отсюда
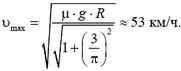
Задача 3. Небольшой кубик массы m покоится на шероховатой плоскости, наклоненной к горизонту под углом α. Коэффициент трения μ = 2·tg α. Определить, с какой минимальной горизонтальной силой F, лежащей в плоскости склона (рис. 3), нужно толкать, кубик, чтобы он начал двигаться.
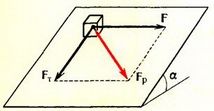
Рис. 3.
При μ > tg α под действием только силы тяжести кубик не будет скользить по наклонной плоскости, так как направленная вдоль наклонной плоскости проекция силы тяжести Fт = m∙g∙sin α меньше максимальной силы трения покоя Fтр = μ∙m∙g∙cos α. Если приложить горизонтальную силу F, то результирующая сила, действующая вдоль наклонной плоскости, будет равна (см. рис. 3).
![]()
Если Fp ≥ Fтр, кубик начнет скользить, так как сила трения покоя уже не может его уравновесить. Минимальное значение необходимой для этого силы F можно найти из условия
F2 + (m∙g∙sin α)2 = (μ∙m∙g∙cos α)2.
Отсюда
![]()
Задача 4. Хоккейная шайба падает на лед под углом α к вертикали со скоростью υ0. С какой скоростью шайба начнет скользить по льду, если после удара о лед она не подпрыгивает? Коэффициент трения шайбы о лед равен μ.
Изменение количества движения, согласно второму закону Ньютона, равно импульсу действующей силы. По условию задачи вертикальная составляющая вектора количества движения за время удара обращается в нуль. Значит, импульс силы нормального давления на поверхность N·Δt равен
N·Δt = m·υ0·cos α,
где Δt — время удара, а N — средняя сила давления шайбы на лед во время удара.
Так как по условию задачи шайба после удара скользит, сила трения во время удара — это сила трения скольжения Fск = μ·N. Время соударения Δt очень мало, а m·Δυверт — конечная величина, поэтому сила нормального давления при ударе гораздо больше веса шайбы. Среднее значение силы трения во время удара
![]()
Импульс силы трения за время удара
Fтр·Δt = μ·N·Δt = μ·m·υ0·cos α.
Изменение горизонтальной составляющей количества движения шайбы за время удара равно
m·υ – m·υ0·sin α = –μ·m·υ0·cos α,
откуда υ = υ0·sin α – μ·υ0·cos α.
Если коэффициент трения μ очень мал, изменение горизонтальной составляющей количества движения шайбы тоже мало, и приближенно можно считать, что для горизонтальной проекции выполняется закон сохранения количества движения.
Следует отметить, что приведенное решение справедливо только тогда, когда μ ≤ tg α. Попробуйте разобраться самостоятельно, что будет происходить в случае, если μ > tg α.
Упражнения
1. Тело опускают без начальной скорости на ленту транспортера, движущуюся со скоростью υ = 3,6 км/ч. Коэффициент трения между телом и лентой μ = 1. Какой путь пройдет тело по ленте?
2. Изучая дорожное происшествие, автоинспектор установил, что след торможения автомобиля, ехавшего по асфальтовой дороге, равен 60 м. С какой скоростью ехал автомобиль, если коэффициент трения колес об асфальт при торможении равен 0,5?
3. Маховик радиуса R = 0,2 м насажен на закрепленную горизонтальную ось радиуса r = 0,02 м. Сила трения между маховиком и осью Fск = 103 Н. Для того чтобы легче было снять маховик с оси, к его ободу прикладывается сила F = 80 Н, создающая вращающий момент относительно оси (рис. 4). С какой минимальной силой N нужно тянуть маховик вдоль оси, чтобы снять его?
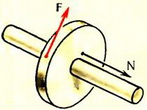
Рис. 4.
4. Две дороги, АВ и CD, направленные под углом 120° друг к другу, выходят на круглую асфальтированную площадь радиуса r = 68 м (рис. 5). С какой максимальной постоянной скоростью может ехать по площади автомобиль, чтобы попасть с одной дороги на другую, если коэффициент трения между асфальтом и шинами автомобиля μ = 0,4?
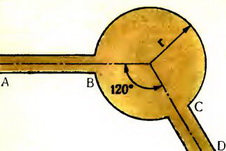
Рис. 5.
Ответы
1. 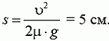
2. υ = 87 км/ч.
3. N = 600 Н.
4. 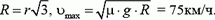
| Выложил | alsak |
| Опубликовано | 12.02.09 |
| Просмотров | 16839 |
| Рубрика | Решение задач |
| Тема | Динамика |