Плис В. О динамике криволинейного движения // Квант
Плис В. О динамике криволинейного движения // Квант. —·2005. — №2. — С. 30-31, 34-35.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Из школьного курса физики известно, что равномерное движение по окружности — так называют движение материальной точки по окружности с постоянной по величине скоростью — есть движение с ускорением.
Это ускорение обусловлено равномерным изменением с течением времени направления скорости точки. В любой момент времени вектор ускорения направлен к центру окружности, а его величина постоянна и равна
![]()
где υ — линейная скорость точки, R — радиус окружности, ω — угловая скорость радиуса-вектора точки, T — период обращения. В этом случае ускорение называют центростремительным, или нормальным, или радиальным.
Очевидно, что возможно криволинейное движение не только по окружности и не обязательно равномерное. Поговорим немного о кинематике произвольного криволинейного движения. Тем более что в прошлом году в программу вступительных экзаменов по физике, например в МГУ им. М.В.Ломоносова, включили вопрос об ускорении материальной точки при произвольном движении по криволинейной траектории.
Рассмотрим сначала неравномерное движение материальной точки по окружности. При таком движении изменяется со временем не только направление вектора скорости 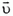 , но и его величина. В этом случае приращение
, но и его величина. В этом случае приращение 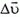 вектора скорости за малое время от t до t + Δt удобно представить в виде суммы:
вектора скорости за малое время от t до t + Δt удобно представить в виде суммы: 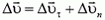 (рис. 1). Здесь
(рис. 1). Здесь 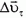 — касательная тангенциальная составляющая приращения скорости, сонаправленная с вектором скорости и обусловленная приращением величины вектора скорости на
— касательная тангенциальная составляющая приращения скорости, сонаправленная с вектором скорости и обусловленная приращением величины вектора скорости на 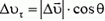 , а
, а 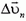 — нормальная составляющая, обусловленная (как и в случае равномерного движения по окружности) вращением вектора скорости. Тогда естественно и ускорение представить в виде суммы касательной (тангенциальной) и нормальной составляющих:
— нормальная составляющая, обусловленная (как и в случае равномерного движения по окружности) вращением вектора скорости. Тогда естественно и ускорение представить в виде суммы касательной (тангенциальной) и нормальной составляющих:
![]()
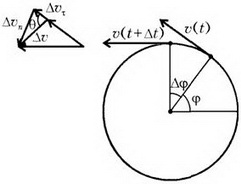
Рис. 1
Для проекций вектора ускорения на касательное и нормальное направления справедливы соотношения
![]()
Отметим, что касательная составляющая aτ ускорения характеризует быстроту изменения величины скорости, а нормальная составляющая аnхарактеризует быстроту изменения направления скорости. По теореме Пифагора,
![]()
В случае движения по произвольной криволинейной траектории все указанные соотношения также справедливы, при этом в формуле для нормального ускорения аn под величиной R надо понимать радиус такой окружности, с элементарной дужкой которой совпадает участок криволинейной траектории в малой окрестности того места, где находится движущаяся материальная точка. Величину R называют радиусом кривизны траектории в данной точке.
Теперь рассмотрим несколько конкретных задач на криволинейное движение, предлагавшихся в последние годы на вступительных экзаменах и олимпиадах по физике в ведущих вузах страны.
Задача 1. Камень брошен со скоростью υ0 под углом α к горизонту. Найдите радиус R кривизны траектории в окрестности точки старта. Ускорение свободного падения g известно.
Для ответа на вопрос задачи воспользуемся соотношением для нормального ускорения: 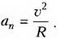
В малой окрестности точки старта υ = υ0(рис. 2). Нормальное ускорение аn есть проекция ускорения свободного падения g на нормаль к траектории: аn= g·cos α. Это дает 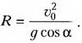
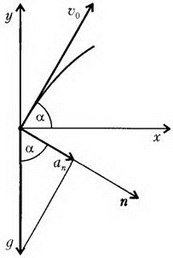
Рис. 2
Задача 2. Определите вес P тела массой m на географической широте φ. Ускорение, сообщаемое силой тяжести, равно g. Землю считайте однородным шаром радиусом R.
Напомним, что вес тела 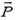 — это сила, обусловленная тяготением, с которой тело действует на опору или подвес. Допустим, что тело лежит на поверхности вращающейся Земли. На него действуют сила тяжести
— это сила, обусловленная тяготением, с которой тело действует на опору или подвес. Допустим, что тело лежит на поверхности вращающейся Земли. На него действуют сила тяжести 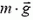 , направленная к центру Земли, и сила реакции опоры
, направленная к центру Земли, и сила реакции опоры 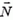 (рис.3). По третьему закону Ньютона,
(рис.3). По третьему закону Ньютона, 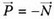 . Поэтому для определения веса тела найдем силу реакции
. Поэтому для определения веса тела найдем силу реакции 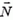 .
.
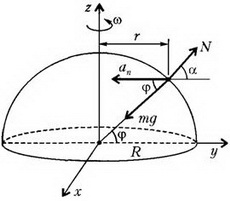
Рис. 3
В инерциальной системе отсчета, центр которой находится в центре Земли, тело равномерно движется по окружности радиусом r = R·cos φ с периодом одни сутки, т.е. T= 86400 с, и циклической частотой
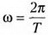 = 7,3·10–5 с–1.
= 7,3·10–5 с–1.
Ускорение тела по величине равно
аn = ω2·r = ω2·R·cos φ
и направлено к оси вращения Земли. Из этого следует, что равнодействующая сил тяжести и реакции опоры тоже должна быть направлена к оси вращения Земли. Тогда при 0 < φ< π/2 сила реакции образует с перпендикуляром к оси вращения некоторый угол α ≠ φ. По второму закону Ньютона,
![]()
Перейдем к проекциям сил и ускорения на радиальное направление:
![]()
и на направление, перпендикулярное плоскости, в которой происходит движение:
![]()
Исключая α из двух последних соотношений, находим вес тела, покоящегося на вращающейся Земле:
![]()
Задача 3. Расстояние от Земли до двойной звезды в созвездии Центавра равно L = 2,62·105 а.е. Наблюдаемое угловое расстояние между звездами периодически изменяется с периодом T = 80 лет и достигает наибольшего значения φ = 0,85·10–5 рад. Определите суммарную массу М звезд. Постоянная всемирного тяготения G = 6,67·10–11 (Н·м2/кг2), 1 а.е = 1,5·1011 м. Орбиты звезд считайте круговыми.
Под действием гравитационных сил
![]()
звезды движутся равномерно с периодом Tпо окружностям радиусов r1и r2 вокруг центра масс системы со скоростями υ1 и υ2соответственно (рис. 4).
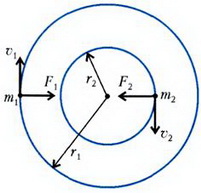
Рис. 4
По второму закону Ньютона,
![]()
![]()
Сложив эти равенства (после сокращения на m1 и m2 соответственно), получим
![]()
Отсюда с учетом соотношений
![]()
приходим к ответу
![]() = 3,5 1027 кг.
= 3,5 1027 кг.
Задача 4. На горизонтальной платформе стоит сосуд с водой (рис. 5). В сосуде закреплен тонкий стержень АВ, наклоненный к горизонту под углом α. Однородный шарик радиусом R может скользить без трения вдоль стержня, проходящего через его центр. Плотность материала шарика ρ0, плотность воды ρ, ρ0 < ρ. При вращении системы с постоянной угловой скоростью вокруг вертикальной оси, проходящей через нижний конец А стержня, центр шарика устанавливается на расстоянии L от этого конца. С какой по величине силой F шарик действует на стержень? Какова угловая скорость ω вращения платформы? При какой минимальной угловой скорости ωmin шарик «утонет», т.е. окажется у дна сосуда?
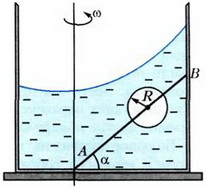
Рис. 5
Обозначим объем шарика V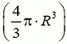 . На шарик будут действовать три силы: сила тяжести ρ0·V·g, сила нормальной реакции N со стороны стержня (шарик действует на стержень с такой же по величине и противоположной по направлению силой) и сила Архимеда FA. Найдем архимедову силу.
. На шарик будут действовать три силы: сила тяжести ρ0·V·g, сила нормальной реакции N со стороны стержня (шарик действует на стержень с такой же по величине и противоположной по направлению силой) и сила Архимеда FA. Найдем архимедову силу.
Рассмотрим движение жидкости в отсутствие шарика. Любой элементарный объем воды равномерно движется по окружности радиусом r в горизонтальной плоскости. Следовательно, вертикальная составляющая суммы сил давления (силы Архимеда) уравновешивает силу тяжести, действующую на жидкость в рассматриваемом объеме, а горизонтальная составляющая сообщает этой жидкости центростремительное ускорение аn = ω2·r. При замещении жидкости шариком эти составляющие не изменяются, а сила, действующая на водяной шарик со стороны тонкого стержня, равна нулю. Тогда вертикальная составляющая силы Архимеда по величине равна силе тяжести водяного шара:
FAz = ρ·V·g,
а направленная к оси вращения составляющая силы Архимеда сообщает водяному шару центростремительное ускорение аn = ω2·L·cos α и по величине равна
FAn = ρ·V·ω2·L·cos α.
Под действием приложенных сил шарик движется равномерно по окружности радиусом L·cos α в горизонтальной плоскости (рис. 6).
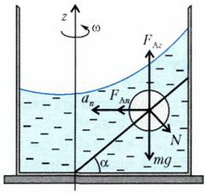
Рис. 6
По второму закону Ньютона,
![]()
Переходя к проекциям сил и ускорений на вертикальную ось, находим
ρ·V·g – ρ0·V·g – N·cos α = 0.
Проектируя силы и ускорения в горизонтальной плоскости на радиальное направление, получаем
ρ0·V·ω2·L·cos α = ρ·V·ω2·L·cos α – N·sin α.
Из двух последних соотношений определяем величину силы нормальной реакции стержня, а значит, и силу давления шарика на стержень:
![]()
и угловую скорость:
![]()
Как видим, с ростом угловой скорости ω расстояние L уменьшается. В момент, когда шар приблизится ко дну, 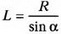 , при этом
, при этом
![]()
Задача 5. Однородную цепочку длиной L поместили на гладкую сферическую поверхность радиусом R так, что один ее конец закреплен на вершине сферы. Верхний конец цепочки освобождают. С каким по величине ускорением at будет двигаться сразу после освобождения каждый элемент цепочки? Масса единицы длины цепочки ρ. Ускорение свободного падения g.
Рассмотрим элементарный участок цепочки длиной ΔL = R·Δφ (рис. 7). Его масса равна Δm = ρ·ΔL. Силы, действующие на выделенный участок, показаны на рисунке. По второму закону Ньютона,
![]()
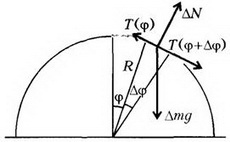
Рис. 7
Переходя к проекциям сил и ускорений на касательное направление, получаем
![]()
Перепишем полученное соотношение в виде
![]()
Просуммируем приращения силы натяжения по всей длине цепочки:
![]()
Теперь учтем, что на свободных концах цепочки силы натяжения обращаются в ноль, т.е. 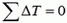 , что ускорение aτ одинаково у всех элементарных фрагментов,
, что ускорение aτ одинаково у всех элементарных фрагментов, 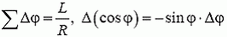 , и получим
, и получим
![]()
Задача 6. Ведущие колеса паровоза соединены реечной передачей, одно звено которой представляет собой плоскую горизонтальную штангу, шарнирно прикрепленную к спицам соседних колес на расстоянии R/2 от оси, где R — радиус колеса. При осмотре паровоза механик поставил на эту штангу ящик и по рассеянности забыл его там. Паровоз трогается с места и очень медленно набирает скорость. Оцените скорость υ1 паровоза, при которой ящик начнет проскальзывать относительно штанги. Коэффициент трения скольжения ящика по штанге μ = 0,4, радиус колеса R = 0,8 м, ускорение свободного падения g = 10 м/с2.
Перейдем в систему отсчета, связанную с паровозом (рис. 8). Поскольку разгон происходит очень медленно, эту систему можно считать инерциальной.
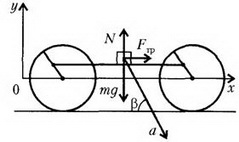
Рис. 8
До начала проскальзывания ящик движется по окружности радиусом r = R/2. По второму закону Ньютона,
![]()
Вектор ускорения ящика направлен к центру окружности и по величине равен а = ω2·r,где ω — угловая скорость вращения колес паровоза. Обозначим угол, который вектор ускорения образует в данный момент времени с горизонтом, буквой β. Переходя к проекциям сил и ускорения на горизонтальную и вертикальную оси, с учетом того, что Fтр ≤ μ·N, получаем
![]()
![]()
Исключив отсюда силу реакции опоры, приходим к неравенству
![]()
Наибольшее значение выражения
![]()
где угол α таков, что 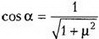 и
и 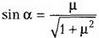 ,достигается при β = α и равно
,достигается при β = α и равно 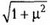 . Движение груза будет происходить без проскальзывания до тех пор, пока угловая скорость вращения колес паровоза будет удовлетворять неравенству
. Движение груза будет происходить без проскальзывания до тех пор, пока угловая скорость вращения колес паровоза будет удовлетворять неравенству
![]()
Отсюда для искомой скорости паровоза υ1получаем
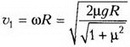 = 2,4 м/с.
= 2,4 м/с.
Задача 7. Гладкий желоб состоит из горизонтальной части АВ и дуги окружности BD радиусом R = 5 м (рис. 9). Шайба скользит по горизонтальной части со скоростью υ0 = 10 м/с . Определите величину ускорения шайбы в точке С и угол β, который вектор 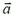 ускорения шайбы в этот момент составляет с нитью. Радиус ОС образует с вертикалью угол α = 60°. Ускорение свободного падения g =10 м/с2.
ускорения шайбы в этот момент составляет с нитью. Радиус ОС образует с вертикалью угол α = 60°. Ускорение свободного падения g =10 м/с2.
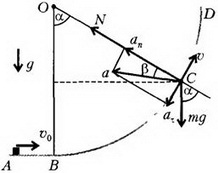
Рис. 9
Для нахождения ускорения шайбы в точке С найдем тангенциальную aτи нормальную an величины составляющих ускорения в этой точке.
На тело, движущееся в вертикальной плоскости по дуге BD,в любой точке действуют силы тяжести m·g и реакции опоры N. По второму закону Ньютона,
![]()
Перейдем к проекциям сил и ускорения на тангенциальное направление:
m·aτ= –m·g·sin α, откуда aτ= –g·sin α ≈ –8,7 м/с2.
Для определения нормальной составляющей ускорения найдем величину υскорости шайбы в точке С (поскольку 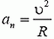 ). Обратимся к энергетическим соображениям. Потенциальную энергию шайбы на горизонтальной части желоба будем считать равной нулю. Тогда, по закону сохранения полной механической энергии,
). Обратимся к энергетическим соображениям. Потенциальную энергию шайбы на горизонтальной части желоба будем считать равной нулю. Тогда, по закону сохранения полной механической энергии,
![]()
откуда
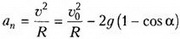 = 10 м/с2.
= 10 м/с2.
Величину ускорения шайбы в точке С найдем по теореме Пифагора:
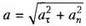 ≈ 13,2 м/с2.
≈ 13,2 м/с2.
В точке С вектор ускорения 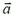 образует с нитью угол β такой, что
образует с нитью угол β такой, что
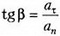 ≈ 0,87, откуда β ≈ 41°.
≈ 0,87, откуда β ≈ 41°.
Задача 8. По гладкой проволочной винтовой линии радиусом R с шагом h, ось которой вертикальна, скользит с нулевой начальной скоростью бусинка массой m. За какое время T бусинка опустится по вертикали на Н? С какой по величине F силой бусинка действует на проволоку в этот момент? Ускорение свободного падения g.
На бусинку действуют силы тяжести 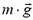 и нормальной реакции
и нормальной реакции 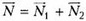 , где
, где 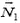 направлена горизонтально (перпендикулярно плоскости рисунка 10), а
направлена горизонтально (перпендикулярно плоскости рисунка 10), а 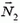 лежит в одной плоскости с векторами
лежит в одной плоскости с векторами 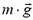 и
и 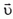 .
.
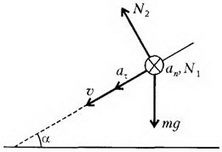
Рис. 10
Для ответа на вопросы задачи найдем касательную и нормальную составляющие ускорения. По второму закону Ньютона,
![]()
Переходя к проекциям сил и ускорения на касательное направление, находим aτ= g·sin α. Здесь α — угол наклона вектора скорости к горизонту такой, что
![]()
По закону сохранения энергии,
![]() и
и 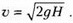
Касательная составляющая ускорения постоянна, начальная скорость равна нулю, следовательно, модуль вектора скорости растет со временем по линейному закону. Отсюда для искомого времени получаем
![]()
Для определения нормальной составляющей ускорения перейдем в подвижную систему отсчета, поступательно движущуюся относительно лаборатории по вертикали вниз со скоростью υ·sin α. В этой системе бусинка ускоренно движется по окружности радиусом R со скоростью υ·cos α, при этом нормальная составляющая ускорения бусинки по величине равна 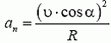 . Так как ускорение подвижной системы сонаправлено с
. Так как ускорение подвижной системы сонаправлено с 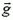 , нормальная составляющая ускорения бусинки при переходе в лабораторную систему отсчета не изменится (это следует из правила сложения ускорений).
, нормальная составляющая ускорения бусинки при переходе в лабораторную систему отсчета не изменится (это следует из правила сложения ускорений).
Из второго закона Ньютона находим составляющие силы, с которой проволока действует на бусинку:
![]()
где 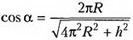 .
.
По третьему закону Ньютона бусинка действует на проволоку силой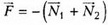 , величина (модуль) которой равна
, величина (модуль) которой равна
![]()
Упражнения
1. Сферический воздушный шар радиусом R = 5 м удерживается вертикальной веревкой, его центр находится на высоте H = 6 м над горизонтальной поверхностью. С этой поверхности бросают камень так, что он перелетает шар, почти касаясь его в верхней точке. С какой минимальной скоростью υ0следует бросать камень и на каком расстоянии s от центра шара будет находиться в этом случае точка бросания?
Указание: ускорение свободного падения у поверхности Земли в этой и последующих задачах равно g = 10 м/с2.
2. Известно, что спутник, находящийся на орбите, высота которой h = 3,6104 км, обращается вокруг Земли за одни сутки и может «висеть» над одной и той же точкой экватора. Допустим, что обсуждается вопрос о запуске на такую же высоту спутника, который будет «висеть» над Санкт-Петербургом. Какую по величине и направлению силу тяги F должен развивать двигатель спутника, чтобы удерживать его на заданной орбите? Масса спутника m = 103 кг, Санкт-Петербург находится на широте φ = 60°, радиус Земли R = 6,4 103 км.
3. По гладкому столу движутся два тела с массами m1и m2,соединенные легкой нерастяжимой нитью длиной L.В некоторый момент первое тело останавливается, а скорость второго равна υи перпендикулярна нити. Найдите силу Tнатяжения нити.
4. Однородную цепочку массой m и длиной L поместили на гладкую сферическую поверхность радиусом R = 4L так, что один ее конец закреплен на вершине сферы. Верхний конец цепочки освобождают. Найдите наибольшую величину Tmах силы натяжения цепочки сразу после ее освобождения. Указание: для рассматриваемых в задаче углов считайте sin α ≈ α, cos α ≈ 1 – α2/2.
5. В задаче 6 из текста статьи найдите скорость υ2, при которой ящик начнет подпрыгивать.
6. Для экономии места въезд на один из высочайших в Японии мостов устроен в виде винтовой линии, обвивающей цилиндр радиусом R. При движении по такой дороге вектор скорости автомобиля составляет угол α с горизонтальной плоскостью. Найдите направление и величину суммы сил, действующих на автомобиль массой m, движущийся по такой дороге с постоянной по величине скоростью υ. Ось винтовой линии вертикальна.
Ответы
1. 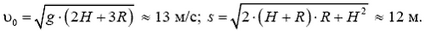
2. Сила тяги равна ![]() и перпендикулярна плоскости движения спутника.
и перпендикулярна плоскости движения спутника.
3. 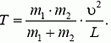
4. 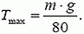
5. 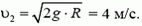
6. Сумма сил равна 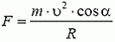 и направлена по горизонтали к оси винтовой линии.
и направлена по горизонтали к оси винтовой линии.
| Выложил | alsak |
| Опубликовано | 24.02.09 |
| Просмотров | 24511 |
| Рубрика | Решение задач |
| Тема | Динамика |