Можаев В. Центр масс механической системы // Квант
Можаев В. Центр масс механической системы // Квант. — 2006. — №2. — С. 25-28.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Рассмотрим произвольную механическую систему твердых тел с заданным взаимным расположением в пространстве и с известными массами. Поступательное движение такой системы под действием внешних сил эквивалентно движению материальной точки, имеющей массу, равную массе системы, и находящейся под воздействием результирующей силы всех внешних сил.
Геометрическую точку, в которой располагается эта материальная точка, называют центром инерции или центром масс данной системы. Для произвольной неподвижной прямоугольной системы координат (ее называют также лабораторной системой) координаты центра масс определяются следующими формулами:
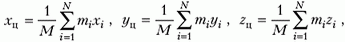
где mi, xi, yi, zi – массы и координаты центров масс тел, входящих в систему, а M – суммарная масса всех тел.
Если сумма внешних сил, действующих на систему, равна нулю, то центр масс остается неподвижным или движется прямолинейно с некоторой постоянной скоростью (в зависимости от предыстории). В этом случае удобно рассматривать движение тел под действием внутренних сил в инерциальной системе отсчета, связанной с центром масс. В такой системе отсчета импульс системы равен нулю и будет оставаться нулевым при любых взаимодействиях между телами системы.
Перейдем к разбору конкретных задач.
Задача 1. Определите, какую часть своей кинетической энергии теряет частица массой m1 при упругом лобовом столкновении с неподвижной частицей массой m2.
Пусть скорость налетающей частицы массой m1 равна υ1, тогда скорость движения центра масс системы будет равна
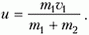
Перейдем в систему отсчета, связанную с центром масс нашей системы. В этой системе скорость частицы массой m1 равна
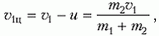
а скорость частицы массой m2 составляет
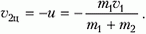
За положительное направление выбрано направление скорости первой частицы. Получается, чтов системе центра масс мы имеем уже другую ситуацию: обе частицы движутся навстречу друг другу с равными по величине импульсами
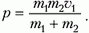
Когда частицы встретятся, возможны три варианта:
1) частицы не провзаимодействуют и пролетят, сохраняя свои скорости и импульсы;
2) произойдет нецентральный упругий удар, при котором частицы разлетятся, также сохраняя свои скорости и импульсы, но уже лежащие на прямой, проходящей по одному из диаметров сферы с центром в точке столкновения;
3) произойдет центральный упругий удар, при котором скорости и импульсы частиц также остаются неизменными по величине, но меняют свои направления на противоположные.
Найдем скорости наших частиц после центрального удара, но уже снова в неподвижной системе координат, где скорость частицы массой m1 до удара была υ1. После удара первая частица будет двигаться со скоростью
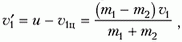
а вторая со скоростью
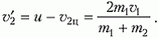
До удара кинетическая энергия налетающей частицы в неподвижной системе координат была
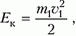
а после удара стала
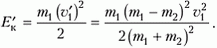
Потеря кинетической энергии равна
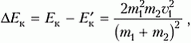
что составляет от начальной энергии долю
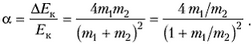
Зависимость α от отношения m1/m2 изображена на рисунке 1. При m1 = m2 α = 1 т.е. происходит полная потеря энергии. При уменьшении отношения m1/m2 α уменьшается и при 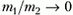 доля теряемой энергии также стремится к нулю. Вот почему, например, в ядерных реакторах для замедления нейтронов используется рассеяние их на ядрах легких атомов – дейтерия, углерода. Для дейтерия, ядро которого состоит из протона и нейтрона, m1/m2 = 0,5 и α = 0,89. В случае же ядра атома углерода m1/m2 = 1/12 и α = 0,28.
доля теряемой энергии также стремится к нулю. Вот почему, например, в ядерных реакторах для замедления нейтронов используется рассеяние их на ядрах легких атомов – дейтерия, углерода. Для дейтерия, ядро которого состоит из протона и нейтрона, m1/m2 = 0,5 и α = 0,89. В случае же ядра атома углерода m1/m2 = 1/12 и α = 0,28.
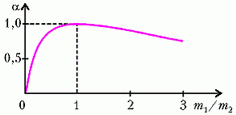
Рис. 1
Задача 2. Две частицы, массы которых m1 и m2 (m1 > m2), движутся навстречу друг другу вдоль одной прямой с одинаковыми скоростями. После упругого столкновения тяжелая частица отклоняется от направления своего первоначального движения на угол α = 30° в лабораторной системе отсчета или на угол β = 60° в системе центра масс. Определите отношение m1/m2.
Обозначим начальные скорости частиц в лабораторной системе координат через υ0. Тогда скорость движения центра масс нашей системы частиц будет
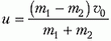
– здесь за положительное направление выбрано направление скорости частицы массой m1.
Перейдем в систему координат, связанную с центром масс. В этой системе скорость частицы массой m1 до столкновения равна
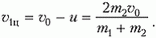
Аналогичная скорость частицы массой m2 составляет
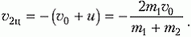
Импульсы частиц в этой системе координат равны по величине:
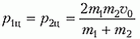
и направлены в противоположные стороны как до соударения, так и после него. Но после соударения импульсы частиц лежат на прямой, которая составляет угол β с направлением первоначального движения.
На рисунке 2 изображена векторная диаграмма импульсов для частицы массой m1.
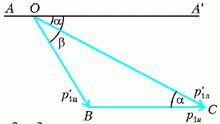
Рис. 2
На этой диаграмме прямая АА´ соответствует направлению первоначального движения частиц. Отрезок ОВ равен импульсу частицы массой m1 в системе центра масс после столкновения, отрезок ОС равен импульсу этой же частицы после соударения, но уже в лабораторной системе отсчета. А вот отрезок ВС – это импульс, который добавляется при переходе из системы центра масс в лабораторную систему, величина этого импульса равна
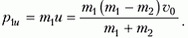
При заданных значениях углов α и β треугольник ОВС оказывается равнобедренным, поскольку угол BOC = β – α = 30º, a угол BCO = α = 30º (BC || AA´). Из этого следует, что ОВ = ВС, или
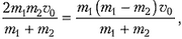
откуда получаем 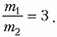
Задача 3. На прямолинейную горизонтальную спицу насажены два шарика, которые могут скользить по ней без трения (рис. 3). К шарику массой m прикреплена легкая пружина жесткостью k. Эта система неподвижна, а шарик массой 2m движется со скоростью υ0. Определите скорость шарика массой 2m после отрыва от пружины и время контакта этого шарика с пружиной. Радиусы шаров много меньше длины пружины.
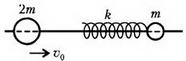
Рис. 3
Скорость центра масс в лабораторной системе координат составляет
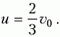
Перейдем в систему отсчета, связанную с центром масс. Скорость шарика массой 2m до взаимодействия с пружиной в этой системе равна
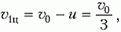
а скорость шарика массой m направлена в противоположную сторону и равна по величине
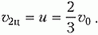
Как только шарик массой 2m достигнет пружины, скорости шариков начнут уменьшаться, а пружина будет сжиматься. В некоторый момент, когда вся кинетическая энергия шариков перейдет в потенциальную энергию упругой деформации пружины, шарики остановятся, а затем начнут ускоряться в противоположных направлениях. Когда пружина примет свою первоначальную длину, шарик массой 2m оторвется от пружины и будет иметь скорость, равную υ1ц и направленную в другую сторону по отношению к первоначальной. Но это – скорость в системе центра масс, а нам нужно найти скорость этого шарика в лабораторной системе отсчета.
Для этого перейдем обратно в лабораторную систему отсчета. В этой системе скорость шарика массой 2m, очевидно, будет равна
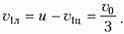
Относительная потеря кинетической энергии шарика составит
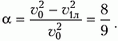
Для проверки воспользуемся результатом, полученным в задаче 1:
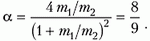
Это совпадение закономерно, поскольку данная задача является частным случаем задачи 1 при m1/m2 = 2.
Для ответа на второй вопрос заметим, что когда шарик массой 2m находится в контакте с пружиной, эта ситуация эквивалентна колебаниям шарика на горизонтально расположенной пружине, один конец которой закреплен. Закрепленным концом является центр масс, который остается неподвижным в системе отсчета, связанной с центром масс. Если длина нашей пружины l, то длина эквивалентной пружины составляет
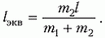
Теперь нужно сообразить, чему будет равна жесткость пружины длиной lэкв, если жесткость исходной пружины k. Это право мы предоставляем читателю, а сами напишем готовый результат:
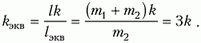
Очевидно, что время контакта шарика массой 2m с пружиной равно половине периода гармонических колебаний шарика на эквивалентной пружине:
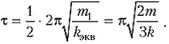
Задача 4. Клин массой 2m с углом наклона к горизонту α (cos α = 2/3) находится на гладкой горизонтальной поверхности стола (рис. 4). Через блок, укрепленный на вершине клина, перекинута легкая нить, связывающая грузы массами m и 3m. Груз массой 3m может скользить вдоль вертикальной направляющей AB, закрепленной на клине. Этот груз вначале удерживают неподвижно на расстоянии Н = 27 см от стола, а затем отпускают. На какое расстояние сместится клин к моменту касания груза массой 3m стола? Массами блока и направляющей AB пренебречь.
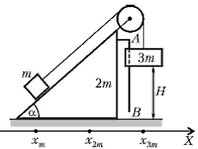
Рис. 4
После того как отпустили груз массой 3m, на нашу систему тел в горизонтальном направлении (ось X) никакие внешние силы не действуют, поэтому горизонтальная координата центра масс системы будет оставаться неизменной. Пусть в произвольный момент времени (после освобождения груза массой 3m) горизонтальные координаты центров масс трех тел будут такими: xm – координата груза массой m, х2m – координата клина, x3m – координата груза массой 3m (начало отсчета – произвольное). Тогда горизонтальная координата центра масс системы будет равна
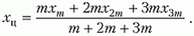
Поскольку величина xц остается постоянной, можно записать
xm + 2x2m + 3x3m = const.
За время падения груза массой 3m происходит изменение всех трех координат, причем эти изменения будут связаны между собой соотношением
Δxm + 2Δx2m + 3Δx3m = 0,
или, так как Δx2m = Δx3m,
Δxm + 5Δx2m = 0.
Опускание груза массой 3m на величину H приводит к перемещению груза массой m вдоль наклонной плоскости также на H, а вдоль оси X – на H·cos α. Но это – перемещение относительно клина, а полное горизонтальное перемещение груза массой m будет равно
Δxm = H·cos α + Δx2m.
Тогда, с учетом соотношения между Δxm и Δx2m, для перемещения клина получим
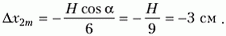
Знак «минус» означает, что клин сместится влево.
Задача 5. Определите минимальное значение кинетической энергии α-частицы, необходимое для осуществления реакции 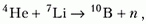 если реакция идет с поглощением энергии Q = 2,85 МэВ. Ядро лития неподвижно.
если реакция идет с поглощением энергии Q = 2,85 МэВ. Ядро лития неподвижно.
До реакции мы имеем α-частицу, или ядро атома гелия, и ядро лития, а после реакции образуются ядро бора и нейтрон. Если мы подсчитаем суммарные энергии покоя частиц до реакции и после реакции, то увидим, что энергия покоя ядра бора и нейтрона больше, чем энергия покоя α-частицы и ядра лития. Эта разность как раз и равна поглощаемой энергии Q при данной реакции. Такие ядерные реакции, проходящие с поглощением энергии, называют эндотермическими реакциями. Реакции, идущие, наоборот, с выделением энергии, называют экзотермическими. Отсюда понятно, что если исходные частицы неподвижны, то эндотермическая реакция не пойдет. Значит, налетающая на мишень частица должна обладать некоторой минимальной энергией, при которой начнется реакция. Величину этой энергии называют пороговой.
Наиболее удобно рассмотреть процесс неупругого взаимодействия частиц в системе отсчета, связанной с центром масс системы. Обозначим скорость α-частицы в лабораторной системе отсчета через υα. Тогда скорость движения центра масс равна
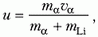
где mα и mLi – массы α-частицы и ядра лития. Скорость α-частицы в системе центра масс составляет здесь за положительное направление выбрано направление скорости α-частицы в лабораторной системе отсчета. Скорость ядра лития в системе центра масс равна
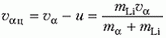
– здесь за положительное направление выбрано направление скорости α-частицы в лабораторной системе отсчета. Скорость ядра лития в системе центра масс равна
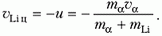
В этой системе отсчета при пороговой скорости α-частицы образовавшееся ядро бора и нейтрон должны покоиться. Запишем закон сохранения полной энергии до реакции и после реакции:
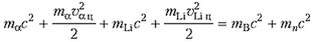
– энергии частиц здесь записаны для нерелятивистского случая. Подставляя в это уравнение выражения для υαц и учитывая, что
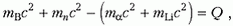
получим
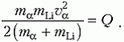
Отсюда находим минимальную кинетическую энергию α-частицы в лабораторной системе отсчета:
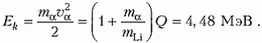
Упражнения
1. Вдоль прямолинейной горизонтальной спицы могут скользить без трения две муфты. Муфта массой m с прикрепленной к ней легкой пружиной жесткостью k движется со скоростью υ0, а муфта массой 4m покоится (рис. 5). Определите скорость муфты массой 4m после ее отрыва от пружины и время контакта этой муфты с пружиной. Размеры муфт много меньше длины пружины.
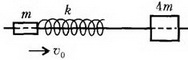
Рис. 5
2. На гладкой горизонтальной поверхности стола находится брусок в форме прямоугольного параллелепипеда, на котором укреплены ступенчатый блок с радиусами шкивов r и R (R = 4r) и вертикальная штанга ВС (рис. 6). На шкивы намотаны легкие нити, прикрепленные к грузам массами m и 5m. Груз массой m может скользить вдоль штанги ВС. Вначале груз массой 5m удерживают в покое, а затем отпускают. К моменту удара груза массой m о стол другой груз не достигает блока, а брусок за это время смещается на расстояние s = 2,5 см. На каком расстоянии от стола находился груз массой m вначале? Массами блока и штанги пренебречь.
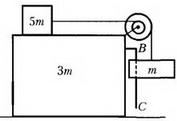
Рис. 6
3. Движущаяся частица претерпевает упругое столкновение с покоящейся частицей такой же массы. Докажите, что после столкновения, если оно не было лобовым, частицы разлетятся под прямым углом друг к другу.
4. Какова кинетическая энергия α-частицы, если при попадании в ядро азота 14N происходит реакция  сопровождающаяся поглощением энергии Q = 1 МэВ, а образовавшийся протон покоится в лабораторной системе отсчета?
сопровождающаяся поглощением энергии Q = 1 МэВ, а образовавшийся протон покоится в лабораторной системе отсчета?
Ответы
1. 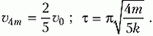
2. 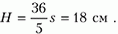
4. Ek = 1,3 МэВ.
| Выложил | alsak |
| Опубликовано | 02.03.09 |
| Просмотров | 25616 |
| Рубрика | Решение задач |
| Тема | Законы сохранения |