Черноуцан А.И. Задачи на центр масс // Квант
Черноуцан А. Задачи на центр масс // Квант. — 1996. — № 2. — С. 43-45.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
При решении механических задач неоценимую помощь может оказать использование понятия центра масс системы материальных точек. Одни задачи просто невозможно решить, не прибегая к этому понятию, решение других с его помощью может стать гораздо проще и нагляднее.
Перед тем как обсуждать конкретные задачи, напомним основные свойства центра масс и проиллюстрируем их примерами.
Центром масс (центром инерции) системы материальных точек назовем точку, характеризующую распределение масс в системе, координаты которой определяются формулами
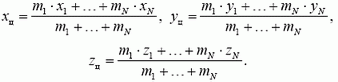
Здесь mi — массы материальных точек, образующих систему, xi, yi, zi — координаты этих точек. Читатели, знакомые с понятием радиуса-вектора, предпочтут векторную запись:
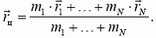 (1)
(1)
Пример 1. Найдем положение центра масс, простейшей системы, состоящей из двух точек, массы которых m1 и m2 и расстояние между ними l (рис. 1).
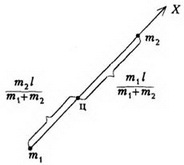
Рис. 1
Направив ось X от первой точки ко второй, получим, что расстояние от первой точки до центра масс (т.е. координата центра масс) равно 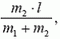 а расстояние от центра масс до второй точки равно
а расстояние от центра масс до второй точки равно 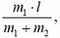 т.е. отношение расстояний обратно отношению масс. Значит, в этом случае положение центра масс совпадает с центром тяжести.
т.е. отношение расстояний обратно отношению масс. Значит, в этом случае положение центра масс совпадает с центром тяжести.
Обсудим некоторые свойства центра масс, что, как нам кажется, наполнит физическим содержанием приведенное выше несколько формальное определение этого понятия.
1) Положение центра масс не изменится, если какую-то часть системы заменить одной точкой с массой, равной массе этой подсистемы, и находящейся в ее центре масс.
Пример 2. Рассмотрим плоский однородный треугольник и найдем положение его центра масс. Разделим треугольник на тонкие полоски, параллельные одной из сторон, и заменим каждую полоску точкой, расположенной в ее середине. Так как все такие точки лежат на медиане треугольника, центр масс тоже должен лежать на медиане. Повторяя рассуждения для каждой из сторон, получаем, что центр масс находится на пересечении медиан.
2) Скорость центра масс можно найти, взяв производную по времени от обеих частей равенства (1):
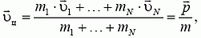 (2)
(2)
где 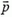 — импульс системы, m — полная масса системы. Видно, что скорость центра масс замкнутой системы постоянна. Значит, если связать с центром масс поступательно движущуюся систему отсчета, то она будет инерциальной.
— импульс системы, m — полная масса системы. Видно, что скорость центра масс замкнутой системы постоянна. Значит, если связать с центром масс поступательно движущуюся систему отсчета, то она будет инерциальной.
Пример 3. Поставим однородный стержень длиной l вертикально на гладкую плоскость (рис. 2) и отпустим. В процессе падения как горизонтальная составляющая его импульса, так и горизонтальная составляющая скорости центра масс будут оставаться равными нулю. Поэтому в момент падения центр стержня окажется в том месте, где первоначально стоял стержень, а концы стержня сместятся по горизонтали на 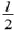 .
.
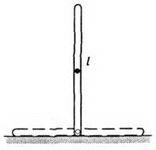
Рис. 2
3) Ускорение центра масс равно производной от его скорости по времени:
 (3)
(3)
где в правой части равенства стоят только внешние силы, так как все внутренние силы сокращаются по третьему закону Ньютона. Получаем, что центр масс, движется так, как двигалась бы воображаемая точка с массой, равной массе системы, под действием результирующей внешней силы. Наверное, это самое физическое свойство центра масс.
Пример 4. Если бросить палку, приведя ее при этом во вращение, то центр масс палки (ее середина) будет двигаться с постоянным ускорением 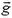 по параболе (рис. 3).
по параболе (рис. 3).
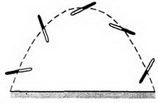
Рис. 3
4) Пусть система точек находится в однородном поле тяжести. Тогда суммарный момент сил тяжести относительно любой оси, проходящей через центр масс, равен нулю. Это значит, что равнодействующая сил тяжести проходит через центр масс, т.е. центр масс является также центром тяжести.
5) Потенциальная энергия системы точек в однородном поле тяжести вычисляется по формуле
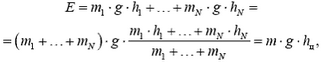
где hц — высота центра масс системы.
Пример 5. При выкапывании в однородном фунте ямы глубиной h и разбрасывании грунта по поверхности его потенциальная энергия возрастает на 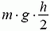 , где m — масса извлеченного грунта.
, где m — масса извлеченного грунта.
6) И еще одно полезное свойство центра масс. Кинетическая энергия системы точек может быть представлена в виде суммы двух слагаемых: кинетической энергии общего поступательного движения системы, равной 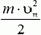 , и кинетической энергии Eотн движения относительно системы отсчета, связанной с центром масс:
, и кинетической энергии Eотн движения относительно системы отсчета, связанной с центром масс:
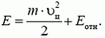
Пример 6. Кинетическая энергия обруча, катящегося без проскальзывания по горизонтальной поверхности со скоростью υ, равна
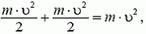
так как относительное движение в этом случае представляет собой чистое вращение, для которого линейная скорость точек обруча равна υ (полная скорость нижней точки должна быть равна нулю).
Теперь приступим к разбору задач на использование центра масс.
Задача 1. Однородный стержень лежит на гладкой горизонтальной поверхности. К стержню прикладывают две одинаковые по величине, но противоположные по направлению горизонтальные силы: одна сила приложена к середине стержня, другая — к его концу (рис. 4). Относительно какой точки начнет поворачиваться стержень?
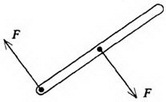
Рис. 4
На первый взгляд может показаться, что осью вращения будет точка, лежащая посередине между точками приложения сил. Однако уравнение (3) показывает, что поскольку сумма внешних сил равна нулю, то равно нулю и ускорение центра масс. Значит, центр стержня будет оставаться в покое, т.е. служить осью вращения.
Задача 2. Тонкий однородный стержень длиной l и массой m привели в движение вдоль гладкой горизонтальной поверхности так, что он движется поступательно и одновременно вращается с угловой скоростью ω. Найдите, натяжение стержня в зависимости от расстояния x до его центра.
Перейдем в инерциальную систему отсчета, связанную с центром стержня. Рассмотрим движение куска стержня, заключенного между рассматриваемой точкой стержня (расположенной на расстоянии x от центра) и его концом (рис. 5).
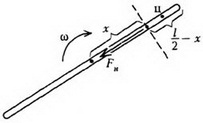
Рис. 5
Единственной внешней силой для этого куска является искомая сила натяжения Fн, масса равна 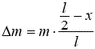 , а его центр масс движется по окружности радиусом
, а его центр масс движется по окружности радиусом 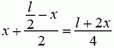 с ускорением
с ускорением 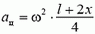 . Записывая уравнение движения центра масс выделенного куска, получим
. Записывая уравнение движения центра масс выделенного куска, получим
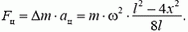
Задача 3. Двойная звезда состоит из двух звезд-компонентов массами m1 и m2, расстояние между которыми не меняется и остается равным L. Найдите период вращения двойной звезды.
Рассмотрим движение звезд-компонентов в инерциальной системе отсчета, связанной с центром масс двойной звезды. В этой системе отсчета звезды движутся с одной и той же угловой скоростью по окружностям разных радиусов (рис. 6).
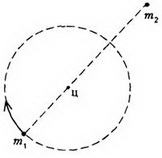
Рис. 6
Радиус вращения звезды массой m1 равен 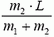 (см. Пример 1), а ее центростремительное ускорение создается силой притяжения к другой звезде:
(см. Пример 1), а ее центростремительное ускорение создается силой притяжения к другой звезде:
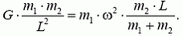
Видим, что период вращения двойной звезды равен
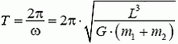
и определяется полной массой двойной звезды, независимо от того, как она распределена между звездами-компонентами.
Задача 4. Две точечные массы m и 2m связаны невесомой нитью длиной l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорость массы 2m равна нулю, а скорость массы m равна υ и направлена перпендикулярно нити (рис. 7). Найдите натяжение нити и период вращения системы.
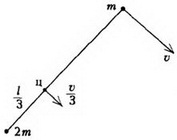
Рис. 7
Центр масс системы находится на расстоянии 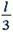 от массы 2m и движется со скоростью
от массы 2m и движется со скоростью 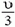 . В системе отсчета, связанной с центром масс, точка массой 2m движется по окружности радиусом
. В системе отсчета, связанной с центром масс, точка массой 2m движется по окружности радиусом 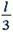 со скоростью
со скоростью 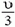 . Значит, период вращения равен
. Значит, период вращения равен 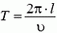 (проверьте, что такой же ответ получается, если рассмотреть точку массой m). Натяжение нити найдем из уравнения движения любой из двух точек:
(проверьте, что такой же ответ получается, если рассмотреть точку массой m). Натяжение нити найдем из уравнения движения любой из двух точек:
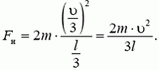
Задача 5. На гладкой горизонтальной плоскости лежат два одинаковых бруска массой m каждый, связанных легкой пружиной жесткостью k (рис. 8). Первому бруску сообщают скорость υ0 в направлении от второго бруска. Опишите движение системы. Через какое время деформация пружины впервые достигнет максимального значения?

Рис. 8
Центр масс системы будет перемещаться с постоянной скоростью 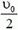 . В системе отсчета центра масс начальная скорость каждого бруска равна
. В системе отсчета центра масс начальная скорость каждого бруска равна 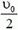 , а жесткость половинной пружины, которая соединяет его с неподвижным центром масс, составляет 2k (жесткость пружины обратно пропорциональна ее длине). Период таких колебаний равен
, а жесткость половинной пружины, которая соединяет его с неподвижным центром масс, составляет 2k (жесткость пружины обратно пропорциональна ее длине). Период таких колебаний равен
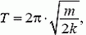
а амплитуда колебаний каждого бруска, которую можно найти из закона сохранения энергии, составляет
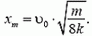
В первый раз деформация станет максимальной через четверть периода, т.е. через время 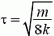 .
.
Задача 6. Шар массой m налетает со скоростью υ на покоящийся шар массой 2m. Найдите скорости обоих шаров после упругого центрального удара.
В системе отсчета, связанной с центром масс, полный импульс двух шаров равен нулю как до, так и после coyдарения. Легко догадаться, какой ответ для конечных скоростей удовлетворяет одновременно и этому условию, и закону сохранения энергии: скорости останутся такими же, как до удара, по величине, но изменят свои направления на противоположные. Скорость центра масс системы равна 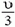 . В системе центра масс первый шар движется со скоростью
. В системе центра масс первый шар движется со скоростью 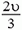 , а второй шар движется навстречу первому со скоростью
, а второй шар движется навстречу первому со скоростью 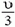 . После удара шары будут разлетаться с такими же скоростями. Осталось вернуться в первоначальную систему отсчета. Применяя закон сложения скоростей, находим, что конечная скорость шара массой m равна
. После удара шары будут разлетаться с такими же скоростями. Осталось вернуться в первоначальную систему отсчета. Применяя закон сложения скоростей, находим, что конечная скорость шара массой m равна 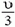 и направлена назад, а скорость покоившегося раньше шара массой 2m равна
и направлена назад, а скорость покоившегося раньше шара массой 2m равна 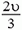 и направлена вперед.
и направлена вперед.
Отметим, что в системе центра масс очевидным является утверждение, что при ударе относительная скорость шаров не меняется по величине, но меняется по направлению. А так как разность скоростей при переходе в другую инерциальную систему отсчета не изменяется, можно считать, что мы вывели это важное соотношение и для первоначальной системы отсчета:
υ1 – υ2 = u1 – u2,
где буква υ используется для обозначения начальных скоростей, а u — для конечных. Это уравнение можно решать совместно с законом сохранения импульса вместо закона сохранения энергии (куда скорости входят во второй степени).
Задача 7. Известно, что при упругом нецентральном ударе двух одинаковых шаров, один из которых до удара покоился, угол разлета равен 90°. Докажите это утверждение.
В системе центра масс нецентральный удар можно описать следующим образом. До удара шары сближаются с одинаковыми импульсами, после удара они разлетаются с такими же по величине, но противоположно направленными импульсами, а прямая разлета поворачивается на некоторый угол относительно прямой сближения. Чтобы перейти обратно в начальную систему отсчета, надо каждую конечную скорость сложить (векторно!) со скоростью центра масс. В случае одинаковых шаров скорость центра масс равна 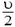 , где υ — скорость налетающего шара, и в системе отсчета центра масс шары сближаются и разлетаются с одинаковыми скоростями
, где υ — скорость налетающего шара, и в системе отсчета центра масс шары сближаются и разлетаются с одинаковыми скоростями 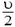 . В том, что после сложения каждой конечной скорости со скоростью центра масс получаются взаимно перпендикулярные векторы, можно убедиться из рисунка 9. А можно и просто проверить, что скалярное произведение векторов
. В том, что после сложения каждой конечной скорости со скоростью центра масс получаются взаимно перпендикулярные векторы, можно убедиться из рисунка 9. А можно и просто проверить, что скалярное произведение векторов 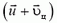 и
и 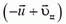 обращается в ноль в силу того, что модули векторов
обращается в ноль в силу того, что модули векторов 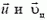 равны друг другу.
равны друг другу.
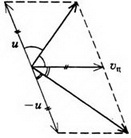
Рис. 9
Упражнения
1. Стержень массой m и длиной l шарнирно закреплен за один из концов. Стержень отклонили на некоторый угол от вертикального положения и отпустили. В момент прохождения вертикального положения скорость нижней точки равна υ. Найдите натяжение в средней точке стержня в этот момент времени.
2. Стержень массой m и длиной l вращают в горизонтальной плоскости с угловой скоростью ω вокруг одного из его концов. Найдите зависимость натяжения стержня от расстояния x до оси вращения, если на другом конце закреплен маленький грузик массой М.
3. Найдите период колебаний для системы, описанной в задаче 5 статьи, но для брусков различных масс m1 и m2.
4. Выведите известные общие формулы для упругого центрального удара двух шаров, используя переход в систему отсчета центра масс.
5. Шар массой m1 налетает на покоящийся шар меньшей массы m2. Найдите максимально возможный угол отклонения налетающего шара при упругом нецентральном ударе.
Ответы
1. 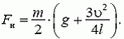
2. 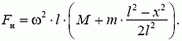
3. 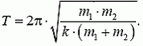
5. 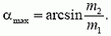
| Выложил | alsak |
| Опубликовано | 08.03.09 |
| Просмотров | 45783 |
| Рубрика | Решение задач |
| Тема | Законы сохранения |