Асламазов Л.Г. Закон сохранения импульса. Реактивная сила // Квант
Асламазов Л. Закон сохранения импульса. Реактивная сила // Квант. — 1979. — № 10. — С. 49-53.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Одна из возможных формулировок второго закона Ньютона утверждает, что изменение импульса (количества движения) механической системы равно импульсу внешних сил:
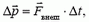 (1)
(1)
где 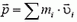 — полный импульс системы,
— полный импульс системы, 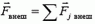 — векторная сумма внешних сил, действующих на систему.
— векторная сумма внешних сил, действующих на систему.
Для замкнутой (изолированной) системы 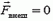 и, следовательно,
и, следовательно,
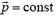 (2)
(2)
— суммарный импульс системы есть величина постоянная. Это — закон сохранения импульса. Он позволяет найти конечные скорости взаимодействующих тел, образующих изолированную систему, не вдаваясь в детали взаимодействия.
Следует помнить, что уравнение (2) — векторное, и ответ может существенно зависеть от направления начальных скоростей тел.
Задача 1. По гладкой горизонтальной поверхности движется тележка массой M со скоростью 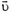 (рис. 1). В нее стреляют из ружья, причем пуля массой m, летящая со скоростью
(рис. 1). В нее стреляют из ружья, причем пуля массой m, летящая со скоростью 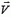 , застревает в тележке. Какой станет скорость тележки после попадания в нее пули в случае: а) когда скорость пули направлена горизонтально, так же как скорость тележки, б) когда скорость пули направлена вертикально вниз?
, застревает в тележке. Какой станет скорость тележки после попадания в нее пули в случае: а) когда скорость пули направлена горизонтально, так же как скорость тележки, б) когда скорость пули направлена вертикально вниз?
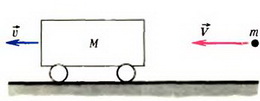
а
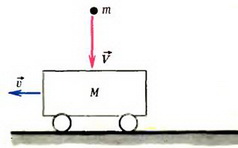
б
Рис. 1
Воспользуемся законом сохранения импульса в проекции на направление первоначального движения тележки.
В случае а) получим:
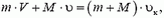
откуда конечная скорость тележки
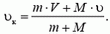
Как видно, после попадания пули скорость тележки увеличилась.
В случае б) начальный импульс пули не дает проекции на горизонтальное направление, следовательно,
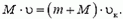
Отсюда
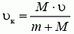
— конечная скорость тележки уменьшилась.
Векторный характер закона сохранения импульса в ряде случаев приводит к неожиданным результатам.
Задача 2. Две одинаковые лодки, в которых находятся два одинаковых спортсмена, движутся по инерции (почти без трения) с одинаковыми скоростями параллельно друг другу пи поверхности озера (рис. 2). Начинает идти дождь. Спортсмен, сидящий в первой лодке, вычерпывает воду из лодки и выливает ее в сторону, а спортсмен во второй лодке спит. Какая из лодок быстрее пройдет одно и то же расстояние? В направлении, перпендикулярном к килю, лодки двигаться не могут.

Рис. 2
Как следует из решения задачи 1, при попадании в лодку воды массой m, начальная скорость которой направлена вертикально (дождь!), скорость лодки уменьшается и становится равной по модулю
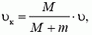
где M — масса лодки, υ — модуль ее начальной скорости. Отсюда видно, что изменение скорости лодки
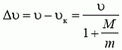
тем меньше, чем больше отношение M/m. Поскольку масса дождя, попавшего в лодки, одна и та же, уменьшение скорости будет большим у той лодки, из которой спортсмен вычерпывает воду. Заметим также, что при выбросе воды в сторону скорость лодки не меняется, так как киль не дает ей двигаться в перпендикулярном направлении.
Таким образом, вторая лодка, в которой спортсмен спит, быстрее пройдет заданное расстояние и первой окажется у финиша.
Если система незамкнутая, изменение ее импульса всегда связано с действием внешних сил.
Задача 3. Пучок частиц, имеющих скорость 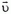 и массу m, падает на пластину площадью S; при этом он частично поглощается, а частично упруго отражается (рис. 3). Какая сила действует на пластину, если концентрация частиц в пучке равна n, а доля поглощенных частиц α? Рассмотреть также случай, когда пластина сама движется со скоростью
и массу m, падает на пластину площадью S; при этом он частично поглощается, а частично упруго отражается (рис. 3). Какая сила действует на пластину, если концентрация частиц в пучке равна n, а доля поглощенных частиц α? Рассмотреть также случай, когда пластина сама движется со скоростью 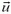 : а) навстречу пучку, б) в том же направлении, что и налетающие частицы.
: а) навстречу пучку, б) в том же направлении, что и налетающие частицы.
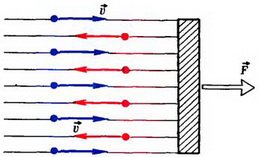
Рис. 3.
Вначале рассмотрим случай неподвижной пластины. Каждая частица, поглощаемая пластиной, передает ей импульс 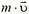 . За время Δt до пластины долетают те частицы, которые находятся в объеме
. За время Δt до пластины долетают те частицы, которые находятся в объеме 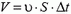 (υ — модуль скорости частиц), то есть
(υ — модуль скорости частиц), то есть
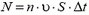 частиц.
частиц.
Из них поглощается
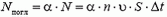 частиц.
частиц.
и, следовательно, пластине передается импульс
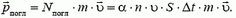
В соответствии с формулой (1) на пластину действует сила 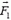 , модуль которой равен
, модуль которой равен
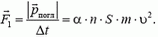
При упругом отражении частицы модуль ее скорости, а значит, и модуль импульса частицы не меняются, однако направление вектора импульса меняется на противоположное. Поэтому изменение импульса частицы
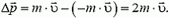
Число частиц, отраженных от пластины за время Δt, равно
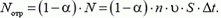
Следовательно, при отражении частиц пластине передается импульс
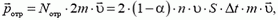
что приводит к появлению силы 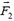 , действующей на пластину. Ее модуль
, действующей на пластину. Ее модуль
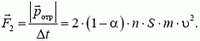
Полная сила, действующая на пластину, равна по модулю
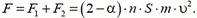 (3)
(3)
Для того чтобы найти силу, действующую на движущуюся пластину, перейдем в систему координат, движущуюся со скоростью 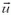 . В этой системе скорость частиц увеличивается при движении пластины навстречу пучку:
. В этой системе скорость частиц увеличивается при движении пластины навстречу пучку: 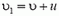 и уменьшается при движении пластины в обратном направлении:
и уменьшается при движении пластины в обратном направлении: 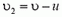 (здесь υ, u, υ1 и υ2 — модули соответствующих скоростей). В остальном все остается таким же, как в случае неподвижной пластины. Следовательно, сила, действующая на пластину, находится по формуле (3), в которой следует υ заменить на υ1 или υ2:
(здесь υ, u, υ1 и υ2 — модули соответствующих скоростей). В остальном все остается таким же, как в случае неподвижной пластины. Следовательно, сила, действующая на пластину, находится по формуле (3), в которой следует υ заменить на υ1 или υ2:
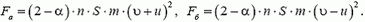
В первом случае сила возрастает, во втором—уменьшается.
Особый интерес представляет случай возникновения так называемой реактивной силы 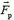 , когда из системы с некоторой скоростью
, когда из системы с некоторой скоростью 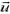 выбрасывается часть Δm ее массы. В соответствии с формулой (2)
выбрасывается часть Δm ее массы. В соответствии с формулой (2)
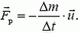
Величину 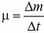 , равную массе вещества, выбрасываемого за единицу времени, называют обычно расходом вещества.
, равную массе вещества, выбрасываемого за единицу времени, называют обычно расходом вещества.
Задача 4. В воздушном шарике, удерживаемом нитью, в том месте, где крепится нить, появилось отверстие сечением S (рис. 4). Как изменилось натяжение нити, если скорость истечения газа из шарика равна υ? Плотность газа ρ.
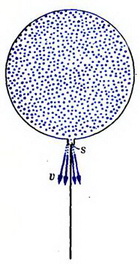
Рис. 4.
Изменение 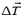 натяжения нити равно по модулю реактивной силе, возникающей при вытекании газа из шарика (изменением выталкивающей силы и веса шарика в начальный момент, пока изменение объема шарика мало, можно пренебречь). За время Δt вытекает объем газа
натяжения нити равно по модулю реактивной силе, возникающей при вытекании газа из шарика (изменением выталкивающей силы и веса шарика в начальный момент, пока изменение объема шарика мало, можно пренебречь). За время Δt вытекает объем газа 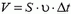 , его масса
, его масса 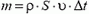 . Следовательно, расход газа
. Следовательно, расход газа 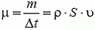 и реактивная сила
и реактивная сила
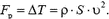
Задача 5. Закрепленный воздушный вентилятор потребляет мощность N, его КПД равен η. Какая реактивная сила действует на вентилятор во время его работы? Диаметр лопастей вентилятора D, плотность воздуха ρ.
Обозначим через υ модуль скорости воздушного потока, создаваемого вентилятором. Тогда масса воздуха, приводимого в движение за время Δt, равна 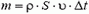 , где
, где 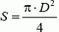 — площадь сечения воздушного потока (рис. 5), а его кинетическая энергия —
— площадь сечения воздушного потока (рис. 5), а его кинетическая энергия —
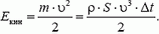
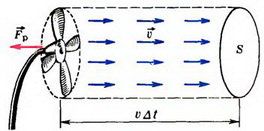
Рис. 5
Следовательно, мощность вентилятора
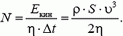
Отсюда можно найти скорость потока воздуха:
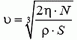
и реактивную силу, действующую на вентилятор:
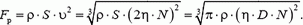
Если механическая система движется с постоянной скоростью, так что изменение ее импульса происходит только вследствие выброса массы, для нахождения реактивной силы удобнее перейти в систему отсчета, связанную с движущимся телом.
Задача 6. На горизонтальной поверхности стоит сосуд с водой, закрытый легким подвижным поршнем, на котором лежит тяжелый груз массой M (рис. 6). У дна сосуда имеется отверстие сечением s, через которое вытекает вода. Какова установившаяся скорость движения сосуда, если сила трения между сосудом и поверхностью пропорциональна скорости сосуда, причем коэффициент пропорциональности равен k. Площадь сечения сосуда S.
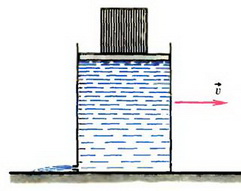
Рис. 6
Искомая скорость (точнее, ее модуль υ) определяется из условия равенства модулей силы трения и реактивной силы, действующей на сосуд:
Fтр = k·υ = Fp.
Чтобы найти реактивную силу, перейдем в систему отсчета, движущуюся со скоростью 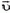 . В этом системе сосуд неподвижен. Для определения модуля u скорости истечения воды воспользуемся законом сохранения энергии.
. В этом системе сосуд неподвижен. Для определения модуля u скорости истечения воды воспользуемся законом сохранения энергии.
При вытекании небольшого количества воды массой Δm изменение кинетической энергии воды 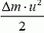 равно изменению потенциальной энергии воды Δm·g·h (h — высота уровня воды в сосуде) и груза M·g·Δh (Δh — перемещение груза, равное изменению уровня воды):
равно изменению потенциальной энергии воды Δm·g·h (h — высота уровня воды в сосуде) и груза M·g·Δh (Δh — перемещение груза, равное изменению уровня воды):
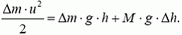
Изменение уровня воды в сосуде Δh выражается через массу Δm вытекающей воды: 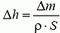 . Подставляя это выражение в закон сохранения энергии и сокращая на Δm, для скорости u истечения воды получим
. Подставляя это выражение в закон сохранения энергии и сокращая на Δm, для скорости u истечения воды получим
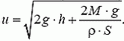
Если груз достаточно тяжелый (то есть его масса много больше массы воды в сосуде: 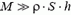 ), первым слагаемым под корнем можно пренебречь. В таком случае скорость истечения воды практически постоянна, и равна
), первым слагаемым под корнем можно пренебречь. В таком случае скорость истечения воды практически постоянна, и равна
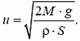
Теперь можно найти реактивную силу, действующую на сосуд:
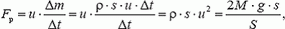
и скорость движения сосуда:
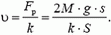
Задача 7. Из ракеты массой М, движущейся со скоростью 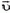 , выбрасывается порция топлива m со скоростью
, выбрасывается порция топлива m со скоростью 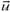 относительно ракеты. Какой станет скорость ракеты? Какую скорость будет иметь ракета после выброса двух таких порций, трех порций, k порций (рис. 7)?
относительно ракеты. Какой станет скорость ракеты? Какую скорость будет иметь ракета после выброса двух таких порций, трех порций, k порций (рис. 7)?
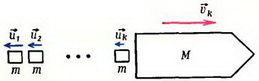
Рис. 7.
Воспользуемся законом сохранения импульса. Удобнее написать его в системе отсчета, движущейся с первоначальной скоростью ракеты 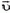 (так как скорость выброса топлива
(так как скорость выброса топлива 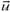 задана относительно ракеты). В проекции на направление движения ракеты получим
задана относительно ракеты). В проекции на направление движения ракеты получим
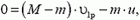
откуда скорость ракеты
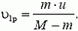
В неподвижной системе отсчета скорость ракеты после выброса первой порции топлива равна по модулю
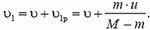
Выброс второй порции топлива будем рассматривать в системе, движущейся со скоростью 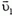 (на рисунке 7 выброс топлива показан в неподвижной системе отсчета). Из закона сохранения импульса имеем
(на рисунке 7 выброс топлива показан в неподвижной системе отсчета). Из закона сохранения импульса имеем
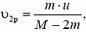
а в неподвижной системе
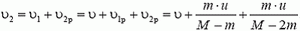
Легко видеть, что после k выбросов скорость ракеты будет равна
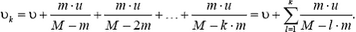
Для сравнения найдем также скорость ракеты 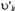 при одноразовом выбросе топлива массой k·m с той же скоростью
при одноразовом выбросе топлива массой k·m с той же скоростью 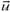 относительно ракеты. Для этого опять воспользуемся законом сохранения импульса, только запишем его сразу относительно неподвижной системы отсчета:
относительно ракеты. Для этого опять воспользуемся законом сохранения импульса, только запишем его сразу относительно неподвижной системы отсчета:
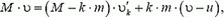
откуда
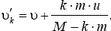
Легко видеть, что 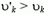 . Такой результат связан с предположением, что скорость выброса топлива из ракеты в неподвижной системе отсчета постоянна и равна υ – u. В действительности по мере ускорения ракеты скорость выброса топлива уменьшается (постоянна скорость выброса относительно ракеты). Поэтому первая формула для υk более точно описывает реальную ситуацию.
. Такой результат связан с предположением, что скорость выброса топлива из ракеты в неподвижной системе отсчета постоянна и равна υ – u. В действительности по мере ускорения ракеты скорость выброса топлива уменьшается (постоянна скорость выброса относительно ракеты). Поэтому первая формула для υk более точно описывает реальную ситуацию.
Упражнения
1. Нейтрон массой m0 поглощается ядром неподвижного атома массой m. Известно, что энергия возбужденного атома может отличаться от энергии основного состояния только на определенное значение Е0. С какой скоростью двигался нейтрон?
2. Ракета, запущенная вертикально вверх, взрывается в высшей точке своего подъема. При взрыве образуются три осколка равной массой. Один осколок падает в месте старта ракеты. Два других падают на Землю в один и тот же момент. Показать, что эти осколки приземляются на одном и том же расстоянии от места старта ракеты.
3. С какой силой давит на землю кобра, когда она, готовясь к прыжку, поднимается вертикально со скоростью 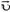 ? Масса змеи М, ее длина L.
? Масса змеи М, ее длина L.
4. Лестница, на которой находится человек, уравновешена противовесом на веревке, перекинутой через блок. Масса человека равна массе лестницы, а масса блока и трение пренебрежимо малы. Человек, находящийся вначале на высоте h от пола, поднимается по лестнице на n ступенек. На какой высоте от пола он окажется после этого, если расстояние между ступеньками равно l?
5. На конце соломинки, лежащей на гладком столе, сидит кузнечик. С какой наименьшей скоростью он должен прыгнуть, чтобы попасть на другой конец соломинки? Трение между столом и соломинкой отсутствует. Масса соломинки М, ее длина l. Масса кузнечика m.
6. Скорость истечения газов из сопла ракеты равна 300 м/с относительно ракеты. Может ли такой двигатель разогнать ракету до скорости 600 м/с?
7. При испытании реактивного снаряда, установленного в хвосте самолета для защиты его от нападения сзади, был обнаружен удивительный факт: при пуске снаряд разворачивался и догонял самолет. Как можно объяснить это явление?
Ответы
1. 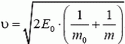
2. Указание. Воспользуйтесь законом сохранения импульса.
3. 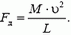
4. 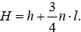
5. 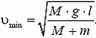
6. Может (реактивная сила определяется значением скорости истечения газов относительно ракеты).
7. Непосредственно после вылета из ракеты снаряд движется в ту же сторону, что и ракета, то есть вперед. Через некоторое время стабилизаторы разворачивают снаряд, затем под действием реактивной силы он разгоняется и может догнать самолет.
| Выложил | alsak |
| Опубликовано | 25.03.09 |
| Просмотров | 14175 |
| Рубрика | Решение задач |
| Тема | Законы сохранения |