Жорина Л., Черноуцан А.И. Решение задач с распределенной силой // Квант
Жорина Л., Черноуцан А.И. Решение задач с распределенной силой // Квант. — 2004. — № 6. — С. 36-38.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
При решении задач из различных разделов физики приходится встречаться с ситуациями, когда силы непрерывно распределены вдоль какой-нибудь линии или поверхности. Обычно требуется найти или равнодействующую этих сил, или возникающие в объекте их приложения (линейном или плоском) натяжения и деформации.
При решении таких задач удобно использовать один из двух подходов. В первом подходе — назовем его дифференциальным — анализируют силы, действующие на маленький элемент линии или поверхности, при этом размер этого элемента в окончательный ответ не входит. Во втором — инmегральном — подходе производят суммирование по всем элементам, опираясь при этом на симметрию системы и стараясь избежать прямого интегрирования. Впрочем, как мы увидим, эти подходы тесно друг с другом связаны.
Начнем с рассмотрения линейных объектов.
Задача 1. Точечный заряд q находится в центре кольца радиусом R, по которому равномерно распределен одноименный заряд Q. Найдите силу натяжения кольца. Взаимодействие зарядов кольца друг с другом не учитывать.
Разберем два способа решения этой задачи.
Способ 1. Запишем условие равновесия элемента кольца, видного из центра под маленьким углом Δα (рис. 1).
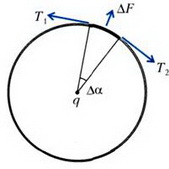
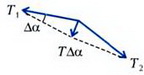
Рис. 1.
Заряд этого элемента равен 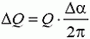 , на него действует сила отталкивания
, на него действует сила отталкивания ![]() от заряда qи две одинаковые по модулю силы натяжения
от заряда qи две одинаковые по модулю силы натяжения 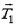 и
и 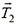 (T1 = T2 = Τ), угол между которыми равен
(T1 = T2 = Τ), угол между которыми равен ![]() . Равнодействующая сил натяжения (с учетом малости Δα) составляет
. Равнодействующая сил натяжения (с учетом малости Δα) составляет ![]() , и условие равновесия этого элемента принимает вид
, и условие равновесия этого элемента принимает вид
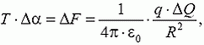 или
или 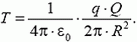
Способ 2. Рассмотрим силы, приложенные к полукольцу (рис. 2).
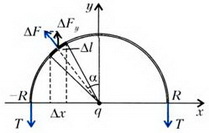
Рис. 2.
На него действуют две параллельные силы натяжения. Их сумма, равная 2T, уравновешивается равнодействующей всех электростатических сил, приложенных к различным элементам полукольца. Из симметрии системы очевидно, что равнодействующая электростатических сил направлена по оси у. Получаем
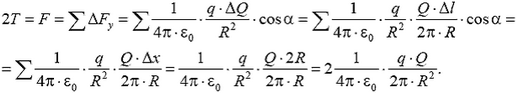
Смысл приведенного расчета состоит в следующем: вместо того чтобы брать проекцию силы, приложенной к элементу кольца, на ось у, мы заменили этот элемент его проекцией на ось х: ![]() . Мы как бы «выпрямили» полуокружность, после чего все силы стали параллельны друг другу. Отметим, что, в соответствии с третьим законом Ньютона, мы одновременно вычислили силу, действующую на точечный заряд qсо стороны полукольца, т.е. нашли напряженность поля, создаваемую полукольцом с зарядом
. Мы как бы «выпрямили» полуокружность, после чего все силы стали параллельны друг другу. Отметим, что, в соответствии с третьим законом Ньютона, мы одновременно вычислили силу, действующую на точечный заряд qсо стороны полукольца, т.е. нашли напряженность поля, создаваемую полукольцом с зарядом 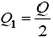 в своем центре:
в своем центре:
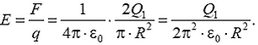
На первый взгляд, второй способ решения выглядит более громоздким и искусственным. Однако в некоторых случаях, особенно при вычислении равнодействующей силы, он имеет определенные преимущества.
Задача 2. Плоский контур расположен в однородном магнитном поле с индукцией В перпендикулярно линиям индукции. По контуру течет ток силой I. Найдите натяжение провода контура в двух случаях: а) контур имеет форму окружности радиусом R; б) контур имеет форму эллипса с полуосями a и b. Во втором случае следует найти натяжение в точках пересечения эллипса с осями. Силой магнитного взаимодействия частей контура пренебречь.
Первый случай очень похож на задачу 1, и его можно решать любым из двух способов. При решении первым способом получаем уравнение, связывающее силу натяжения провода с магнитной силой (силой Ампера), действующей на контур со стороны магнитного поля:
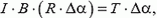
откуда
Однако ясно, что такое решение не применимо к контуру в форме эллипса. Что же касается второго подхода, то он применим как в первом, так и во втором случаях.
Чтобы найти натяжение провода в точках А и С эллипса (рис. 3), надо вычислить магнитную силу ![]() , действующую на примыкающую к этим точкам половину эллипса.
, действующую на примыкающую к этим точкам половину эллипса.
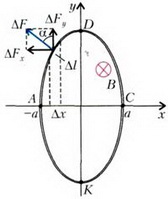
Рис. 3.
Проекции этой силы на оси x и yравны, соответственно,
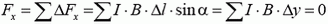
и
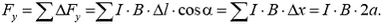
Поскольку магнитная сила равна двум силам натяжения, получаем
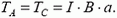
Аналогично найдем натяжение провода в точках D и К:
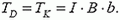
Можно заметить, что такой же расчет применим к участку контура любой формы. Сформулируем утверждение: сила, действующая со стороны однородного магнитного поля на участок контура с током любой формы, соединяющий какие-то две точки, равна силе, действующей на соединяющий эти точки прямой провод с таким же током. Физический смысл этого утверждения состоит в том, что полная сила, действующая на замкнутый контур с током со стороны однородного магнитного поля, должна быть равна нулю (иначе бы нарушался закон сохранения энергии).
Задача 3. Тонкое кольцо массой m и радиусом R вращается вокруг своей оси с угловой скоростью ω. Найдите натяжение кольца.
Запишем второй закон Ньютона для малого элемента кольца. Равнодействующая двух сил натяжения сообщает этому элементу центростремительное ускорение:
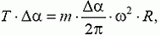
откуда
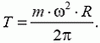
Это решение аналогично первому, т.е. дифференциальному, подходу в статических задачах. А применим ли в этом случае интегральный подход? Если мы запишем второй закон Ньютона для половины кольца, то в формулу для центростремительного ускорения центра масс полукольца войдет расстояние rц от центра масс до оси:
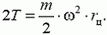
Если бы мы знали rц, то нашли бы натяжение Τ вторым способом. Однако можно использовать это уравнение именно для вычисления rц: подставив сюда T, вычисленное первым способом, получим
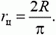
Задача 4. Тонкое алюминиевое кольцо радиусом R = 10 см вращается вокруг своей оси. При какой угловой скорости кольцо разорвется, если разрыв происходит при механическом напряжении σκρ = 2•107 Н/м2. Плотность алюминия ρ = 2700 кг/м3.
Условие разрыва кольца запишем в виде
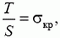
где Τ — натяжение кольца, S — площадь сечения. Подставим Τ из решения предыдущей задачи и учтем, что 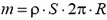 .
.
Получим
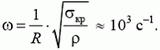
Интересно, что ответ не зависит от толщины кольца.
Перейдем теперь к рассмотрению не линейных, а плоских объектов. Обычно в этих задачах удобнее применять второй (интегральный) подход. Однако попробуйте самостоятельно решить их и с помощью дифференциального метода.
Задача 5. Внутри тонкой сферы радиусом R создано избыточное давление р. Какой должна быть толщина сферы, чтобы она при этом не разорвалась, если разрыв происходит при напряжении σκρ?
Из условия равновесия полусферы следует, что сила упругости в диаметральном сечении равна равнодействующей сил давления:
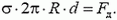
Для вычисления равнодействующей сил давления отметим, что она направлена вдоль оси симметрии полусферы (рис. 4):
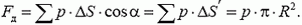
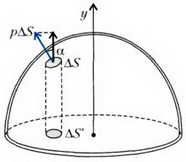
Рис. 4.
Как и в задачах 1 и 2, мы, вместо того чтобы проецировать силу на ось симметрии, взяли проекцию площади площадки ΔS на плоскость, на которую опирается полусфера (т.е. как бы «выпрямили» полусферу). Подставив в предыдущую формулу, получим
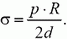
Из условия σ < σκρ найдем
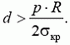
Обратите внимание на близкую аналогию этой задачи с задачей вычисления избыточного давления под искривленной поверхностью жидкости, возникающего вследствие поверхностного натяжения (так называемое лапласово давление). В этом случае условие равновесия поверхностной пленки имеет вид
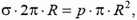
где σ в данном случае — коэффициент поверхностного натяжения жидкости. Отсюда получаем
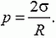
Аналогично случаю линейных объектов (см. задачу 2), расчет равнодействующей сил давления можно обобщить на поверхность любой формы. Обобщение выглядит так: если давление постоянно, то равнодействующая сил давления, действующих на произвольную поверхность, опирающуюся на плоский участок, равна силе давления, приложенной к этому участку. Физический смысл этого утверждения состоит в том, что полная сила давления на замкнутую поверхность равна нулю (если давление постоянно).
Умение увидеть физический смысл рассчитываемой величины позволяет иногда заметно упростить задачу, которая изначально выглядит сложной.
Задача 6. Тонкий полусферический колокол радиусом R стоит на горизонтальной поверхности. Через маленькое отверстие в верхней точке колокол заполняют водой. Чему равна масса колокола, если в тот момент, когда вода полностью заполнила колокол, она начала из под него вытекать?
Условие отрыва колокола от горизонтальной поверхности сводится к тому, что равнодействующая сил давления, действующих на него со стороны воды, равна его силе тяжести:
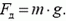
Прямое вычисление равнодействующей сил давления сложнее, чем в предыдущей задаче. Поскольку давления в разных точках колокола разные, избежать интегрирования в прямом расчете не удается. Однако если заметить, что искомая сила давления приложена не только к колоколу, но и к воде, то ее можно найти из условия равновесия объема воды:
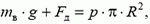
где 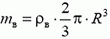 — масса воды,
— масса воды, 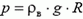 — давление воды на горизонтальную поверхность. Окончательно получаем
— давление воды на горизонтальную поверхность. Окончательно получаем
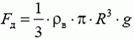
или
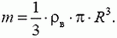
Задача 7. Вычислите напряженность электрического поля в центре полусферы радиусом R, по поверхности которой равномерно распределен заряд Q.
Как отмечалось в задаче 1, такая задача идентична задаче о силе, действующей на заряженную полусферу со стороны точечного заряда, помещенного в ее центр. Однако в данном случае мы проведем расчет непосредственно для напряженности.
Поскольку напряженность направлена вдоль оси симметрии полусферы, то возьмем проекцию на это направление от напряженности, создаваемой маленьким участком полусферы площадью ΔS:
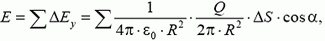
где 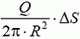 — заряд этого участка. Так как
— заряд этого участка. Так как 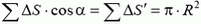 , получаем
, получаем
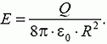
Задача 8. Проводящая сфера радиусом R заряжена зарядом Q. С какой силой отталкиваются друг от друга две половинки сферы?
Вычислим силу, действующую на маленький участок поверхности площадью ΔS . Эта сила равна
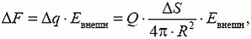
где Евнеш — напряженность поля, создаваемого внешними (по отношению к данному участку) зарядами сферы. Чтобы найти Евнеш, заметим, что полная напряженность среды вблизи поверхности равна (рис. 5)

где 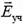 — напряженность собственного поля участка сферы.
— напряженность собственного поля участка сферы.
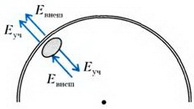
Рис. 5.
По разные стороны выделенного участка векторы 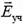 направлены в противоположные стороны (вблизи центра участка напряженность совпадает с напряженностью поля равномерно заряженной плоскости), а векторы
направлены в противоположные стороны (вблизи центра участка напряженность совпадает с напряженностью поля равномерно заряженной плоскости), а векторы 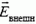 направлены одинаково. Поскольку внутри сферы напряженность равна нулю, то
направлены одинаково. Поскольку внутри сферы напряженность равна нулю, то
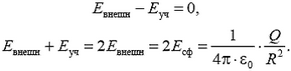
Тогда получаем
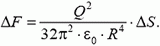
Следовательно, внутри заряженной сферы как бы существует давление
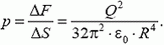
Как было показано в задаче 5, сила, действующая на полусферу, равна
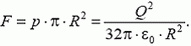
Заметим, что формула для давления может быть получена и из энергетических соображений. Мысленно уменьшая радиус сферы на ΔR, мы совершим работу против силы давления, равную
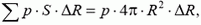
которая равна изменению электростатической энергии
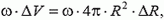
где ω — объемная плотность энергии. Видно, что электростатическое давление на металлическую поверхность отрицательно (направлено в сторону поля) и равно объемной плотности энергии поля:
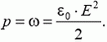
Упражнения
1. Резиновое кольцо массой m и радиусом R0 раскрутили вокруг его оси до угловой скорости ω. Найдите новый радиус кольца, если жесткость резины k.
2. Петлю из резинового шнура длиной l0 положили на пленку жидкости. Пленку прокололи внутри петли, в результате чего она растянулась в окружность длиной l. Считая известной жесткость резины k, определите коэффициент поверхностного натяжения жидкости.
3. По длинному соленоиду радиусом R течет ток силой I. При этом индукция магнитного поля соленоида равна В. Найдите силу натяжения провода соленоида. Указание: учтите отличие внешнего поля от поля самого соленоида (см. задачу 8).
4. Тонкостенный цилиндр длиной l и радиусом R заполнили газом под давлением р. Найдите силу взаимодействия двух половинок цилиндра, если его мысленно разрезать плоскостью: а) перпендикулярной оси цилиндра, б) проходящей через ось цилиндра.
Ответы
1. 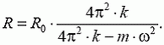
2. 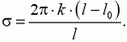
3. 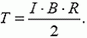
4. а) 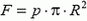 ; б)
; б) 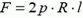 .
.
| Выложил | alsak |
| Опубликовано | 02.05.09 |
| Просмотров | 17497 |
| Рубрика | Решение задач |
| Тема | Динамика |