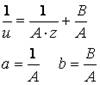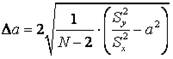Слободянюк А.И. Метод наименьших квадратов в школьном физическом эксперименте
Слободянюк А.И. Метод наименьших квадратов в школьном физическом эксперименте // Фiзiка: праблемы. выкладання.– 1995. – Вып. 1. – С. 88-99.
К настоящему времени разработано несколько методов обработки результатов измерений. Наиболее употребительным и точным является метод наименьших квадратов (МНК).
В статье излагается суть метода наименьших квадратов, условия его применимости. Авторы предлагают примеры использования метода МНК.
Как правило, все физические эксперименты сводятся к измерению зависимости некоторой величины u от одной или нескольких других величин z1, z2, …, zn.
Необходимость получения зависимости (а не проведения «точечного» измерения при фиксированных значениях параметров) оправдывается следующими преимуществами:
- возможностью проверки теоретических построений;
- возможностью исключения трудноопределяемых параметров;
- в некоторых случаях более простым способом оценки погрешностей.
К настоящему времени разработано несколько методов обработки результатов измерений. Наиболее употребительным, простым и обоснованным является метод наименьших квадратов (МНК).
1. Суть метода наименьших квадратов, условия его применимости
Допустим, нам известен вид функциональной зависимости физической величины u от другой физической величины z, но не известны параметры этой зависимости a, b, c,... ![]() . В результате проведенных измерений получена таблица значений ui при некоторых значениях
. В результате проведенных измерений получена таблица значений ui при некоторых значениях ![]() . Требуется найти такие значения параметров a, b, c,... при которых функция
. Требуется найти такие значения параметров a, b, c,... при которых функция ![]() наилучшим образом описывает экспериментальные данные.
наилучшим образом описывает экспериментальные данные.
МНК утверждает, что «наилучшей» кривой будет такая, для которой сумма квадратов отклонений экспериментальных значений uiот значений функции ![]() минимальна. Таким образом, для определения параметров a, b, c,... необходимо найти минимум функции
минимальна. Таким образом, для определения параметров a, b, c,... необходимо найти минимум функции
![]() . (1)
. (1)
Отметим, что Φ рассматривается здесь как функция параметров a, b, c,..., так как величины ui, zi известны из экспериментальных данных.
В общем случае нахождение минимума функции (1) удается сделать далеко не всегда. Поэтому для практической реализации МНК часто применяют следующий искусственный прием: находят некоторое функциональное преобразование ![]() , которое приводит исследуемую зависимость
, которое приводит исследуемую зависимость ![]() к линейному виду
к линейному виду
![]() (2)
(2)
для которого реализация МНК наиболее проста. Примеры преобразований такого типа приведены в табл. 1. Некоторые преобразования будут рассмотрены ниже при изложении конкретных примеров.
Подставим выражение (2) в выражение (1)
![]() (3)
(3)
и получим уравнения для определения параметров а и b. Для этого вычислим производные функции Φ по а и b и приравняем их к нулю,
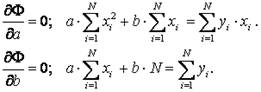 (4)
(4)
Данная система является линейной и легко решается:
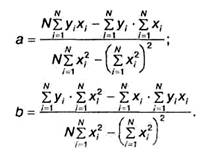 (5)
(5)
Однако полученные выражения не очень удобны для практических расчетов, поэтому перепишем их в несколько иной форме. Для этого обозначим
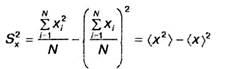 (6)
(6)
(угловые скобки ![]() означают среднее арифметическое по экспериментальным данным) и запишем
означают среднее арифметическое по экспериментальным данным) и запишем
![]() (7)
(7)
Из второго уравнения системы (4) выразим ![]() .
.
Выражения (6), (7) позволяют достаточно быстро с помощью непрограммируемого калькулятора рассчитать параметры линейной зависимости (2).
Сформулируем условия, при которых полученные таким способом значения параметров являются оптимальными (несмещенными, состоятельными, эффективными оценками [1]).
1. Результаты измерений являются независимыми.
2. Погрешности измерений подчиняются нормальному распределению.
3. Величины хi, известны точно.
Практически МНК в изложенной форме применяют, если погрешности измерений уi значительно (более чем на порядок) превосходят погрешности измерений величин xi.
При выполнении этих условий параметры а, b линейно выражаются через результаты измерений уi, (погрешностями измерений xi пренебрегаем), поэтому погрешность определения параметров может быть найдена стандартным методом как погрешность косвенного измерения. Несколько громоздкие выкладки приводят к следующим формулам для оценок погрешностей:
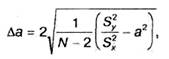 (8)
(8)
где ![]() , остальные обозначения сохраняем прежними:
, остальные обозначения сохраняем прежними:
![]() (9)
(9)
Таким образом, формулы (6) – (9) полностью исчерпывают МНК для анализа линейной зависимости. Формулы (7) – (8) дают оценки только случайных погрешностей измерений. Их использование полностью оправдано, если этот тип погрешностей преобладает, что чаще всего бывает на практике. Свидетельством такого преобладания является заметный разброс точек (уi, хi) на графике, когда эти точки не ложатся точно на прямую. Отметим, что постоянная систематическая приборная погрешность не влияет на определение параметра а и является аддитивной добавкой к погрешности параметра b, т.е. если приборная погрешность измерения величин уi равна ![]() , то
, то ![]() .
.
Отметим также, что в некоторых случаях необходимо проводить несколько измерений величины u при одном и том же значении z. В этом случае никаких модификаций МНК не требуется. Достаточно рассматривать эти значения как независимые, т.е. включать в расчеты пары zi, ui·с одними и теми же значениями zi. Иными словами, одному значению z может соответствовать несколько значений u. Естественно, не могут быть все z одинаковыми, иначе в формуле (5) в знаменателе окажется нуль.
2. Практическая реализация МНК для линейной зависимости на непрограммируемом калькуляторе
Как показывает опыт, лучше всего для расчетов параметров линейной зависимости и их погрешностей воспользоваться заранее приготовленным бланком (табл. 2). В колонке 1 записываются номера проведенных измерений (i = 1, 2, ..., Ν); в колонках 2, 3 – результаты измерений величин zi, ui.
Первым шагом использования этого бланка для реализации МНК является заполнение колонок 4, 5. В них представляются результаты преобразований от z, u к величинам х, у, между которыми ищется линейная зависимость.
Расчетные формулы, представленные в колонке 6, допускают вычисления на калькуляторе без записи промежуточных результатов. Любой, даже самый простейший калькулятор, имеет одну ячейку памяти, в которой можно накапливать значения сумм. Расчеты следует проводить в такой последовательности:
1) вычислить ![]() – для этого последовательно ввести в память все значения хi, записанные в колонке 4, и после этого содержимое разделить на число пар измерений N, результат записать в колонке 7;
– для этого последовательно ввести в память все значения хi, записанные в колонке 4, и после этого содержимое разделить на число пар измерений N, результат записать в колонке 7;
2) вычислить ![]() , последовательно набирая значения xi, накопить в памяти сумму их квадратов (набрать значения – «умножить» – «равно» – «в память +») и разделить на N, от полученного результата вычесть квадрат среднего, результат записать в колонке 7;
, последовательно набирая значения xi, накопить в памяти сумму их квадратов (набрать значения – «умножить» – «равно» – «в память +») и разделить на N, от полученного результата вычесть квадрат среднего, результат записать в колонке 7;
3 – 4) аналогично вычислить ![]() и
и ![]() ;
;
5) в памяти накопить сумму произведений ![]() , разделить на N, вычесть произведение средних
, разделить на N, вычесть произведение средних ![]() и разделить на
и разделить на ![]() – получить значение параметра а.
– получить значение параметра а.
Дальнейшие расчеты вполне очевидны.
3. Пример использования МНК
Задача. С помощью математического маятника измерить ускорение свободного падения.
Оборудование: нить, грузик, штатив, линейка, секундомер.
Решение. Период малых колебаний математического маятника Т определяется по формуле ![]() . Эту формулу можно преобразовать к виду
. Эту формулу можно преобразовать к виду ![]() .
.
Иными словами, между длиной маятника l и квадратом периода существует линейная связь, которую мы запишем в виде: ![]() , где
, где ![]() (преобразование к линейному виду). Введение параметра b в данном случае не является обязательным, так как теоретически b= 0. Однако запись линейной зависимости в общем виде позволяет учесть автоматически погрешность в определении длины маятника, более того, в этом случае можно измерять не длину маятника, а только ее изменение. Если же все измерения проведены корректно, то МНК должен привести к результату
(преобразование к линейному виду). Введение параметра b в данном случае не является обязательным, так как теоретически b= 0. Однако запись линейной зависимости в общем виде позволяет учесть автоматически погрешность в определении длины маятника, более того, в этом случае можно измерять не длину маятника, а только ее изменение. Если же все измерения проведены корректно, то МНК должен привести к результату ![]() , что и будет свидетельствовать о том, что
, что и будет свидетельствовать о том, что ![]() .
.
Результаты измерений изменения длины маятника Δl (измерялось расстояние от точки подвеса до некоторой фиксированной точки на нити) и времени t двадцати колебаний (измерено с помощью ручных часов) приведены в табл. 3. Там же представлены результаты расчетов по изложенной методике.
Вычислив коэффициент а, можно найти значение ускорения свободного падения ![]() и его погрешность
и его погрешность ![]() .
.
Окончательный результат ![]() м/с.
м/с.
Значение параметра b не использовалось (смысл полученной величины – расстояние от фиксированной точки на нити до центра масс груза). Использование этого параметра оправдано сложностью точного определения положения центра тяжести.
4. Экспериментальные задачи, предполагающие использование МНК
В заключение предложим несколько экспериментальных задач, для решения которых следует использовать изложенный метод. Каждая задача снабжена краткими указаниями к решению. Так как в каждом случае формулы для оценок погрешностей очевидны, то здесь они не приводятся.
Задача 1. Период колебаний математического маятника зависит от амплитуды j0 (в радианах) по закону
![]() (10)
(10)
Определите значение параметра β.
Оборудование: нить, груз, штатив, транспортир, электронный секундомер.
Указания к решению. Зависимость периода колебаний от амплитуды достаточно слабая. Чтобы ее обнаружить, необходимо проводить измерения с высокой точностью (–0,01 с), для чего требуется электронный секундомер.
Зависимость (10) представим в виде ![]() , где y = T,
, где y = T,![]() b = Т0. По МНК для линейной зависимости
b = Т0. По МНК для линейной зависимости ![]() можно найти значения параметров а и b, тогда искомый коэффициент определится по формуле
можно найти значения параметров а и b, тогда искомый коэффициент определится по формуле ![]() (отметим, что теоретическое значение
(отметим, что теоретическое значение ![]() ).
).
Задача 2. Определите фокусное расстояние собирающей линзы.
Оборудование: источник света, экран, линза, линейка.
Указания к решению. Воспользуемся формулой тонкой линзы
![]() (11)
(11)
где d – расстояние от предмета до линзы, f – расстояние от линзы до изображения, F – фокусное расстояние линзы.
Обозначим ![]() , тогда
, тогда ![]() . Если измерить несколько пар значений diи fiи нанести на график точки
. Если измерить несколько пар значений diи fiи нанести на график точки ![]() , то эти точки должны лечь на прямую, которая отсекает на осях х, у отрезки, численно равные
, то эти точки должны лечь на прямую, которая отсекает на осях х, у отрезки, численно равные ![]() . Если обработать эту зависимость по МНК, можно получить
. Если обработать эту зависимость по МНК, можно получить ![]() и затем найти
и затем найти ![]() .
.
Задача 3. Остывание воды описывается формулой ![]() , где ΔT–разность температур воды и воздуха в комнате, ΔT0 – эта же разность в момент времени t = 0. Определите, сколько времени прошло с момента кипения воды.
, где ΔT–разность температур воды и воздуха в комнате, ΔT0 – эта же разность в момент времени t = 0. Определите, сколько времени прошло с момента кипения воды.
Оборудование: горячая вода в сосуде, термометр, часы.
Указания к решению. Необходимо заранее закипятить воду и поставить ее остывать. Через некоторое время этот сосуд можно предоставить для выполнения задания. Следует иметь в виду, что время остывания стакана воды при комнатных условиях порядка 40 мин.
Для решения поставленной задачи необходимо измерить зависимость температуры воды T от времени t. Далее, перепишем приведенную формулу в виде ![]() , где T0 – комнатная температура, Tкип – температура кипения воды, t0 – время, прошедшее от закипания до начала измерения. Так как в. формулу входят только разности температур, то можно пользоваться шкалой Цельсия. Прологарифмируем последнее выражение
, где T0 – комнатная температура, Tкип – температура кипения воды, t0 – время, прошедшее от закипания до начала измерения. Так как в. формулу входят только разности температур, то можно пользоваться шкалой Цельсия. Прологарифмируем последнее выражение
![]() (12)
(12)
и обозначим ![]() , x= t, получим линейную зависимость
, x= t, получим линейную зависимость ![]()
Обрабатывая результаты измерений по МНК, найдем значения параметров а, b, из которых можно вычислить искомое значение времени t0: ![]() .
.
Задача 4. Исследуйте, как зависит сила сопротивления воздуха, действующая на падающие кусочки бумаги, от скорости последних.
Оборудование: кусочки бумаги , секундомер.
Указания к решению. Кусочки бумаги следует сделать квадратными (приблизительно ![]() см).и слегка изогнуть в виде «парашютиков», чтобы их падений было устойчивым. Отлично для этой же цели подходят одноразовые тарелочки, изготовленные из плотной бумаги или фольги.
см).и слегка изогнуть в виде «парашютиков», чтобы их падений было устойчивым. Отлично для этой же цели подходят одноразовые тарелочки, изготовленные из плотной бумаги или фольги.
Падение бумажных тарелочек (или парашютиков) происходит с постоянной скоростью, если пренебречь небольшим начальным этапом разгона. Сила сопротивления воздуха зависит от скорости uпо закону
![]() (13)
(13)
(требуется определить γ), при установившемся движении эта сила численно равна силе тяжести ![]() , следовательно, скорость установившегося движения
, следовательно, скорость установившегося движения ![]() , а время падения с высоты h:
, а время падения с высоты h:
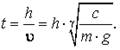 (14)
(14)
Возьмем несколько (1, 2, 3, ..., 5) одинаковых тарелочек и измерим время падения tn сложенных вместе n тарелочек. Коэффициент с в формуле (13) будет одинаков (он зависит только от формы тарелочки), масса же падающих тел ![]() , где m0 – масса одной тарелочки. Используем (14):
, где m0 – масса одной тарелочки. Используем (14): 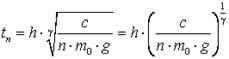 , в логарифмической форме
, в логарифмической форме
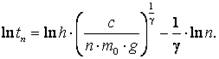 (15)
(15)
Как следует из этой формулы, между ![]() и
и ![]() существует линейная связь
существует линейная связь ![]() , где
, где ![]() , в b вошли все остальные постоянные величины, измерять которые нет необходимости.
, в b вошли все остальные постоянные величины, измерять которые нет необходимости.
Таким образом, измерив зависимость времени падения tn, от числа сложенных вместе n тарелочек и построив зависимость (15), по МНК можно найти значение параметра а и искомой величины ![]() .
.
При проведении эксперимента необходимо иметь в виду, что время падения кусочка бумаги ![]() см с высоты
см с высоты ![]() равно приблизительно 1,5 с, поэтому необходимо измерять время падения с погрешностью порядка 0,1 с. Следовательно, для каждого значения числа n нужно получить несколько значений tn. Подчеркнем, что в этой ситуации нет необходимости предварительно рассчитывать средние значения
равно приблизительно 1,5 с, поэтому необходимо измерять время падения с погрешностью порядка 0,1 с. Следовательно, для каждого значения числа n нужно получить несколько значений tn. Подчеркнем, что в этой ситуации нет необходимости предварительно рассчитывать средние значения ![]() , можно (и нужно) рассматривать все результаты измерения как независимые и включать их в бланк расчета.
, можно (и нужно) рассматривать все результаты измерения как независимые и включать их в бланк расчета.
Еще одна задача подобного типа подробно рассмотрена в журнале «Фокус» [3].
5. Заключение
Рассмотренный алгоритм расчетов по МНК апробирован на летних сборах в лагере «Зубренок». Проведенные с победителями олимпиад занятия показали, что этот метод вполне доступен школьникам старших классов с углубленным изучением физики. После приобретения навыка работы на микрокалькуляторе расчеты занимают приблизительно 5–10 мин.
Необходимость изучения методов графической обработки результатов (по MHK или другим) обосновывается участием команд республики на международных соревнованиях, (олимпиадах, турнирах юных физиков), где графические методы занимают главенствующее место и оцениваются весьма высоко.
1. Тэйлор Дж. Введение в теорию ошибок. – М: Мир , 1985.
2. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983.
3. Тимофеев А.. Проверим Стокса? – Фокус. – 1995. – №2. – С. 44-49.
Табл. 1.
Приведение к линейной зависимости
|
Вид зависимости |
Преобразование |
Параметры |
|
|
|
|
|
|
|
|
|
|
|
|
Табл. 2.
Бланк расчета параметров линейной зависимости
|
i |
z |
u |
x |
y |
Расчетные формулы |
Результаты |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
Табл. 3.
Определение параметров зависимости
периода колебаний маятника от его длины
|
Δl, см |
t, с |
|
|
Расчетные формулы |
Результаты |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
65 |
36 |
0,65 |
3,24 |
|
0.378 |
|
2 |
54 |
33 |
0,54 |
2,72 |
|
0.0393 |
|
3 |
37 |
29 |
0,37 |
2,10 |
|
2.14 |
|
4 |
21 |
25 |
0,21 |
1,56 |
|
0.593 |
|
5 |
11 |
21 |
0,11 |
1,10 |
|
3.88 |
|
|
0.678 |
|||||
|
|
0.22 |
|||||
|
|
0,094 |
![]()
| Выложил | alsak |
| Опубликовано | 26.12.07 |
| Просмотров | 51692 |
| Рубрика | Экспериментальные задачи | Решение задач |
| Тема | Без тем |