Ащеулов С., Барышев В. Погоня, столкновение, поимка // Квант
Ащеулов С., Барышев В. Погоня, столкновение, поимка // Квант. — 1979. — № 1. — С. 20-26.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Ровно в полдень часовая и минутная стрелки часов совпадают. Когда они совпадут в следующий раз? Несмотря на простоту, эта старая задача весьма поучительна. Решим ее.
Пусть ν1 и ν2 — частоты вращения часовой и минутной стрелок. Очевидно, 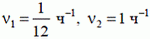 . Если t — момент времени следующего после полудня совпадения стрелок, то
. Если t — момент времени следующего после полудня совпадения стрелок, то 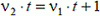 , ибо к моменту t минутная стрелка совершит на один оборот больше часовой. Следовательно,
, ибо к моменту t минутная стрелка совершит на один оборот больше часовой. Следовательно,
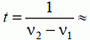 1 ч 5 мин 27 с.
1 ч 5 мин 27 с.
Мы видим, что величина t зависит лишь от разности частот 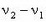 . Это наводит на мысль, что решение можно получить, рассуждая по-другому. За время между двумя последовательными совпадениями минутная стрелка совершает один оборот относительно часовой. Поскольку частота вращения минутной стрелки относительно часовой равна
. Это наводит на мысль, что решение можно получить, рассуждая по-другому. За время между двумя последовательными совпадениями минутная стрелка совершает один оборот относительно часовой. Поскольку частота вращения минутной стрелки относительно часовой равна 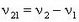 , можем сразу заключить, что
, можем сразу заключить, что
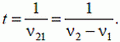
Эта задача относится к задачам следующего типа. В некоторой системе отсчета заданы характеристики движения нескольких тел. Требуется найти, как положения тел меняются друг относительно друга с течением времени. На этом занятии математического кружка мы познакомимся с несколькими такими задачами. Все они будут решены с помощью одного и того же примера: выбора подходящей системы координат.
1. Автомобили у перекрестка
Автомобили А и В движутся равномерно с одинаковыми скоростями по прямым дорогам 1 и 2, пересекающимся в точке О. Нужно определить кратчайшее расстояние между автомобилями, если известны их начальные положения  и угол α между дорогами (рис. 1 а).
и угол α между дорогами (рис. 1 а).
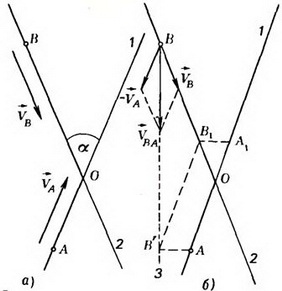
Рис. 1.
Рассмотрим движение автомобиля В с точки зрения наблюдателя, находящегося в автомобиле А. Как известно, скорость такого движения равна разности 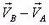 и постоянна по величине и направлению. Это значит, что автомобиль В движется относительно автомобиля А по некоторой прямой 3. (На рисунке 1 б прямая 3 изображена пунктиром; она нарисована в системе отсчета, связанной с автомобилем А.) Следовательно, автомобили находятся ближе всего друг к другу в тот момент, когда автомобиль В оказывается в точке В', являющейся основанием перпендикуляра, опущенного из точки А на прямую 3. Длина отрезка АВ' равна искомому кратчайшему расстоянию между автомобилями.
и постоянна по величине и направлению. Это значит, что автомобиль В движется относительно автомобиля А по некоторой прямой 3. (На рисунке 1 б прямая 3 изображена пунктиром; она нарисована в системе отсчета, связанной с автомобилем А.) Следовательно, автомобили находятся ближе всего друг к другу в тот момент, когда автомобиль В оказывается в точке В', являющейся основанием перпендикуляра, опущенного из точки А на прямую 3. Длина отрезка АВ' равна искомому кратчайшему расстоянию между автомобилями.
Чтобы изобразить положение отрезка АВ' в неподвижной системе отсчета, сместим его конец В' параллельно дороге 1 так, чтобы он попал в точку В1 на дороге 2, и проведем 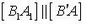 . Точки А1 и В1 являются искомыми положениями автомобилей (рис. 1 б).
. Точки А1 и В1 являются искомыми положениями автомобилей (рис. 1 б).
Очевидно, прямая 3 параллельна биссектрисе угла между дорогами. Нетрудно подсчитать, что
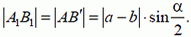
2. Охотник и лиса
Лиса бежит с постоянной скоростью 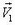 пo прямой l. Неподвижный охотник замечает лису, когда она находится в ближайшей от него точке прямой l (на расстоянии а). Как должён двигаться охотник, чтобы произвести выстрел с кратчайшего расстояния, если он может бежать со скоростью, равной по величине V2? Каково это кратчайшее расстояние?
пo прямой l. Неподвижный охотник замечает лису, когда она находится в ближайшей от него точке прямой l (на расстоянии а). Как должён двигаться охотник, чтобы произвести выстрел с кратчайшего расстояния, если он может бежать со скоростью, равной по величине V2? Каково это кратчайшее расстояние?
Нетрудно сообразить, что при условии 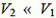 охотник должен бежать прямолинейно. Рассмотрим движение охотника в системе отсчета, связанной с лисой, т. е. движущейся со скоростью
охотник должен бежать прямолинейно. Рассмотрим движение охотника в системе отсчета, связанной с лисой, т. е. движущейся со скоростью 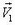 (рис. 2 а).
(рис. 2 а).
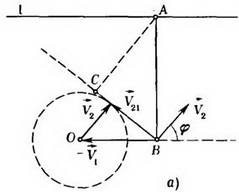
Рис. 2.
Скорость 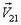 охотника в этой системе равна
охотника в этой системе равна 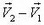 ,. Построим вектор
,. Построим вектор 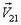 . Начало вектора
. Начало вектора 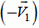 поместим в точку В (исходное положение охотника). Начало вектора
поместим в точку В (исходное положение охотника). Начало вектора 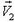 — в конец О вектора
— в конец О вектора 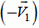 . Если начала всех векторов
. Если начала всех векторов 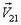 находятся в точке В, то их концы при всевозможных направлениях движения охотника лежат на окружности радиуса V2 с центром в точке О.
находятся в точке В, то их концы при всевозможных направлениях движения охотника лежат на окружности радиуса V2 с центром в точке О.
Во введенной системе отсчета прямая, по которой будет бежать охотник, должна иметь общие точки с этой окружностью и проходить как можно ближе к точке А.
Если 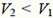 , то этим условиям удовлетворяет касательная, проведенная из точки В к окружности. В этом случае искомое направление движения охотника (угол φ; см. рис. 2 а) и кратчайшее расстояние до лисы Rmin таковы
, то этим условиям удовлетворяет касательная, проведенная из точки В к окружности. В этом случае искомое направление движения охотника (угол φ; см. рис. 2 а) и кратчайшее расстояние до лисы Rmin таковы 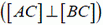
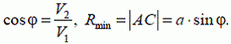
Если 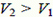 , то охотник может бежать в пределах заштрихованного сектора в любом направлении, если движется прямолинейно (рис. 2 б): условия задачи не запрещают охотнику достичь какой-то точки лисьей тропы раньше, чем через эту точку пробежит лиса, и в этом месте спокойно подождать лису.
, то охотник может бежать в пределах заштрихованного сектора в любом направлении, если движется прямолинейно (рис. 2 б): условия задачи не запрещают охотнику достичь какой-то точки лисьей тропы раньше, чем через эту точку пробежит лиса, и в этом месте спокойно подождать лису.
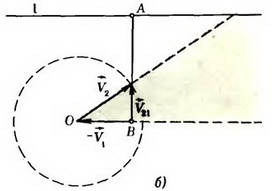
Рис. 2.
(*При условии 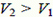 возможны и криволинейные траектории движения охотника. Семейство этих траекторий можно описать, например, следующим образом. Пусть наперед задано любое положительное число t. Тогда в течение интервала времени от начала движения до момента t охотник может бежать по любой траектории; начиная с момента t охотник может двигаться по любой из бесчисленного множества прямолинейных траекторий, удовлетворяющих условиям задачи.)
возможны и криволинейные траектории движения охотника. Семейство этих траекторий можно описать, например, следующим образом. Пусть наперед задано любое положительное число t. Тогда в течение интервала времени от начала движения до момента t охотник может бежать по любой траектории; начиная с момента t охотник может двигаться по любой из бесчисленного множества прямолинейных траекторий, удовлетворяющих условиям задачи.)
Наконец, при условии  , человек может сколь угодно близко подбежать к лисе, выбрав соответствующий малый угол φ.
, человек может сколь угодно близко подбежать к лисе, выбрав соответствующий малый угол φ.
Читателю предлагается самому доказать эти утверждения и нарисовать нужные рисунки.
3. Пароход и катер
Перпендикулярно к прямолинейному берегу моря проходит канал. Вдоль берега с постоянной скоростью ![]() плывет пароход. Катер начинает движение по каналу из точки В, когда пароход находится в точке А — у устья канала. С какой постоянной скоростью и должен двигаться катер, чтобы на максимальное сближение с пароходом (до того, как катер вышел в море) потребовалось максимальное время?
плывет пароход. Катер начинает движение по каналу из точки В, когда пароход находится в точке А — у устья канала. С какой постоянной скоростью и должен двигаться катер, чтобы на максимальное сближение с пароходом (до того, как катер вышел в море) потребовалось максимальное время?
(*Несколько лет назад эта задача предлагалась на вступительных экзаменах по математике (письменно) на естественные факультеты Ленинградского университета. Составители вариантов предполагал, что задача будет решаться алгебраически. Решение при этом оказывается громоздким. Попробуйте провести его сами.)
Обозначим скорость катера в системе отсчета, в которой пароход неподвижен, через  :
: 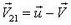 (рис. 3).
(рис. 3).
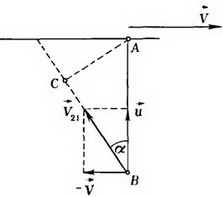
Рис. 3.
В этой системе отсчета траектория катера до максимального сближения есть отрезок ВС: 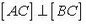 расстояние |АС| — кратчайшее расстояние между судами. Время, за которое катер достигнет точки С,
расстояние |АС| — кратчайшее расстояние между судами. Время, за которое катер достигнет точки С,
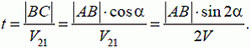
Величина t принимает максимальное значение при 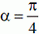 , т. е. когда
, т. е. когда
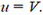
4. Корабли в тумане
Четыре корабля А, Б, В и Г плывут в тумане с постоянными скоростями прямолинейными курсами. Корабли А и Б чуть не столкнулись; назовем это событие «столкновением».
Известно, что произошли следующие столкновения: А и Б, А и В, А и Г, Б и В, Б и Г, причем в одном месте в одно и то же время сталкивалось не больше двух кораблей. Докажите, что если скорости кораблей В и Г различны по величине, то они также сталкиваются.
Рассмотрим перечисленные события с точки зрения наблюдателя, находящегося на корабле А. В этой системе отсчета траектория корабля Б — прямая, проходящая через точку А (сам корабль А в этой системе отсчета неподвижен). Траектория корабля В также есть прямая, проходящая через точку А. Допустим, что траектории кораблей Б и В не совпадают (изобразим траекторию корабля В пунктиром; см. рис. 4).
Рис. 4.
В этом случае в точке А происходит столкновение сразу трех кораблей: А, Б и В (иначе корабли Б и В не столкнутся), что противоречит условию задачи. Следовательно, в нашей системе отсчета траектории кораблей Б и В совпадают, а столкновение Б и В происходит не в точке А, а где-то в другом месте. Точно так же можно убедиться, что траектория корабля Г совпадает с траекториями кораблей Б и В. Поскольку у кораблей В и Г величины скоростей по условию различны, различны и величины их скоростей в выбранной системе отсчета. Таким образом, в этой системе отсчета корабли В и Г движутся по одной прямой с разными скоростями и, следовательно, неизбежно сталкиваются. (*Другой способ решения см. в книге Дж. Литлвуда «Математическая смесь» (М., «Наука», 1965), с. 10.)
5. Осторожный охотник и лиса
Лиса бежит с постоянной скоростью по прямой l. Охотник замечает лису, когда она находится на расстоянии а от него в направлении, составляющем угол α с прямой l (рис. 5, а), и начинает преследование, двигаясь с той же по величине скоростью, что и лиса. Поскольку «тактика» лисы охотнику неизвестна, он бежит все время прямо за лисой. Как близко охотнику удастся подбежать к лисе?
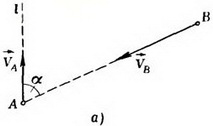
Рис. 5.
(*Эта интересная задача однажды подробно обсуждалась в «Кванте» (1973, № 2, с. 39).)
Рассмотрим события в системе Оху, где лиса неподвижна и находится в начале координат О (ось Оу направлена вдоль лисьей тропы в сторону движения лисы). Скорость охотника в этой системе 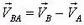 , где
, где 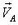 и
и 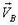 — скорости лисы и охотника в неподвижной системе отсчета. Пусть в некоторый момент времени охотник находится в точке В1 (рис. 5, б).
— скорости лисы и охотника в неподвижной системе отсчета. Пусть в некоторый момент времени охотник находится в точке В1 (рис. 5, б).
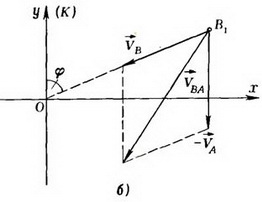
Рис. 5.
Обозначим проекции скорости 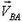 охотника на направления
охотника на направления 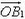 и
и 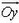 (см. рис. 5, б) через V1 и V2. Если
(см. рис. 5, б) через V1 и V2. Если 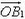 составляет с направлением
составляет с направлением 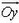 угол φ, то
угол φ, то
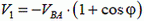
и
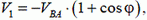
то есть 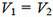 в любой момент времени. Следовательно, в любой момент времени охотник равноудален от начала координат О системы координат Оху и некоторой прямой, параллельной оси Ох. Найдем уравнение этой прямой. В начальный момент времени охотник удален от лисы (т. е. от начала координат) на расстояние а, поэтому искомая прямая отстоит от точки В на расстоянии а (рис. 5, в).
в любой момент времени. Следовательно, в любой момент времени охотник равноудален от начала координат О системы координат Оху и некоторой прямой, параллельной оси Ох. Найдем уравнение этой прямой. В начальный момент времени охотник удален от лисы (т. е. от начала координат) на расстояние а, поэтому искомая прямая отстоит от точки В на расстоянии а (рис. 5, в).
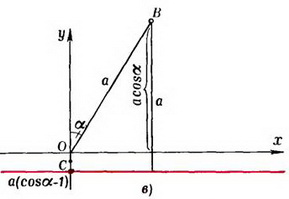
Рис. 5.
Таким образом, уравнение этой прямой в системе координат Оху имеет вид 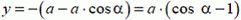 , прямая находится на расстоянии
, прямая находится на расстоянии 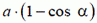 от начала координат. Поэтому ближайшее к лисе положение охотника — это точка С, расположенная на оси Оу на одинаковом расстоянии
от начала координат. Поэтому ближайшее к лисе положение охотника — это точка С, расположенная на оси Оу на одинаковом расстоянии 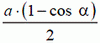 от О и от найденной прямой:
от О и от найденной прямой:
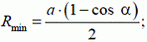
оно достигается, когда охотник находится на прямой l.
6. Грустная история зайца
По прямой с постоянной скоростью ![]() бежит заяц. В тот момент, когда заяц находится в точке А, волк начинает погоню из точки В с координатами (а; α) (рис. 6 а), двигаясь с постоянной по величине скоростью
бежит заяц. В тот момент, когда заяц находится в точке А, волк начинает погоню из точки В с координатами (а; α) (рис. 6 а), двигаясь с постоянной по величине скоростью 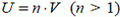 , направленной все время к зайцу. Будет ли заяц пойман, и если да, то когда и где?
, направленной все время к зайцу. Будет ли заяц пойман, и если да, то когда и где?
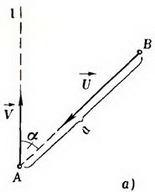
Рис. 6.
Перейдем в систему отсчета, где заяц неподвижен и находится в начале координат О. (Наверное, в этой системе отсчета зайцу очень страшно — ведь он бездействует!). Пусть ось Оу направлена вдоль заячьей тропы в сторону движения зайца. Скорость волка в этой системе ![]() . Докажем прежде всего, что заяц будет пойман.
. Докажем прежде всего, что заяц будет пойман.
Пусть точка В1 есть положение волка в какой-то момент времени и пусть ![]() составляет с осью Оу угол φ (рис. 6 б). Проекция скорости
составляет с осью Оу угол φ (рис. 6 б). Проекция скорости ![]() на направление
на направление ![]() .
.
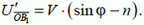 (1)
(1)
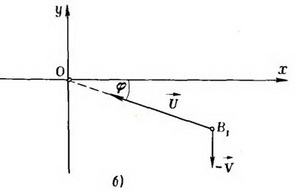
Рис. 6.
По условию n > 1 значит, для любых φ величина 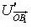 отрицательна, причем
отрицательна, причем 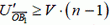 . Поэтому волк обязательно догонит зайца за время, не большее
. Поэтому волк обязательно догонит зайца за время, не большее 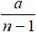 (в начальный момент он находится от зайца на расстоянии а).
(в начальный момент он находится от зайца на расстоянии а).
Найдем теперь время, за которое волк догонит зайца. Для этого запишем проекцию скорости 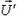 на направление оси Оу выбранной системы координат. Имеем (см. рис. 6 б):
на направление оси Оу выбранной системы координат. Имеем (см. рис. 6 б):
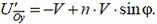 (2)
(2)
Пусть (х; у) — координаты волка в системе Оху. В момент времени Т, когда заяц пойман, 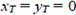 . В начальный момент времени
. В начальный момент времени 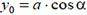 . Таким образом, проекция на ось Оу перемещения волка за время Т, необходимое для поимки зайца, равна
. Таким образом, проекция на ось Оу перемещения волка за время Т, необходимое для поимки зайца, равна 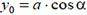 . Поэтому среднее значение проекции скорости волка на ось Оу за время Т
. Поэтому среднее значение проекции скорости волка на ось Оу за время Т
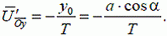
Найдем теперь из (1) и (2) соотношение между 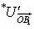 и
и 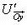 . Имеем:
. Имеем:
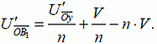
Поскольку слагаемые 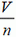 и
и 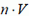 от времени не зависят, такое же соотношение справедливо и для средних значений рассматриваемых проекций, то есть
от времени не зависят, такое же соотношение справедливо и для средних значений рассматриваемых проекций, то есть
 (3)
(3)
С другой стороны,
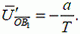 (4)
(4)
Из (3) и (4) находим искомое время поимки:
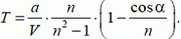 (5)
(5)
Проверим этот ответ для очевидных частных случаев.
1) α = 0: волк бежит навстречу зайцу. В этом случае величина относительной скорости движения волка равна V·(n + 1), так что он догонит зайца за время
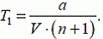
Этот же результат получается из (5) при подстановке α = 0.
2) α = π: волк бежит за зайцем. При этом величина его относительной скорости равна V·(n – 1) (n > 1), и он догоняет зайца за время
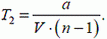
Подставляя α = π в выражение (5), получаем тот же ответ.
За время Т заяц пробегает расстояние
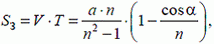
так что волк ловит зайца в точке на прямой l, отстоящей от точки А на этом расстоянии SЗ.
Задачи
1. На луг перпендикулярно к опушке леса выходит прямолинейное шоссе. Из леса со скоростью ![]() выезжает автобус. Из какой части луга имеет смысл бежать, чтобы догнать автобус, если вы можете двигаться со скоростью
выезжает автобус. Из какой части луга имеет смысл бежать, чтобы догнать автобус, если вы можете двигаться со скоростью ![]() (U < V).
(U < V).
2. Докажите, что все четыре корабля А, Б, В и Г из задачи 5 в любой момент времени находятся на одной прямой.
3. В каждой вершине правильного n-угольника находится по собаке. По команде все собаки одновременно начинают движение, причем каждая преследует свою ближайшую по часовой стрелке соседку. Какое время проходит до встречи собак и какое расстояние пробегает каждая из них, если они бегут со скоростью V?
4. Квадратный огород окружен забором. В вершине А забора сидит собака-сторож. В противоположной вершине В — дырка, достаточная для зайцев, но слишком узкая для собаки. Пробравшийся в огород воришка-заяц, заметив собаку, бежит к дырке по прямой со скоростью V; собака преследует его со скоростью n·V, n > 1, причем всегда бежит прямо за зайцем. Определите (приблизительно), в какой части огорода заяц может чувствовать себя в безопасности.
5. Несколько собак окружили зайца. Скорости собак не превышают скорости зайца. Все собаки зайцу видны. Может ли заяц вырваться из окружения, и если да, то как, если собаки при преследовании бегут так, что скорость каждой из них всегда направлена к той точке, где в данный момент находится заяц?
| Выложил | alsak |
| Опубликовано | 21.05.09 |
| Просмотров | 15963 |
| Рубрика | Решение задач |
| Тема | Кинематика |