Беляев С.А. Кинематика и связи // Квант
Беляев С.А. Кинематика и связи // Квант. — 1971. — № 2. — С. 44-46.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Кинематика часто рассматривает движение абсолютно твердых тел, то есть тел, расстояния между любыми двумя точками которых остаются постоянными. При этом существуют методы, значительно упрощающие решение кинематических задач. С одним из них мы сейчас познакомимся.
Пусть тела при движении соприкасаются, и скольжение между ними отсутствует. Тогда скорости обоих тел в точке соприкосновения полностью совпадают (рис. 1).
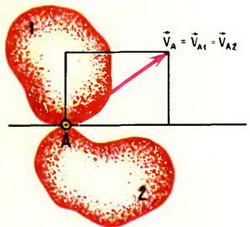
Рис. 1
Если же между телами есть проскальзывание, то совпадают лишь проекции скоростей на перпендикуляр к касательной в точке соприкосновения. При этом достаточно, чтобы касательная существовала хотя бы для одной из скользящих поверхностей (рис. 2).
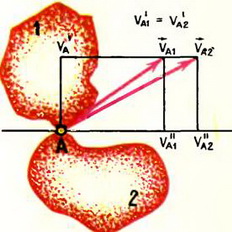
Рис. 2.
Рассмотрим несколько примеров.
1. Стержень ОА вращается по часовой стрелке с угловой скоростью ω, приводя в движение кирпич ABCD с боковой стороной а (рис. 3). Найти зависимость скорости кирпича υ от угла α.
Решение. Стержень и кирпич соприкасаются в точке А. Следовательно, скорости кирпича и стержня в этой точке в направлении MN 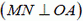 совпадают. Таким образом,
совпадают. Таким образом,
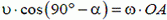
или
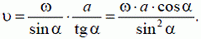
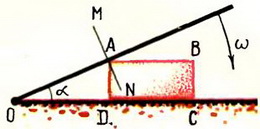
Рис. 3.
2. Источник света S находится на расстоянии l от экрана MN (рис. 4). В начальный момент времени плоский предмет высоты h начинает равномерно двигаться со скоростью υ от источника к экрану. Найти зависимость скорости движения края тени по экрану от времени.
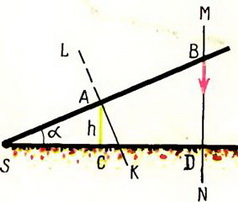
Рис. 4.
Решение. В данной задаче в роли стержня выступает луч SB. В точке А луч «соприкасается» с предметом, а в точке В с экраном, образуя границу тени. Составим два уравнения, связывающих проекции скоростей в точках А и В: 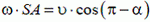 — проекция на LК,
— проекция на LК, ![]() — проекция на MN. Здесь ω — угловая скорость вращения луча. Разделив второе равенство на первое и учитывая, что
— проекция на MN. Здесь ω — угловая скорость вращения луча. Разделив второе равенство на первое и учитывая, что
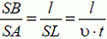 и
и 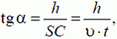
получим
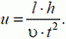
Пусть теперь стержень АВ заданной длины l (рис. 5) движется произвольно. Скорости 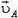 и
и 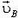 его концов могут быть различны, но, так как длина стержня не меняется, проекции этих скоростей
его концов могут быть различны, но, так как длина стержня не меняется, проекции этих скоростей 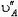 и
и 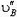 должны быть равны:
должны быть равны: 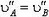 . Проекции скоростей
. Проекции скоростей 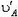 и
и 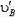 определяют круговое движение стержня с угловой скоростью
определяют круговое движение стержня с угловой скоростью 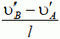 (проверьте это самостоятельно).
(проверьте это самостоятельно).
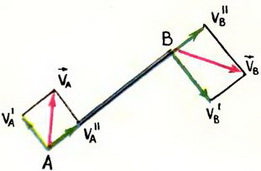
Рис. 5.
Решим две задачи.
3. Стержень АВ опирается своими концами о стороны тупого угла β (рис. 6). Верхний конец стержня тянут со скоростью υ вдоль стороны АО. Найти зависимость скорости u точки В от угла α.
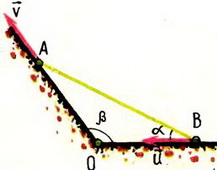
Рис. 6.
Решение. Так как длина стержня АВ неизменна, проекции скоростей его концов на направление стержня одинаковы:

или
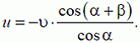
Рассмотрим случай, когда длина стержня изменяется во время движения («стержнем» может служить, например, отрезок, соединяющий две заданные точки, расстояние между которыми меняется). Тогда соотношение, связывающее проекции скоростей концов стержня, принимает вид
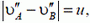
где u — скорость изменения длины стержня. (Модуль здесь нужен, так как неизвестно, какая из скоростей больше.)
4. Лодку с крутого берега тянут за веревку с постоянной скоростью υ. Найти зависимость скорости лодки u от угла α.
Решение. В данном случае нас интересует часть веревки АВ. Скорость ее сокращения равна υ. Векторы скоростей концов, веревки А и В показаны на рисунке 7.
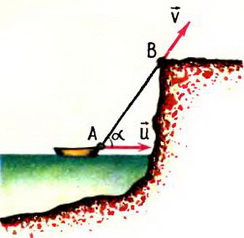
Рис. 7.
Согласно утверждению, приведенному выше, имеем
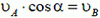
или так как 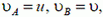 то
то
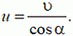
Попробуйте самостоятельно решить подобные задачи.
1. Стержень ОА вращается по часовой стрелке с угловой скоростью ω, приводя в движение цилиндр радиуса r (рис. 8). Скольжения между цилиндром и плоскостью нет. Найти зависимость скорости цилиндра υ от угла α.
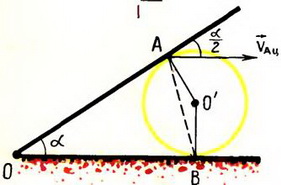
Рис. 8.
2. Кривошип АО длины r (рис. 9) вращается с угловой скоростью ω, длина шатуна АВ равна l. Найти скорость υ точки В шатуна, если 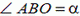 .
.
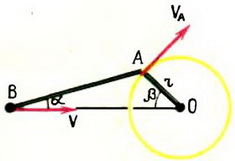
Рис. 9.
3. Шарик, предварительно раскрутив вокруг оси, кладут на горизонтальную поверхность. Коэффициент трения шарика о поверхность отличен от нуля. Под действием силы трения шарик изменяет свое первоначальное вращательное движение и начинает каким-то образом двигаться по поверхности. Описать, как будет происходить это движение.
Ответы
1. (*На рисунке к этой задаче вектор скорости υAц должен быть направлен под углом α/2 к стержню.)
В точке А проекции скоростей цилиндра υAц и стержня υAС на направление АО´ 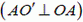 совпадают. Значение υAС равно
совпадают. Значение υAС равно 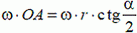 . Заметим, что мгновенная ось вращения цилиндра проходит через точку В. Поэтому υAц направлена перпендикулярно АВ и равна ω·AB, где ω — угловая скорость вращения цилиндра. Поскольку
. Заметим, что мгновенная ось вращения цилиндра проходит через точку В. Поэтому υAц направлена перпендикулярно АВ и равна ω·AB, где ω — угловая скорость вращения цилиндра. Поскольку
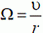 и
и 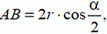
получим
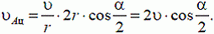
Из условия равенства проекции имеем
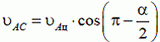
или
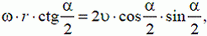
Откуда
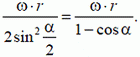
2. Поскольку длина АВ неизменна, проектируя скорости концов шатуна на направление АВ, получим 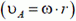 :
:
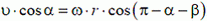
или
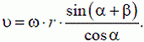
Воспользовавшись теоремой синусов
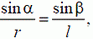
можно найти
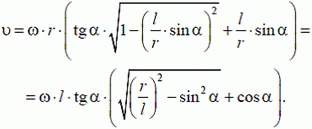
| Выложил | alsak |
| Опубликовано | 24.05.09 |
| Просмотров | 13701 |
| Рубрика | Решение задач |
| Тема | Кинематика |