Башмаков М.И. Равномерное движение // Квант
Башмаков М.И. Равномерное движение // Квант. — 1983. — № 3. — С. 26-30.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Мы здесь рассматриваем прямолинейное равномерное движение, то есть движение по фиксированной прямой с постоянной скоростью. Выбрав направление на этой прямой, можно записать уравнение движения в виде
 (1)
(1)
где t — время движения, s и υ — проекции векторов перемещения и скорости на выбранную ось. Тогда s и υ могут принимать как положительные, так и отрицательные значения.
Средняя скорость
Формулу (1) часто записывают в виде  . Соотношение
. Соотношение  имеет смысл и для неравномерного движения (движения с переменной скоростью), но в этом случае υ является по определению средней скоростью движения.
имеет смысл и для неравномерного движения (движения с переменной скоростью), но в этом случае υ является по определению средней скоростью движения.
В качестве разминки, постарайтесь, не составляя уравнений, ответить на следующие вопросы:
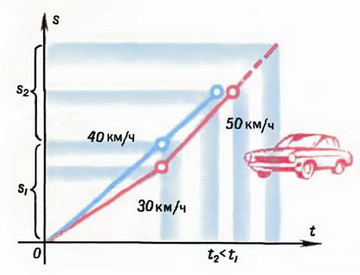
1. Одна машина шла первую половину пути со скоростью 30 км/ч, а вторую — со скоростью 50 км/ч. Вторая машина шла весь путь со скоростью 40 км/ч. Какая из машин затратила на всю дорогу меньше времени? (При s1 = s2 вторая машина затратила меньше времени, см. рис. 1, а)
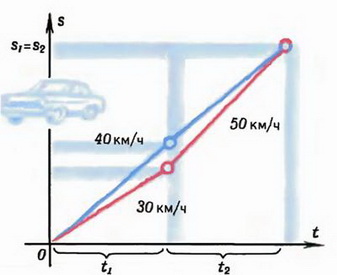
2. Одна машина первую половину времени движения шла со скоростью 30 км/ч, а вторую — со скоростью 50 км/ч. Вторая машина двигалась столько же времени, сколько и первая, причем ее скорость была все время 40 км/ч. Какая из машин прошла большее расстояние? (При t1 = t2 обе машины прошли одинаковое расстояние, см. рис. 1, б)
а
б
Рис. 1.
Возможные ошибки при ответах на вопросы о равномерном движении связаны с тем, что мы иногда путаем характер зависимости между двумя из величин s, υ и t при фиксированной третьей.
При фиксированном перемещении зависимость между временем и скоростью — обратно пропорциональная. При этом, если перемещение 2s > 0 состоит из двух одинаковых участков s, которые проходятся с постоянными (но разными) скоростями, первый за время t1, второй, за время t2, то средняя скорость  меньше среднего арифметического скоростей на каждом из участков, равного
меньше среднего арифметического скоростей на каждом из участков, равного

Действительно, разность

очевидно, положительна, то есть  .
.
Так, в задаче 1 средняя скорость первой машины меньше, чем (30 + 50)/2 км/ч = 40 км/ч, значит вторая машина (шедшая со скоростью 40 км/ч) приедет быстрее.
При фиксированном времени движения зависимость между перемещением и скоростью — прямо пропорциональная. Поэтому если в течение двух одинаковых отрезков времени t происходит равномерное движение с разными скоростями υ1 и υ2, то средняя скорость υ на всем пути будет равна среднему арифметическому скоростей на отдельных участках. Действительно,

Так, в задаче 2 средняя скорость первой машины равна скорости второй ((50+30)/2 = 40) и поэтому они за одинаковое время совершают одинаковое перемещение.
Полезно изображать движение графически, рассматривая перемещение как функцию от времени: s = s(t). Для первых двух задач это сделано на рисунке 1, а, б.
В заключении этого раздела самостоятельно решите следующую задачу.
3. Пусть si, ti — положительные числа (i = 1, 2,..., п). Докажите, что дробь

лежит между наименьшей и наибольшей из дробей

Сформулируйте результат в терминах средних скоростей.
Относительное движение.
К совсем простым задачам, часто неверно решаемым, относится задача
4. Когда катер затрачивает на движение туда и обратно на данное расстояние меньше времени — при движении по реке (с постоянной скоростью течения) или в стоячей воде?
Кажется очевидным, что время будет одинаковым — ведь при движении по реке туда и обратно скорость течения в одну сторону прибавляется к скорости катера, а в другую — вычитается, так что изменения в скорости компенсируют друг друга. Однако это не так. На самом деле катер обернется быстрее в стоячей воде!
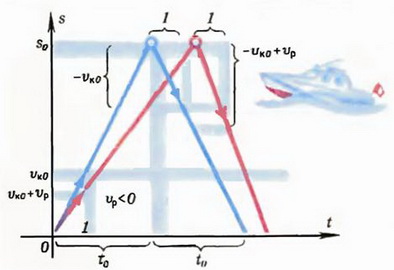
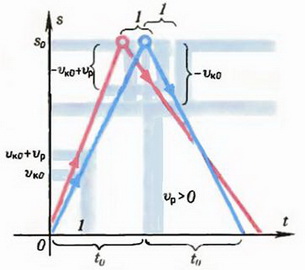
Графики движения катера показаны на рисунке 2.
а
б
Рис. 2.
Даже если вы правильно угадали ответ, очень советую аккуратно обосновать его; кроме формулы (1), вам потребуется обычная формула сложения скоростей:

утверждающая, что скорость υк катера в реке равна сумме его скорости в стоячей воде υк0 и скорости реки υр.
В задаче с катером мы столкнулись с наложением двух равномерных движений — движения катера и движения воды в реке. С такой ситуацией связано много интересных и неожиданных задач.
Попробуйте без вычислений решить такую задачу.
5. По движущемуся вверх эскалатору в направлении движения идет человек и считает пройденные ступени. Скорость человека относительно неподвижного эскалатора равна υ. Как выглядит график зависимости числа s пройденных им ступеней от скорости υ?
Прежде чем рисовать график, ответьте для себя на вопрос: возрастает или убывает функция с ростом скорости υ? Грубый эскиз графика изображен на рисунке 3.

Рис. 3.
Давайте изучим ситуацию более подробно. Обозначим общее число ступеней (неподвижного) эскалатора через s0, скорость движения эскалатора через υэ, скорость подъема человека через υ, число ступеней, пройденных человеком, через s. Эти величины связаны соотношением

(мы приравняли время подъема человека и время подъема эскалатора).
Отсюда находим

Начертим график функции
 (2)
(2)
считая, что υ может принимать любые (в том числе и отрицательные) значения. График изображен на рисунке 4.

Рис. 4.
Глядя на график (и вспоминая условия задачи), ответьте на следующие вопросы:
а) Что происходит с s при неограниченно возрастающем υ?
б) Какой смысл имеют отрицательные значения υ?
в) Как можно объяснить, что s неограниченно возрастает, если υ приближается к (–υэ)? Представьте себе, что вы встали на первую ступеньку движущегося вверх эскалатора и начали спускаться вниз с той же скоростью, что и сам эскалатор. Далеко ли вы уйдете? А сколько ступеней вы можете пройти?
г) Как изменится график функции (2), если одновременно заменить υ на k·υ и υэ на k·υэ?
Ответ на последний вопрос — график не изменяется — означает, что число пройденных ступенек зависит только от отношения скоростей человека и эскалатора.
В заключении этого раздела предлагаем еще две задачи.
6. Человек, поднимаясь по эскалатору, насчитал 100 ступеней, а двигаясь с вдвое большей скоростью, насчитал 120 ступеней. Сколько ступеней на неподвижном эскалаторе?
7. Человека, идущего вдоль трамвайных путей, каждые 7 минут обгоняет трамвай, а каждые 5 минут трамвай проходит навстречу. Как часто ходят трамваи?
Кусочно-линейное движение
Простота формулы  обусловлена тем, что за начало отсчета выбрана точка на прямой, в которой находится движущееся тело в момент времени t = 0. Если сдвинуть начало отсчета на s0 (влево или вправо, в зависимости от знака), уравнение равномерного движения примет вид
обусловлена тем, что за начало отсчета выбрана точка на прямой, в которой находится движущееся тело в момент времени t = 0. Если сдвинуть начало отсчета на s0 (влево или вправо, в зависимости от знака), уравнение равномерного движения примет вид
 (3)
(3)
На графике (рис. 5) движение изображается прямой (пересекающей ось s в точке s0) наклон которой зависит от скорости υ. Положительный наклон (острый угол) соответствует положительным скоростям (то есть движению в положительном направлении оси s), отрицательный — движению в обратном направлении.
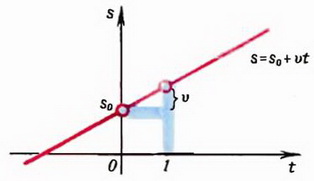
Рис. 5.
Формула (3) полезна в тех случаях, когда мы на едином графике изображаем кусочно-линейное движение, то есть движение, которое является равномерным (но с разными скоростями) на соседних отрезках времени. На графике такое движение изображается в виде ломанной линии, каждое звено которой задается функцией вида (3) на соответствующем отрезке времени (рис. 6, а). Если же изобразить скорость такого движения как функцию времени  , то получим кусочно-постоянную (ступенчатую) функцию (рис. 6, б). Связь между графиками кусочно-постоянной функции скорости и кусочно-линейной функции пути хорошо видна на рисунке 6.
, то получим кусочно-постоянную (ступенчатую) функцию (рис. 6, б). Связь между графиками кусочно-постоянной функции скорости и кусочно-линейной функции пути хорошо видна на рисунке 6.

Рис. 6.
Мы теперь воспользуемся этими соображениями, чтобы решить более трудную (олимпиадную) задачу, на первый взгляд не имеющую отношения к равномерному движению.
8. По кругу выписано 10 чисел, сумма которых равна нулю. Мы начинаем с одного из них, например, а1, и последовательно складываем их по кругу (скажем, по часовой стрелке). Получим суммы а1, а1 + а2, а1 + а2 + а3,..., а1 + а2 + … + а10 = 0. Докажите, что можно так выбрать начальное число, что все эти суммы будут неотрицательны.
Для решения представим себе, что а1, а2, ..., а10 — скорости движения на десяти равных отрезках времени, которые примем за единицу.
Считая, что в начальный момент путь равен нулю, получим, что путь s через единицу времени будет равен а1, через две единицы — а1 + а2, и т. д. График такой функции изобразится ломаной, начинающейся и кончающейся на оси t, так как по условию а1 + а2 + +… + а10 = 0 (рис. 7, а). Можно считать, что движение повторяется периодически — через десять единиц времени скорость снова равна а1 и т. д. График движения представится в виде периодически повторяющейся 10-звенной ломаной (рис. 7, а). Начало отсчета в другой точке означает перенос начала координат в одну из вершин ломаной. Что означает неотрицательность сумм? Она означает, что все вершины ломаной лежат выше оси времени (или на ней). Сначала мы выбрали начальную точку произвольно (рис. 7, а). Теперь ясно, что если перенести начало координат в вершину ломаной, для которой значение наименьшее, и начать отсчет от этой точки, то последовательные суммы будут неотрицательны (рис. 7, б).
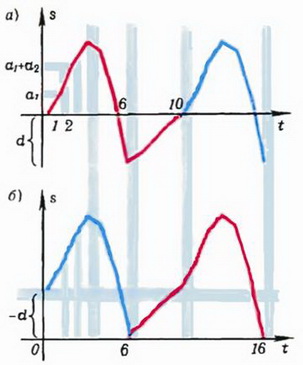
Рис. 7.
9. На кольцевой дороге расположено 10 пунктов, в каждом из которых шофер может получить 20 литров бензина. На все кольцо ему нужно все 200 литров. Доказать, что он может так выбрать начальный пункт движения, что забирая по пути бензин, он сможет проехать все кольцо. Ограничений на объем бензобака нет.
10*. Несколько человек наблюдало за неравномерно ползущей улиткой. Каждый наблюдатель следил за улиткой одну минуту и отметил, что средняя скорость улитки на наблюдаемом участке равна 1 см/мин. Улитка ползла 6 минут и при этом в каждый момент времени за ней кто-нибудь наблюдал. Какое наименьшее и какое наибольшее расстояние могла проползти улитка?
Указание. Легко сообразить, что если улитка ползет равномерно, то за 6 минут она проползет 6 см. Попробуйте сначала заставить двигаться улитку и так организовать наблюдение за ней, чтобы она проползла при соблюдении условий задачи больше 6 см и меньше 6 см. «Сдвинувшись» с 6 см, вам проще будет получить правильный ответ.
| Выложил | alsak |
| Опубликовано | 24.05.09 |
| Просмотров | 12560 |
| Рубрика | Решение задач |
| Тема | Кинематика |