Гурский И.П. Кинематика прямолинейного движения материальной точки //Квант
Гурский И.П. Кинематика прямолинейного движения материальной точки //Квант. — 1973. — № 11. — С. 57-60.
По специальной договоренности с редколлегией и редакцией журнала «Квант».
Равномерное прямолинейное движение
Равномерным прямолинейным движением называется движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения. Уравнение такого движения в векторной форме записывается так:
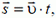
где 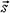 — перемещение,
— перемещение, 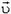 — скорость движения, t — время.
— скорость движения, t — время.
Движение материальной точки всегда рассматривается относительно какого-либо тела, которое в данной задаче принимается за неподвижное и называется телом отсчета. С ним связывается система координат; вместе с телом отсчета они образуют систему отсчета. Для прямолинейного движения достаточно выбрать одну ось координат, например ОХ. Тогда положение точки будет определяться его координатой х. Уравнение равномерного движения в скалярной форме будет выглядеть так:
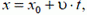
где x0 — координата точки в момент времени t = 0.
Правильный выбор системы отсчета часто существенно облегчает решение задачи. Рассмотрим несколько конкретных задач.
Задача 1. Пассажир, сидящий у окна поезда, идущего со скоростью υ1 = 72 км/ч, видит встречный поезд, идущий со скоростью υ2 = 31,4 км/ч, в течение 10 секунд. Определить длину встречного поезда.
За тело отсчета примем пассажира, а ось координат направим по направлению скорости встречного поезда. Величины скоростей υ1 и υ2 заданы относительно некоторой неподвижной системы отсчета, например земли. По отношению же к пассажиру, движущемуся со скоростью υ1, встречный поезд имеет так называемую относительную скорость υ2отн, которая равна
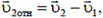
или в скалярной форме
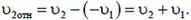
Тогда искомая длина встречного поезда l равна
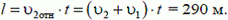
Задача 2. Рыбак плывет на лодке вверх по реке; проезжая под мостом, он уронил в воду соломенную шляпу. Через полчаса он это обнаружил и, повернув назад, догнал шляпу в 5 км ниже моста. Какова скорость течения реки, если рыбак, двигаясь вверх и вниз по реке, греб одинаково?
Свяжем систему отсчета с водой в реке, то есть со шляпой. Рыбак удаляется от шляпы и приближается к ней с одной и той же скоростью, следовательно, он догонит ее через полчаса после того, как обнаружил потерю, или через час после падения шляпы в воду. За это время шляпа относительно земли проплыла 5 км. Значит, скорость течения реки равна 5 км/ч.
Равнопеременное прямолинейное движение
Если скорость материальной точки не постоянна, но в любые равные промежутки времени она изменяется на одну и ту же величину, то в этом случае говорят о равнопеременном движении. Движение называют равноускоренным, если скорость увеличивается, и равнозамедленным, если скорость уменьшается.
Для решения задач на эту тему достаточно знать уравнения для скорости и перемещения. В скалярной форме они записываются так:
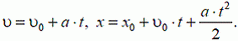
Здесь υ0 — начальная скорость точки, х0 — начальная координата, а — ускорение, υ и х — соответственно скорость и координата точки в момент времени t. Величины υ0, a, υ и х будем считать положительными, когда их направление совпадает с положительным направлением выбранной оси координат ОХ, отрицательными — в противном случае.
Начинать решение задачи полезно с краткой записи ее условия, по возможности полностью переводя задачу на язык условных обозначений. При этом надо следить за тем, чтобы единицы измерения всех величин были даны в одной и той же системе единиц. Все расчеты лучше проводить в общем виде, то есть в буквенных обозначениях, а численные значения подставлять в окончательный результат.
Решим следующие задачи.
Задача 3. Два велосипедиста едут друг другу навстречу: один из них, имея скорость 5,4 км/ч, спускается с горы с ускорением 0,2 м/с2; другой, имея скорость 18 км/ч, поднимается в гору с ускорением — 20 см/с2. Через сколько времени они встретятся?
Пусть начало координат совпадает с начальным положением первого велосипедиста, а положительное направление оси координат — с направлением его начальной скорости. Тогда краткая запись условия задачи будет выглядеть так:
υ01 = 5,4 км/ч = 1,5 м/с
υ02 = –18 км/ч = –5 м/с
a1 = 0,2 м/с2
a2 = 20 см/с2 = 0,20 м/с2
x02 = 195 м.
t = ?
Запишем уравнения движения для каждого велосипедиста:
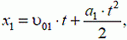 (1)
(1)
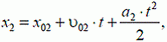 (2)
(2)
причем а1 = а2 по условию. В момент встречи
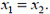 (3)
(3)
Решая совместно уравнения (1) — (3), получим
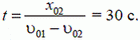
На этом можно было бы закончить решение, но в данном случае следует убедиться в том, что полученный ответ имеет физический смысл. Для этого найдем скорость второго велосипедиста через 30 с после начала движения:
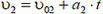 = –5 м/с + 0,2 м/с2 • 30 с = 1 м/с.
= –5 м/с + 0,2 м/с2 • 30 с = 1 м/с.
Оказывается, что второй велосипедист к этому времени будет скатываться с горы, а не подниматься в гору. Очевидно, что данная задача составлена некорректно.
Задача 4. Аэростат поднимается с земли вертикально вверх с ускорением 2,45 м/с2. Через 8 секунд от начала движения из его гондолы выпадает предмет. Через сколько времени и с какой скоростью этот предмет упадет на землю? Сопротивлением воздуха пренебречь.
Так как сначала предмет движется вместе с аэростатом, то через t1 = 8 с он поднимется на некоторую высоту h1 и будет иметь скорость υ1 причем
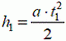 и
и 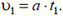
Дальнейшее движение предмета можно описать по-разному.
Часто задачи такого типа решаются в два этапа. Сначала рассматривается замедленное движение предмета вверх до наибольшей высоты, затем — свободное падение на землю. Задача, однако, решается проще, если считать, что предмет одновременно участвует в двух независимых друг от друга движениях: он равномерно со скоростью υ1 поднимается вверх и свободно падает. Свяжем систему отсчета с землей, а ось координат направим вверх. Тогда уравнение движения предмета с высоты h1 до земли запишется так:
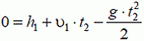
(t2 — время движения предмета). Подставляя в это уравнение выражения для h1 и υ1, получим
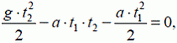
откуда t2 ≈ 6,5 с.
Задача 5. Тело брошено вертикально вверх с некоторой начальной скоростью. Когда оно достигло высшей точки подъема на высоте Н = 100 м от земли, из того же начального пункта и с той же начальной скоростью брошено второе тело. На какой высоте они встретятся? Какие они будут иметь скорости в момент встречи? С какой начальной скоростью были брошены тела? Сопротивлением воздуха пренебречь.
Рассмотрим сначала некоторые особенности движения тела, брошенного вертикально вверх. Это сложное движение является суммой двух простых — равномерного движения и свободного падения. Причем каждое движение происходит независимо от другого и от того, поднимается или опускается тело. Поэтому можно сказать, что время прохождения телом одного и того же участка пути вверх и вниз одно и то же и что скорости тела на некоторой высоте при движении вверх или вниз одинаковы по величине.
Покажем, например, что время подъема тела до максимальной высоты равно времени падения до начального положения и что конечная скорость по величине равна начальной скорости. Пусть начальная скорость тела равна υ0. Запишем уравнения для скорости и координаты (начало координат свяжем с точкой бросания и ось координат направим вверх):
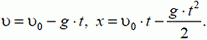
В точке максимального подъема υ = 0, поэтому
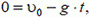
откуда
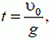
и
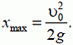
Теперь тело начинает свободно падать. Обозначим время падения t', а конечную скорость υ' и запишем уравнения для свободного падения
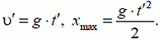
Отсюда
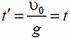
и
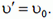
Теперь вернемся к нашей конкретной задаче. Согласно сказанному выше, время подъема второго тела до высоты h (рис. 1), равное времени падения первого тела с высоты H — h, составляет половину времени свободного падения первого тела с высоты Н до земли, то есть
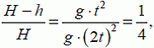
откуда
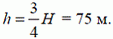
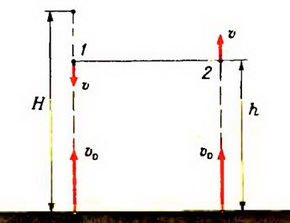
Рис. 1.
Скорости тел в момент встречи одинаковы по величине и равны
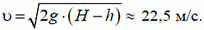
Начальная скорость 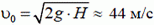 .
.
В заключение рассмотрим задачу на построение графиков.
Задача 6. Дан график зависимости скорости движения тела от времени (рис. 2, а). Построить графики ускорения, перемещения и пути.
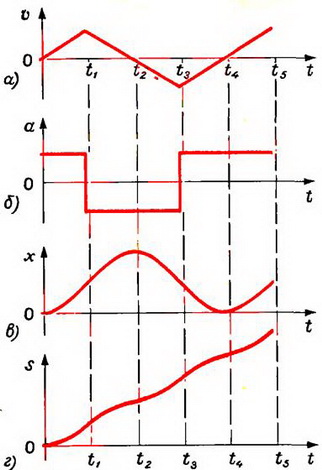
Рис. 2.
Прежде всего, посмотрим, как движется тело в различные моменты времени. Из графика скорости видно, что на первом этапе (от 0 до t1) тело движется равноускоренно; на втором (от t1 до t2) — равнозамедленно; на третьем (от t2 до t3) — равноускоренно, но в обратном направлении; на четвертом (от t3 до t4) — равнозамедленно; на пятом (от t4 до t5) — равноускоренно в первоначальном направлении и т. д. Графики зависимости ускорения, перемещения и пути от времени показаны на рисунках 2, б, в и г соответственно.
Упражнения
1. По двум параллельным путям в одном направлении идут два поезда: пассажирский — длиной 200 м со скоростью 72 км/ч и товарный — длиной 400 м со скоростью 45 км/ч. Сколько времени пассажирский поезд будет обгонять товарный?
2. Замыкающий колонны войск, растянувшейся на 2,5 км и идущей со скоростью 5 км/ч, послал мотоциклиста с извещением командиру, находящемуся во главе колонны. Командир принимал извещение и писал ответ, стоя на обочине дороги, в. течение трех минут. Определить среднюю скорость мотоциклиста, если он вернулся к замыкающему через 9 мин 27 с.
3. Два велосипедиста едут навстречу друг другу: один из них, имея скорость 7,2 км/ч, спускается с горы с ускорением 0,30 м/с2; другой, имея скорость 36 км/ч, поднимается с ускорением —0,20 м/с2. Каково было расстояние между велосипедистами в начальный момент, если они встретились через 0,5 минуты? При какой наибольшей длине горы задача имеет решение?
4. С некоторой высоты падает тело. Через 2 с с той же высоты падает второе тело. Через сколько секунд после начала падения первого тела удвоится расстояние, разделяющее тела до начала падения второго тела? Сопротивлением воздуха пренебречь.
5. Вертолет поднимается вверх со скоростью 10 м/с. На высоте 100 м из него выбрасывается вверх предмет со скоростью 2 м/с относительно вертолета. Найти наибольшую высоту, которой достигнет предмет, а также через сколько времени и с какой скоростью предмет упадет на землю.
6. Тело бросают вверх со скоростью 20 м/с. Какова высота точки, которую тело проходит дважды с промежутком 3 с? Сопротивлением воздуха пренебречь.
7. Дан график зависимости ускорения от времени (рис. 3). Построить график зависимости величины перемещения от скорости.
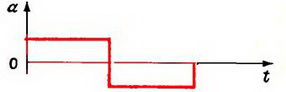
Рис. 3.
Ответы
1. t = 80 c.
2. υср = 12,5 м/c.
3. l0 = 405 м; lmax = 725 м.
4. t = 3 c.
5. Hmax = 107,2 м ; t≈ 5,8 c; u» 46 м/с.
6. h ≈ 8,8 м.
7. См. рисунок 4.
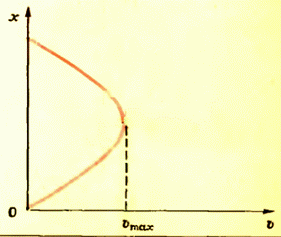
Рис. 4.
| Выложил | alsak |
| Опубликовано | 01.06.09 |
| Просмотров | 33208 |
| Рубрика | Решение задач |
| Тема | Кинематика |