Коржов Н.И. Задача о веревке на блоке
Коржов Н.И.Задача о веревке на блоке // Фiзiка: праблемы выкладання. – 2003. – № 2. – С. 110-116.
Рассмотрим широко известную задачу (см. [1]-[5]), условие которой сформулируем следующим образом.
Однородная гладкая веревка массой m и длиной L переброшена через блок. В начальный момент веревка висит симметрично и покоится, а затем в результате незначительного толчка начинает двигаться по блоку. Какова скорость υ конца веревки в тот момент, когда с одной стороны блока свешивается большая часть веревки длиной x? Чему равно ускорение a конца веревки в этот момент? С какой силой F веревка давит на блок в этот момент? Чему равны силы натяжения веревки Tt и T2 в точках 1 и 2 (рис. 1)? Массой блока пренебречь, радиус блока считать малым, веревка нерастяжима.

Рис. 1
Приступая к решению задачи, допустим, что веревка натянута в каждом своем сечении, что важно для дальнейших рассуждений. В частности, в этом случае модули линейных скоростей всех элементов веревки равны, что позволяет легко вычислять кинетическую энергию веревки. Выберем нулевой уровень потенциальной энергии на уровне оси блока. Тогда в начальный момент потенциальная энергия веревки
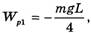
так как центр масс ниже нулевого уровня на L/4. В момент, когда с одной стороны свешивается часть веревки длиной xи массой  (ее центр масс ниже оси блока на x/2), а с другой — часть веревки длиной
(ее центр масс ниже оси блока на x/2), а с другой — часть веревки длиной  и массой
и массой  (ее центр масс ниже оси блока на
(ее центр масс ниже оси блока на 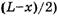 , потенциальная энергия всей веревки
, потенциальная энергия всей веревки
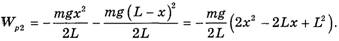
Тогда из закона сохранения механической энергии 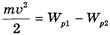 легко найти скорость конца веревки υ:
легко найти скорость конца веревки υ:
 (1)
(1)
Перейдем к нахождению ускорения конца веревки. Поскольку зависимость для скорости известна, оптимальным способом будет нахождение ускорения в соответствии с определением
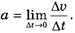
Из соотношения (1) найдем
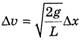
и, учитывая, что по определению

окончательно имеем:
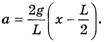 (2)
(2)
Для определения сил натяжения веревки в точках 1 и 2 в литературе [4] (задача 8.20), [6] для левого и правого концов веревки составляется система уравнений, аналогичная стандартной системе уравнений для движения грузов массами m1и m2,связанных невесомой нерастяжимой нитью, перекинутой через блок (рис. 2):
 (*)
(*)
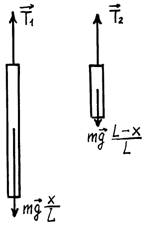
Рис. 2
Из этой системы следует, что
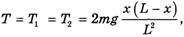 (3)
(3)
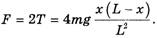 (4)
(4)
Кстати, формула ускорения, получаемая из системы (*), имеет вид (2).) Однако, если по формуле (4) найти ответ к задаче 2.4.13 из [5] (при 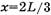 ), то получим
), то получим 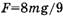 , хотя в книге ответ другой:
, хотя в книге ответ другой:  . В чем же дело? И какой ответ правильный? Оказывается, второй, а значит, формулы (3) и (4) неверны. В [6] сделана попытка объяснить это различие тем, что «небольшой блок может сыграть дурную шутку: ведь часть веревки, которая находится на блоке, обладает центростремительным ускорением и таким образом «съедает» часть силы давления». Далее находится эта часть
. В чем же дело? И какой ответ правильный? Оказывается, второй, а значит, формулы (3) и (4) неверны. В [6] сделана попытка объяснить это различие тем, что «небольшой блок может сыграть дурную шутку: ведь часть веревки, которая находится на блоке, обладает центростремительным ускорением и таким образом «съедает» часть силы давления». Далее находится эта часть 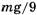 . Такой подход представляется формальным и недостаточно обоснованным, ибо не позволяет выявить истинную причину правильности второго ответа. К тому же формула (3) остается даже при таком подходе, а она неверна, что мы и покажем ниже.
. Такой подход представляется формальным и недостаточно обоснованным, ибо не позволяет выявить истинную причину правильности второго ответа. К тому же формула (3) остается даже при таком подходе, а она неверна, что мы и покажем ниже.
Попробуем корректно найти силы, о которых идет речь в задаче. Главный источник ошибки при выводе формул (3) и (4) — игнорирование того факта, что второй закон Ньютона в форме

применим только к простейшей модели — материальной точке (или поступательно движущемуся абсолютно твердому телу). Веревка же в описанной ситуации ею не является, она даже поступательно не движется. Более того, в отличие от аналогичной ситуации с грузами на невесомой веревке, массы левого и правого концов веревки все время изменяются. В этой ситуации необходимо применять закон изменения импульса системы точек в форме
 (5)
(5)
где 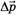 — изменение суммарного импульса системы точек за время Δt, а
— изменение суммарного импульса системы точек за время Δt, а 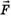 — векторная сумма внешних сил, действующих на тела системы.
— векторная сумма внешних сил, действующих на тела системы.
Рассмотрим два возможных варианта дальнейшего решения задачи. Поскольку блок мал, массой части веревки, прилегающей к блоку, пренебрегаем.
Решение 1. Формулу (5) будем применять для правого и левого концов веревки отдельно, что очень удобно с точки зрения равенства скоростей  и ускорений
и ускорений 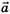 всех точек данного конца веревки. Так как изменяется и масса m1 свисающего конца веревки, и его скорость, то
всех точек данного конца веревки. Так как изменяется и масса m1 свисающего конца веревки, и его скорость, то
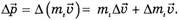
Учитывая определение ускорения и то, что
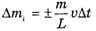
(знак «+» — при увеличении массы, знак «–» — приуменьшении массы), перепишем (5) в виде
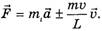 (6)
(6)
Тогда для левого конца веревки (сила T1 являетсядля него внешней) (см. рис. 2)
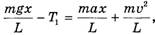 (7)
(7)
откуда с учетом (1) и (2)

Аналогично для правого конца веревки
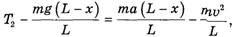
откуда с учетом (1) и (2)
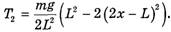 (8)
(8)
Таким образом, 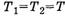 . (Сравните формулы (3) и (8).) Значит, веревка давит на блок с силой
. (Сравните формулы (3) и (8).) Значит, веревка давит на блок с силой
 (9)
(9)
При 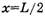 получаем
получаем 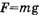 ,
,
при 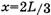 —
— 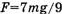 (см. выше).
(см. выше).
Решение 2. Формулу (5) применяем для всей веревки (рис. 3):
 (10)
(10)
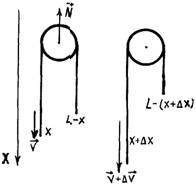
Рис. 3
Пусть за время Δt левый конец веревки сместился на Δx, а скорость его увеличилась на Δυ. Тогда с учетом направления движения концов веревки запишем проекции начального импульса

и конечного импульса всей веревки
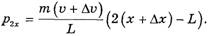
Пренебрегая слагаемым второго порядка малости, содержащим произведение 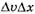 , для проекции изменения импульса имеем:
, для проекции изменения импульса имеем:
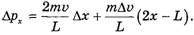
Учитывая определения скорости и ускорения и формулу (10), получим
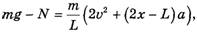
откуда
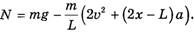
Так как по третьему закону Ньютона 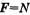 , то, учитывая (1) и (2), окончательно имеем:
, то, учитывая (1) и (2), окончательно имеем:
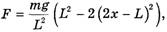
что совпадает с (9).
Проанализируем формулы (8) и (9). Решив квадратное уравнение
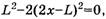
получим, что при длине левого конца веревки
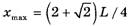
веревка перестанет действовать на блок. Очевидно, что

Таким образом, формулы (1), (2), (7)-(9) перестают быть справедливыми при 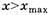 . Значит, веревка перестанет действовать на блок раньше, чем вся она соскользнет с блока и станет невесомой. При длине веревки 1 м длина короткого конца веревки в этот момент составит весьма заметную величину порядка 14 см. В этот момент модель, принятая нами, перестанет действовать. Натяжение веревки в точках 1 и 2 исчезает. Точно описать поведение всей веревки в дальнейшем мы не можем. Для этого необходимо знать силы натяжения веревки в ее различных сечениях. (Можно провести наблюдение за скольжением металлической цепочки с мелкими звеньями по стеклянной палочке и направлением падения ее верхнего конца.) Правомерно ли в таком случае требовать нахождения скорости веревки (как единого целого) в тот момент, когда она сойдет с блока (подразумевается прохождение конца вертикально расположенной веревки через точку 1),если мы не уверены в том, что все точки веревки двигаются с одинаковой линейной скоростью? А ведь именно так стоит вопрос к этой задаче в большинстве сборников задач ([1]-[3]).
. Значит, веревка перестанет действовать на блок раньше, чем вся она соскользнет с блока и станет невесомой. При длине веревки 1 м длина короткого конца веревки в этот момент составит весьма заметную величину порядка 14 см. В этот момент модель, принятая нами, перестанет действовать. Натяжение веревки в точках 1 и 2 исчезает. Точно описать поведение всей веревки в дальнейшем мы не можем. Для этого необходимо знать силы натяжения веревки в ее различных сечениях. (Можно провести наблюдение за скольжением металлической цепочки с мелкими звеньями по стеклянной палочке и направлением падения ее верхнего конца.) Правомерно ли в таком случае требовать нахождения скорости веревки (как единого целого) в тот момент, когда она сойдет с блока (подразумевается прохождение конца вертикально расположенной веревки через точку 1),если мы не уверены в том, что все точки веревки двигаются с одинаковой линейной скоростью? А ведь именно так стоит вопрос к этой задаче в большинстве сборников задач ([1]-[3]).
И последнее. Почему выражение, получаемое для ускорения из заведомо ложной системы уравнений (*), получается правильным? Очевидно, это происходит потому, что при сложении выражений, предшествующих (7) и (8), слагаемые 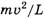 компенсируют друг друга (поскольку они имеют противоположные знаки). При этом получается точно такое же уравнение, как и при сложении уравнений системы (*).
компенсируют друг друга (поскольку они имеют противоположные знаки). При этом получается точно такое же уравнение, как и при сложении уравнений системы (*).
1. Фейнмановские лекции по физике. Задачи и упражнения. — М.: Мир, 1967.
2. Гольдфарб Н.И. Сборник вопросов и задач по физике. — М.: Высш. шк., 1975.
3. Сборник задач по физике / Под ред. С.М.Козела. — М.: Наука, 1990.
4. Гельфгат И.М., Генденштейн Л.Э., Кирик Л.А. 1001 задача по физике с ответами, указаниями, решениями. — М.: Илекса, 2001.
5. Задачи по физике / Под ред. О.Я.Савченко. — М.: Наука, 1988.
6. Корсунский Б. Внимание: ловушка! // Квант. — 1992. — № 7.
| Выложил | alsak |
| Опубликовано | 01.06.09 |
| Просмотров | 25095 |
| Рубрика | Решение задач |
| Тема | Законы сохранения Динамика |