Самсонов С.В. Что я думаю о веревке
Самсонов С.В. Что я думаю о веревке //Фiзiка: праблемы выкладання. – 2000. – № 3. – С. 76-79.
Хочу предложить мои мысли по статье А.И.Слободянюка «Заметки о веревке» (№ 1, 2000 г., с. 75).
Итак, нам дано два уравнения:
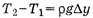 (1) и
(1) и 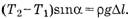 (2)
(2)
Перед нами стоит вопрос: Какое из них верно? Однако этот вопрос не совсем точен, так как звучать он должен следующим образом: Какое уравнение из двух уравнений максимально приближено к реальности? Ведь при выводе обоих уравнений было допущено округление — считалось, что обе силы натяжения: и T1, и Т2 (см. рис. в № 1, 2000 г.) направлены вдоль одной линии, однако эти силы направлены так, как показано на рисунке 1.
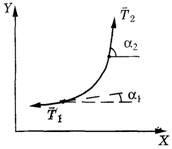
Рис. 1
И даже при маленьком участке длиной Δl  , ведь иначе при T2 > T1и
, ведь иначе при T2 > T1и 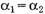 выделенный участок должен двигаться вправо.
выделенный участок должен двигаться вправо.
Итак, округление не дало единого правильного ответа, поэтому попробуем разрешить данную проблему точными методами.
Запишем условие равновесия в проекции на ось Y
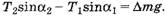 (3)
(3)
И на ось X:
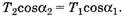 (4)
(4)
Возведем уравнение (4) в квадрат:
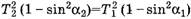 или
или
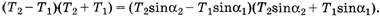
Теперь, учитывая, что Δm очень мало и, следовательно, 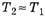 , а
, а 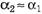 (конечно же, совсем без округления тоже не обойтись), получим:
(конечно же, совсем без округления тоже не обойтись), получим:
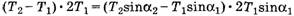 или
или
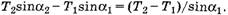
Откуда, учитывая уравнение (3), получим:
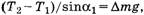
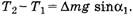
Теперь обозначим α1 просто α и учтем, что  Тогда:
Тогда:
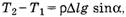
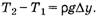
То есть правильное все-таки первое уравнение!!!
Можно это доказать и качественно. Для этого посмотрим на рисунок 2.

Рис. 2
На нем линия OO1— направление выделенного участка. 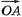 и
и 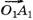 — силы, которые реально действуют на этот участок. Если же считать что
— силы, которые реально действуют на этот участок. Если же считать что 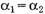 , то надо считать, что эти силы действуют вдоль направления участка, то есть мы при округлении заменяем реальные силы на силы
, то надо считать, что эти силы действуют вдоль направления участка, то есть мы при округлении заменяем реальные силы на силы 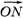 и
и 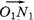 , причем
, причем 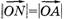 и
и 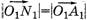 .
.
Итак, первый случай — мы проецируем все силы на направление участка. При этом нас интересует разность проекций реальных сил 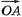 и
и 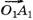 — ОВ и O1B1.
— ОВ и O1B1.
Считая, что 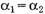 и, следовательно, считая, что силы
и, следовательно, считая, что силы 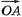 и
и 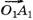 действуют вдоль направления участка, мы увеличиваем ОВ и O1B1 на ВN и В1N1 соответственно. Но так как мы увеличиваем обе проекции, их разность при этом не изменяется.
действуют вдоль направления участка, мы увеличиваем ОВ и O1B1 на ВN и В1N1 соответственно. Но так как мы увеличиваем обе проекции, их разность при этом не изменяется.
Теперь рассмотрим второй случай, — мы проецируем все силы на ось Y. Теперь нас интересует разность проекций реальных сил 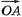 и
и 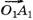 на ось Y — ОС и О1C1.
на ось Y — ОС и О1C1.
Считая, что 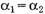 , и, следовательно, считая, что силы
, и, следовательно, считая, что силы  и
и  действуют вдоль направления участка, мы уменьшаем большую проекцию О1C1 и увеличиваем меньшую проекцию ОС. Следовательно, разность проекций О1C1 – ОС значительно уменьшается.
действуют вдоль направления участка, мы уменьшаем большую проекцию О1C1 и увеличиваем меньшую проекцию ОС. Следовательно, разность проекций О1C1 – ОС значительно уменьшается.
Теперь понятно, почему второй способ дает неправильный ответ.
А сейчас поговорим еще о том, почему уравнение (1) похоже на формулу для гидростатического давления (а оно действительно похоже).
Рассмотрим принцип работы идеального блока (см. рис. 3).
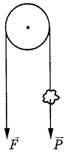
Рис. 3
Пусть на одном конце веревки висит груз весом  , а мы тянем за другой конец с силой
, а мы тянем за другой конец с силой 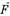 . Значит, на груз вверх действует такая же по модулю сила
. Значит, на груз вверх действует такая же по модулю сила  . Найдем механическое напряжение веревки σ1 около наших рук и σ2 около груза:
. Найдем механическое напряжение веревки σ1 около наших рук и σ2 около груза:
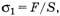
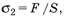
то есть 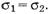
Но механическое напряжение имеет смысл продольного давления в веревке! То есть давление (продольное), оказываемое на конец веревки, без изменения передается в другую часть веревки, причем независимо от того, какую форму имеет веревка (при этом сечение веревки должно быть одинаковым). А это есть не что иное, как закон Паскаля (правда, в применении к веревке). И было бы даже удивительно, если бы формула (1) не была похожа на формулу для гидростатического давления.
В соответствии с вышесказанным можно привести еще одно решение первоначальной задачи. На кусочек массой Δm (см. рис. 4) действует сила тяжести, проекция которой на направление нити равна:
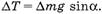
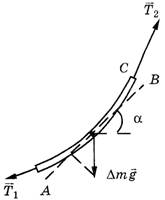
Рис. 4
А так как 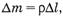 то
то
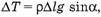
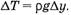
Следовательно, этот кусочек действует на некоторое сечение С с силой  . Просуммировав действие таких кусочков от точки А до точки В, получим:
. Просуммировав действие таких кусочков от точки А до точки В, получим:
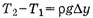 .
.
Мы опять-таки получили формулу (1)!!!
| Выложил | alsak |
| Опубликовано | 07.06.09 |
| Просмотров | 12212 |
| Рубрика | Решение задач |
| Тема | Динамика |