Зайцев И.А. Кинематика // Квант
Зайцев И.А. Кинематика // Квант. — 1971. — № 9. — С. 47-51.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Как вы решаете задачи на кинематику? Сколько формул вы помните? 5? 10? 15? Очень часто решение задач начинается с выписывания большого количества формул — формулы для пути, пройденного телом за n-ю секунду, формулы для отношения путей, пройденных телом за последовательные промежутки времени, формулы для разности квадратов скоростей тела и так далее. Затем эти формулы пытаются подставлять друг в друга, делить, множить... Иногда таким способом удается найти ответ. Но чаще всего задачи на кинематику — непреодолимая преграда. Это, пожалуй, один из самых трудных разделов для абитуриентов. Хотя должен быть одним из самых простых. Давайте разберемся в нем.
Будем сначала говорить о прямолинейном движении тела. Если прямую, вдоль которой оно движется, принять за ось координат 0Х (точка 0 — начало координат), то положение тела определяется его координатой х. При движении с постоянным ускорением координата тела меняется со временем по закону
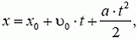 (*)
(*)
где х0 — начальная координата тела (при t = 0), υ0 — его начальная скорость и а — ускорение. Уравнение (*) и есть кинематическое уравнение движения тела. Конечно, уравнение (*) — проекция на ось х векторного уравнения для радиуса-вектора ![]() , определяющего положение центра масс тела (рис. 1). Поэтому проекция на ось ОХ тех векторных величин, которые направлены так же, как и ось ОХ, положительны, а тех, которые направлены в противоположную сторону,— отрицательны. Это нужно учитывать, подставляя эти величины в уравнение (*).
, определяющего положение центра масс тела (рис. 1). Поэтому проекция на ось ОХ тех векторных величин, которые направлены так же, как и ось ОХ, положительны, а тех, которые направлены в противоположную сторону,— отрицательны. Это нужно учитывать, подставляя эти величины в уравнение (*).
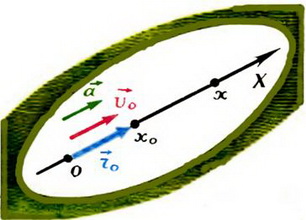
Рис. 1.
Подчеркнем еще раз: уравнение (*) — уравнение для координаты тела, а не для пути, пройденного им. Путь — положительная скалярная величина, которая не может уменьшаться. В то же время, координата тела может вести себя как угодно. Например, если υ0 положительно и 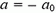 отрицательно (вектор скорости
отрицательно (вектор скорости 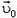 направлен в ту же сторону, что и ось ОХ, а вектор ускорения
направлен в ту же сторону, что и ось ОХ, а вектор ускорения 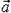 — в противоположную), то координата тела вначале будет увеличиваться, а затем уменьшаться. Это сразу видно из графика зависимости х от t (рис. 2). Через некоторое время после начала движения координата станет отрицательной. Только в том случае, когда тело движется в одну сторону, путь, пройденный телом, равен абсолютному значению изменения его координаты. Поэтому, если нам нужно найти путь, пройденный телом за какое-то время, приходится разбивать движение на участки, на которых тело двигалось в одну сторону, находить изменения координаты тела на этих участках и складывать их абсолютные величины. Но в этом нет необходимости, если нас интересуют другие величины — координата, время, скорость и ускорение. Нужно просто воспользоваться кинематическим уравнением движения (*).
— в противоположную), то координата тела вначале будет увеличиваться, а затем уменьшаться. Это сразу видно из графика зависимости х от t (рис. 2). Через некоторое время после начала движения координата станет отрицательной. Только в том случае, когда тело движется в одну сторону, путь, пройденный телом, равен абсолютному значению изменения его координаты. Поэтому, если нам нужно найти путь, пройденный телом за какое-то время, приходится разбивать движение на участки, на которых тело двигалось в одну сторону, находить изменения координаты тела на этих участках и складывать их абсолютные величины. Но в этом нет необходимости, если нас интересуют другие величины — координата, время, скорость и ускорение. Нужно просто воспользоваться кинематическим уравнением движения (*).
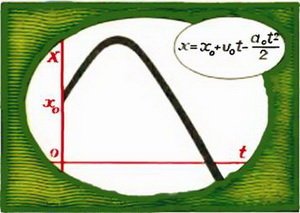
Рис. 2.
Решим с его помощью следующую задачу.
Задача 1. Камень брошен вертикально вверх. Через какое время он упадет на землю?
Выберем ось координат, направленную вертикально вверх, с началом координат, связанным с землей. В этом случае 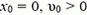 и
и 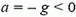 . Поэтому
. Поэтому
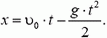 (1)
(1)
В момент падения на землю 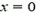 . Подставляя это значение х в кинематическое уравнение движения камня (1), получим уравнение
. Подставляя это значение х в кинематическое уравнение движения камня (1), получим уравнение
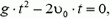
решая которое, найдем
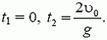
Значение 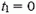 соответствует моменту бросания камня; t2 — время движения камня.
соответствует моменту бросания камня; t2 — время движения камня.
Конечно, уравнение движения определяет координату тела в любой момент времени. Воспользовавшись этим, найдем, например, тот момент времени, когда камень находился на высоте h. Подставляя в уравнение движения х = h, получим
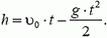
Отсюда
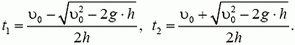
На высоте h тело было дважды — в момент tl при подъеме и в момент t2 при спуске (конечно, 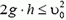 , так как максимальная высота подъема тела
, так как максимальная высота подъема тела 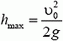 ).
).
Часто нам нужно знать скорость тела в разные моменты времени. Так как 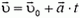 , то для проекции скорости на ось ОХ имеем
, то для проекции скорости на ось ОХ имеем
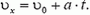 (**)
(**)
Это второе кинематическое уравнение движения — уравнение скорости. Оно, конечно, тоже справедливо во все время движения тела, если только ускорение а было постоянным.
Найдем, например, скорость камня в момент падения на землю. В этом случае 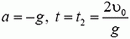 . Поэтому
. Поэтому
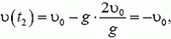
то есть в момент падения на землю скорость камня равна начальной, но направлена в противоположную сторону.
Уравнение (**) позволяет легко найти время tп подъема камня. Так как в точке максимального подъема скорость камня равна нулю, то
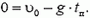
Отсюда 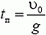 . Время подъема камня равно половине времени полета.
. Время подъема камня равно половине времени полета.
Мы видим, что два уравнения — для координаты и для скорости позволяют получить ответ на любой вопрос относительно движения камня. Именно их и нужно всегда помнить.
Решим еще одну задачу.
Задача 2. Свободно падающее тело за последнюю секунду прошло 1/3 своего пути. Сколько секунд (n) и с какой высоты (h) падало тело?
Примем за начало координат точку бросания, а ось координат направим вертикально вниз. Тогда координата тела зависит от времени по закону
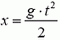 (1)
(1)
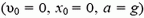 . Если тело падало n секунд, время падения равно
. Если тело падало n секунд, время падения равно 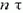 (τ = 1 с), и
(τ = 1 с), и
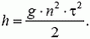 (2)
(2)
Через время 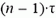 после начала движения координата тела была равна 2/3 h. Поэтому
после начала движения координата тела была равна 2/3 h. Поэтому
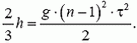
Решая уравнения (1) и (2) совместно, найдем,
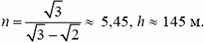
Можно было выбрать и другую систему координат, например, связанную с землей и осью координат, направленной вверх. Тогда уравнение движения тела было бы таким:
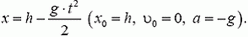
Здесь при 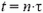 координата
координата  , а при
, а при 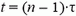 —
— 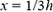 .
.
Можно выбрать и еще одну систему координат — с началом в точке бросания и осью, направленной вверх. В этой системе
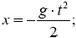
при 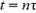 координата
координата 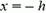 , при
, при 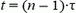 —
— 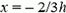 .
.
В данной задаче выбор системы координат не очень существен, но часто, удачно выбрав систему координат, можно значительно упростить решение.
Решим, например, такую задачу.
Задача 3. С каким промежутком времени τ оторвались от крыши две дождевые капли, если через время t0 после начала падения второй капли расстояние между каплями было равно l?
Эту задачу можно, конечно, решать в системе координат, связанной с крышей (сделайте это сами).
Но удобнее перейти к системе координат, связанной со второй каплей. Так как капли падают с одинаковым ускорением относительно земли, то их относительное ускорение равно нулю: капли движутся друг относительно друга равномерно. Их относительная скорость равна скорости первой капли относительно земли в момент отрыва второй капли 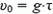 . Уравнение движения первой капли в системе координат, связанной со второй, выглядит так:
. Уравнение движения первой капли в системе координат, связанной со второй, выглядит так:
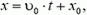
где 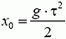 . При
. При 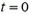 —
— 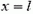 , то есть
, то есть
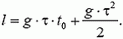
Решив это уравнение, получим ответ:
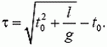
Решим еще такую задачу.
Задача 4. Снаряд взрывается в некоторой точке траектории. На какой поверхности будут находиться осколки снаряда через некоторое время t после взрыва?
В системе координат, связанной с точкой взрыва снаряда и движущейся с той же скоростью, что и снаряд, и с тем же ускорением относительно земли, осколки снаряда движутся равномерно. Поэтому через время t каждый из них будет находиться на расстоянии 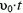 от точки взрыва (υ0 — скорость осколков в нашей системе координат), то есть все они будут находиться на сфере радиуса
от точки взрыва (υ0 — скорость осколков в нашей системе координат), то есть все они будут находиться на сфере радиуса 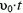 с центром в точке взрыва снаряда.
с центром в точке взрыва снаряда.
Попробуйте решить эту задачу в системе координат, связанной с землей.
В заключение разберем случай, когда тело движется по криволинейной плоской траектории с постоянным ускорением 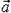 . В этом случае, спроектировав скорость
. В этом случае, спроектировав скорость 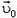 и ускорение
и ускорение 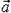 тела на два взаимно перпендикулярных направления — на оси ОХ и OY, получим два однотипных уравнения движения:
тела на два взаимно перпендикулярных направления — на оси ОХ и OY, получим два однотипных уравнения движения:
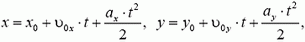
и два уравнения для скорости υ тела:
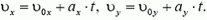
(Если траектория движения тела не лежит в одной плоскости, то мы должны записать три уравнения.)
Решим с помощью этих уравнений следующую задачу.
Задача 5. Самолет летит горизонтально на высоте h со скоростью υ0. Летчик должен сбросить бомбу в цель, лежащую впереди самолета. Под каким углом α к горизонту он должен видеть цель в момент сбрасывания бомбы?
Выберем неподвижную относительно земли систему координат с началом координат в точке, в которой находился самолет в момент сбрасывания бомбы (рис. 3).
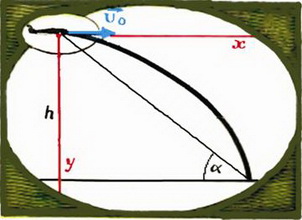
Рис. 3.
Начальная скорость бомбы равна 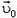 и горизонтальна, а ускорение
и горизонтальна, а ускорение 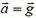 направлено вдоль оси у. Поэтому
направлено вдоль оси у. Поэтому
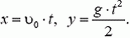
В момент t0 падения бомбы на землю в выбранной нами системе координат 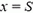 , a
, a 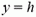 (рис. 4), поэтому
(рис. 4), поэтому
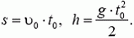
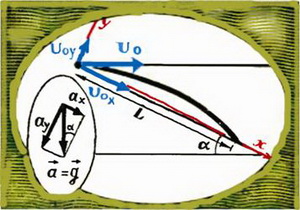
Рис. 4.
Исключая t0, получим
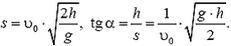
Решим еще одну задачу.
Задача 6. Камень бросают горизонтально со скоростью υ0 с горы, уклон которой равен α. На каком расстоянии L от места бросания камень упадет на землю?
В системе координат, показанной на рисунке 4, положение камня в момент времени t определяется координатами
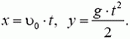
В момент t0 падения на землю 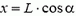 , a
, a 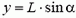 , то есть
, то есть
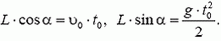
Отсюда
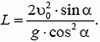
Можно было бы выбрать и другую систему координат, например, показанную на рисунке 5. Иногда это бывает удобно. В этой системе координат
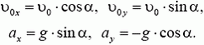
Поэтому
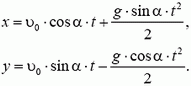
Подставляя в эти уравнения значения х и у при 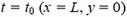 и решая их совместно, найдем ответ.
и решая их совместно, найдем ответ.
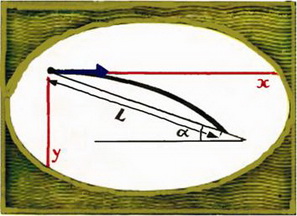
Рис. 5.
Упражнения
1. Камень свободно падает с высоты h. За какое время он проходит последний метр своего пути?
2. Камень, брошенный вертикально вверх, на высоте h побывал дважды с интервалом времени τ. С какой начальной скоростью он был брошен?
3. Камень бросают вертикально вверх со скоростью υ0 с высоты h от поверхности земли. В этот же момент с земли со скоростью υ0, бросают вертикально другой камень. Через какое время камни окажутся на одной высоте? Какова будет эта высота?
4. Цель, находящаяся на вершине холма, видна под углом α к горизонту с того места, где находится орудие. Как должен быть направлен ствол орудия к горизонту, чтобы попадание было точным, если начальная скорость снаряда υ0, а высота холма равна h?
5. Камень бросают в реку. Какой будет картина воли? Нарисуйте ее.
6. Два автомобиля одновременно прошли перекресток и едут по улицам, составляющим угол α друг с другом (рис. 6). Скорости автомобилей равны υ1 и υ2. Через какое время расстояние между автомобилями будет равно l?
Указание. Удобно выбрать систему координат, связанную с одним из автомобилей. В ней скорость второго автомобиля постоянна и равна
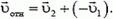
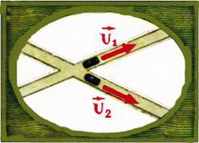
Рис. 6.
| Выложил | alsak |
| Опубликовано | 10.07.09 |
| Просмотров | 11632 |
| Рубрика | Решение задач |
| Тема | Кинематика |