Шеронов А. Аэро- и гидростатика // Квант
Шеронов А. Аэро- и гидростатика // Квант. — 1996. — № 3. — С. 53-55.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Решение задач из этого раздела физики основывается на законах Архимеда и Паскаля. По закону Паскаля давление в жидкостях и газах передается во все стороны одинаково. Если при этом газ или жидкость находятся в поле тяжести, то давления в точках с разностью координат по высоте h отличаются на ![]() , где ρ — плотность жидкости или газа, g — ускорение свободного падения. По закону Архимеда выталкивающая сила, действующая на тело, погруженное в жидкость или газ, в поле тяжести, равна весу жидкости или газа, вытесненного этим телом.
, где ρ — плотность жидкости или газа, g — ускорение свободного падения. По закону Архимеда выталкивающая сила, действующая на тело, погруженное в жидкость или газ, в поле тяжести, равна весу жидкости или газа, вытесненного этим телом.
Ниже мы рассмотрим несколько характерных примеров использования этих законов при решении задач.
Задача 1. Температура кипения воды зависит от давления окружающего воздуха. При увеличении или уменьшении давления воздуха на Δр = 27 мм рт. ст. вблизи атмосферного давления температура кипения вблизи 100 °С увеличивается или уменьшается на ΔТ0 = 1 °С. При какой температуре кипит вода в ресторане «Седьмое небо» на высоте h =330 м от поверхности Земли?
Разность давлений у поверхности Земли и на высоте h есть ![]() , где ρ — плотность воздуха при давлении р = 105 Па и температуре Т = 290 К, которая определяется уравнением состояния:
, где ρ — плотность воздуха при давлении р = 105 Па и температуре Т = 290 К, которая определяется уравнением состояния:
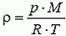
(R — газовая постоянная, М — молярная масса воздуха). Таким образом, температура кипения на высоте h уменьшается на
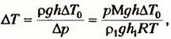
где ρ1 = 13,6•103 кг/м3 — плотность ртути, h1 = 27•10-3 м, g = 9,8 м/с2, М = 29•10-3 кг/моль, R = 8,31 Дж/(моль•К). Подставив числовые значения, получим ΔT» 1 ºC, следовательно, температура кипения на высоте 330 м равна приблизительно 99 °С.
Задача 2. В последние годы приобрело большую популярность катание на воздушных шарах. Подъемная сила создается путем подогрева воздуха в оболочке шара газовой горелкой. Объем шара и давление воздуха в нем остаются при этом практически постоянными. Оцените, каким должен быть объем шара, чтобы при нагреве воздуха в нем на Δt = 30 °С относительно окружающей атмосферы он смог поднять полезный груз массой т = 150 кг (масса оболочки, корзины, человека и т.д.).
Выталкивающая сила, равная весу вытесненного шаром холодного атмосферного воздуха, уравновешивается силой тяжести полезного груза и теплого воздуха, находящегося в оболочке шара. Пусть Т1 = 290 К — температура атмосферы, Т2 = 320 К — температура воздуха в шаре. Из уравнения состояния газа и условия плавания шара находим его объем: масса холодного воздуха 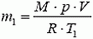 , масса горячего воздуха
, масса горячего воздуха 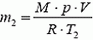 , по условию
, по условию 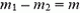 .
.
Окончательно имеем
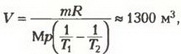
где М = 29·103 кг/моль — молярная масса воздуха, р = 105 Па — атмосферное давление, R= 8,31 Дж/(моль·К) — газовая постоянная.
Задача 3. По некоторым оценкам масса озона (О3), содержащегося в атмосфере Венеры, составляет α = 10–5 % массы всей атмосферы. Какой толщины слой образовал бы озон, если бы он собрался у поверхности планеты и имел температуру и давление, равные температуре и давлению атмосферы у поверхности Венеры? Ускорение свободного падения на Венере g = 8,2 м/с2, температура вблизи поверхности Т = 800 К.
Пусть m — масса атмосферы Венеры, М = 48 г/моль —молярная масса озона, R = 8,31 Дж/(моль·К) — газовая постоянная. Озон вблизи поверхности занимает объем 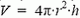 при давлении р и температуре Т. По условию
при давлении р и температуре Т. По условию 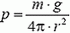 , где r — радиус Венеры. С другой стороны, уравнение состояния для озона имеет вид
, где r — радиус Венеры. С другой стороны, уравнение состояния для озона имеет вид
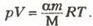
Подставив сюда выражения для V и р, получим искомую толщину слоя озона
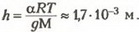
Задача 4. Колокол для подводных работ представляет собой тонкостенный цилиндрический стакан, который опускается вверх дном с борта катера на дно водоема. Какова должна быть толщина стенок и дна колокола, чтобы он мог покоиться на дне водоема глубиной Н = 3 м? Внутренний радиус колокола r = 1 м, высота h = 2м, плотность стали ρст = 7,8·103 кг/м3.
Предположим, что в момент касания колоколом дна водоема между ними есть тонкая водяная прослойка (рис. 1).
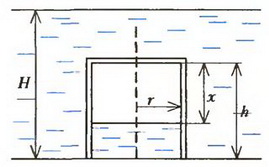
Рис. 1.
Для простоты толщину Δ стенок и дна колокола будем считать одинаковой и малой по сравнению с его радиусом и высотой. Вес воды, вытесненной колоколом, определяется объемом воздушной прослойки 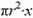 и объемом боковых стенок и дна колокола
и объемом боковых стенок и дна колокола 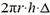 и
и 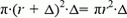 . Толщина стенок Δ определяется условием, что сила тяжести колокола не меньше выталкивающей силы, т.е.
. Толщина стенок Δ определяется условием, что сила тяжести колокола не меньше выталкивающей силы, т.е.
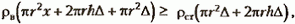 (*)
(*)
где ρв = 103 кг/м3 — плотность воды. Найдем теперь толщину х воздушной прослойки, оставшейся у «потолка» в момент касания колоколом дна водоема. Воздух в колоколе находится под давлением 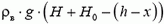 , где g — ускорение свободного падения,
, где g — ускорение свободного падения, 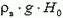 — наружное атмосферное давление (H0 = 10,3 м). По закону Бойля — Мариотта имеем
— наружное атмосферное давление (H0 = 10,3 м). По закону Бойля — Мариотта имеем
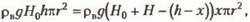
откуда получаем
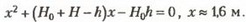
Окончательно из неравенства (*) для толщины стенок находим
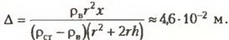
Приведем еще один расчет величины максимальной выталкивающей силы — с использованием закона Паскаля. Воздух в колоколе действует снизу на внутреннюю поверхность дна площадью 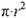 с силой
с силой 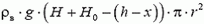 . На поверхность соприкосновения колокола с дном площадью
. На поверхность соприкосновения колокола с дном площадью 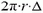 действует снизу сила, равная
действует снизу сила, равная 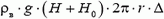 . Сверху на дно колокола площадью
. Сверху на дно колокола площадью 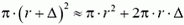 действует сила
действует сила 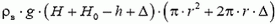 . Выталкивающая сила равна разности сил давления снизу и сверху:
. Выталкивающая сила равна разности сил давления снизу и сверху:
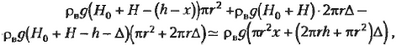
что совпадает с величиной, приведенной в выражении (*).
Задача 5. Вертикально расположенная U-образная трубка частично заполнена жидкостью так, что расстояния от открытых концов трубки до уровня жидкости в коленах равны h0. Какой максимальный по толщине слой более легкой жидкости можно налить в одно из колен трубки, чтобы жидкость из трубки не выливалась? Отношение плотностей жидкостей равно k (k > 1). Жидкости не смешиваются.
Пусть в правое колено трубки налита более легкая жидкость плотностью ρ1 и толщиной слоя h1 (рис. 2). В другом колене ее уравновешивает слой первоначально налитой жидкости плотностью ρ2 и толщиной h2, так что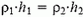 . В колене с тяжелой жидкостью остался незаполненым слой толщиной
. В колене с тяжелой жидкостью остался незаполненым слой толщиной
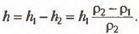
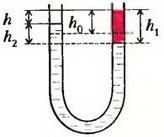
Рис. 2
Заметим, наконец, что имеет место очевидное равенство
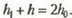
Окончательно для h1 находим
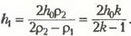
Задача 6. Плотность стратифицированной жидкости меняется с глубиной h по закону 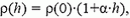 где ρ(0) — известная константа. Для измерения константы α в жидкость опускают тяжелый цилиндр длиной l и сечением S, который висит вертикально на нити, привязанной к динамометру. Разность показаний динамометра равна ΔF в положениях, когда верхняя грань цилиндра совпадает с поверхностью жидкости и когда она же находится на глубине h = l от поверхности. Найдите по этим данным величину α.
где ρ(0) — известная константа. Для измерения константы α в жидкость опускают тяжелый цилиндр длиной l и сечением S, который висит вертикально на нити, привязанной к динамометру. Разность показаний динамометра равна ΔF в положениях, когда верхняя грань цилиндра совпадает с поверхностью жидкости и когда она же находится на глубине h = l от поверхности. Найдите по этим данным величину α.
Разность показаний динамометра определяется разностью давлений на верхнюю и нижнюю грани цилиндра, находящегося в жидкости. Так как плотность жидкости меняется с глубиной по линейному закону, давление меняется с глубиной по закону
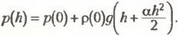
Если m — масса цилиндра, то в первом случае показание динамометра равно
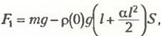
а во втором —
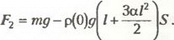
По условию
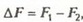
откуда находим
Разность показаний динамометра, а следовательно, и константу α можно найти и с помощью закона Архимеда, определив вес жидкости, вытесненной цилиндром в первом и втором случаях. Сделайте это самостоятельно.
Задача 7. Изогнутая трубка постоянного внутреннего сечения с открытыми концами расположена так, что ее прямолинейные участки вертикальны (рис. 3). Трубка заполнена двумя несмешивающимися жидкостями плотностью ρ1 снизу и ρ2 сверху (ρ1 > ρ2). Все границы раздела между жидкостями расположены на одном уровне горизонта, свободные поверхности жидкости в крайних коленах также находятся на одном горизонтальном уровне. При каких соотношениях между величинами плотностей ρ1 и ρ2 такое положение жидкостей устойчиво?
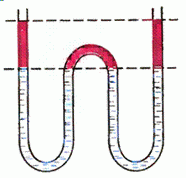
Рис. 3.
Выведем жидкость из равновесия, сместив уровень в правом колене на х вниз (рис. 4).
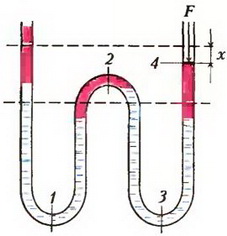
Рис. 4.
Найдем силу F, которую надо прикладывать к воображаемому невесомому поршню в этом колене для поддержания равновесия. Если получится F > 0, то равновесие будет устойчивым.
Изменение давления под поршнем найдем из цепочки уравнений для сечений 1–4:
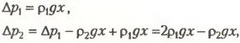
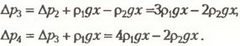
Так как 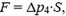 из условия F > 0 получим ответ:
из условия F > 0 получим ответ:
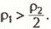
Условие устойчивости можно найти и через энергию: в положении устойчивого равновесия потенциальная энергия должна быть минимальной. При смещении уровня на х изменение потенциальной энергии равно 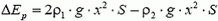 , тогда из условия ΔЕр > 0 получаем
, тогда из условия ΔЕр > 0 получаем 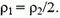
Упражнения
1. Атмосфера Венеры состоит в основном из углекислого газа, давление которого у поверхности достигает р = 20 атм, а температура составляет Т = 800 К. Оцените массу углекислого газа на Венере, считая, что толщина атмосферы много меньше радиуса планеты r = 6300 км. Какой толщины была бы атмосферы Венеры, если бы давление и температура ее были равны соответствующим значениям вблизи поверхности? Ускорение свободного падения на Венере g = 8,2 м/с2, газовая постоянная R = 8,31 Дж/(моль•К), молярная масса СО2 равна М = 44 г/моль.
2. В горизонтальной закрытой с одного конца трубке столбиком ртути длиной l = 12 см заперт слой воздуха толщиной L = 35 см. Если трубку повернуть один раз открытым концом вниз, а другой раз вверх, то столбик ртути смещается. Разность этих смещений от начального горизонтального положения составляет Δx = 2 см. Найдите величину наружного атмосферного давления (в см рт. ст.).
3. В мензурку с водой, стоящую вертикально, опустили вверх дном тонкостенную пробирку длиной l0. В результате уровень воды в мензурке поднялся на ΔН, а пробирка стала плавать в вертикальном положении (рис. 5). Найдите толщину слоя воды, зашедшей в пробирку, и длину части пробирки, находящейся над водой. Отношение площади сечения мензурки к площади сечения пробирки равно k (k > 1). Атмосферное давление р, плотность воды ρ, ускорение свободного падения g.
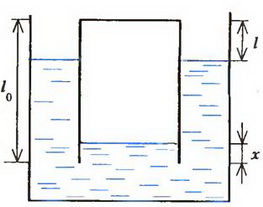
Рис. 5.
Ответы.
1. 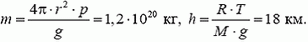
2. 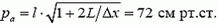
3. 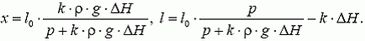
| Выложил | |
| Опубликовано | 01.08.16 |
| Просмотров | 7769 |
| Рубрика | Решение задач |
| Тема | Гидростатика |