Кочеров Г.Г. Расчёт электрических цепей
Кочеров Г. Г. Расчёт электрических цепей // Фiзiка: праблемы выкладання. – 2009. – № 3. – С. 24–25.
Для развития творческих способностей учащихся представляют интерес задачи на решение резисторных схем постоянного тока методом равнопотенциальных узлов. Решение этих задач сопровождается последовательным преобразованием исходной схемы. Причём наибольшее изменение она претерпевает после первого шага, когда используется данный метод. Дальнейшие преобразования связаны с эквивалентной заменой последовательных или параллельных резисторов.
Для преобразования цепи пользуются тем свойством, что во всякой цепи точки с одинаковыми потенциалами можно соединять в узлы. И наоборот: узлы цепи можно разделить, если после этого потенциалы точек, входящих в узел, не изменятся.
В методической литературе часто пишут так: если схема содержит проводники с одинаковыми сопротивлениями, расположенными симметрично относительно какой-либо оси или плоскости симметрии, то точки этих проводников, симметричные относительно этой оси или плоскости, имеют одинаковый потенциал. Но вся сложность в том, что такую ось или плоскость никто на схеме не обозначает и отыскать её непросто.
Предлагаю другой, упрощённый способ решения подобных задач.
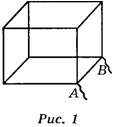
Задача 1. Проволочный кубик (рис. 1) включён в цепь между точками А к В.
Найдите его общее сопротивление, если сопротивление каждого ребра равно R.
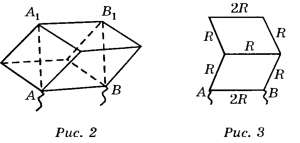
Поставим кубик на ребро АВ (рис. 2) и "распилим" его на две параллельные половинки плоскостью АА1B1В, проходящей через нижнее и верхнее ребро.
Рассмотрим правую половинку куба. Учтём, что нижнее и верхнее ребро расщепились пополам и стали в 2 раза тоньше, а их сопротивления увеличились в 2 раза и стали по 2R (рис. 3).
1) Находим сопротивление R1 трёх верхних проводников, соединённых последовательно:
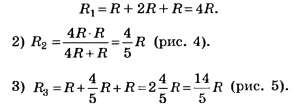
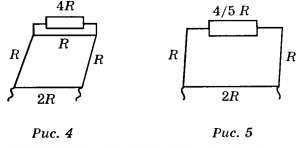
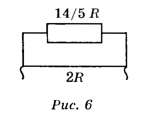
4) Находим общее сопротивление этой половинки куба (рис. 6):
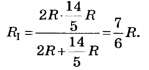
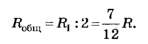
Получилось сравнительно просто, понятно и доступно для всех.
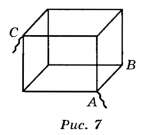
Задача 2. Проволочный кубик подключён в цепь не ребром, а диагональю АС любой грани. Найдите его общее сопротивление, если сопротивление каждого ребра равно R (рис. 7).
Снова ставим кубик на ребро АВ. "Распиливаем" кубик на две параллельные половинки той же вертикальной плоскостью (см. рис. 2).
Опять рассматриваем правую половинку проволочного куба. Учитываем, что верхнее и нижнее ребро расщепились пополам и их сопротивления стали по 2R.
С учётом условия задачи имеем следующее соединение (рис. 8).
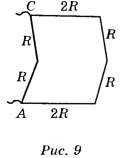
Дальше ещё проще. Так как ток по ребру а—b не идёт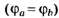
, то это ребро из цепи можно удалить (рис. 9).
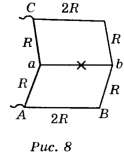
1) Находим R1= 2R + R + R + 2R = 6R.
2) R2= R + R = 2R.
3) Общее сопротивление половинки куба
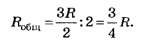
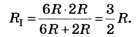
Эти приёмы решения задач представляют интерес для развития творческих способностей учащихся. Их можно использовать при подготовке учеников к школьным и районным олимпиадам.
| Выложил | alsak |
| Опубликовано | 02.03.12 |
| Просмотров | 8832 |
| Рубрика | Решение задач |
| Тема | Постоянный ток |