Жилко В.В., Маркович Л.Г. Закон сложения скоростей
Жилко В.В., Маркович Л.Г. Закон сложения скоростей при поступательном и непоступательном движении подвижной системы отсчёта // Фізіка: праблемы выкладання. — 2009. — № 5. — С. 44-50.
Рассмотрим две инерциальные системы отсчёта К и К' (рис. 1), причём К' движется относительно К поступательно со скоростью 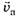 в направлении OO'. Пусть в начальный момент времени t0 = 0 их оси и начала координат О и О' совпадали. Это означает, что
в направлении OO'. Пусть в начальный момент времени t0 = 0 их оси и начала координат О и О' совпадали. Это означает, что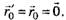
Неподвижную систему К в подобной ситуации называют абсолютной, а движущуюся относительно ее систему К' — относительной. Движение материальных точек относительно абсолютной системы называют абсолютным, а относительно движущейся — относительным.
Движение материальной точки в относительной системе называют переносным движением. На рисунке 1 система хуr является абсолютной (неподвижной), а система х'у'r' — относительной (движущейся).
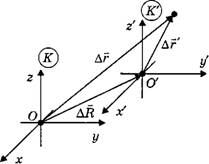
Если система отсчёта К' через промежуток времени ∆t переместится на 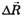 и займёт новое положение в пространстве, то материальная точка М за этот же промежуток времени ∆t переместится относительно К и К' соответственно на
и займёт новое положение в пространстве, то материальная точка М за этот же промежуток времени ∆t переместится относительно К и К' соответственно на 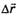 и
и 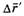 (см. рис. 1). Как видно из рисунка 1,
(см. рис. 1). Как видно из рисунка 1,
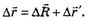
Исходя из этого соотношения можно сформулировать принцип суперпозиции (правило сложения) перемещений:
перемещение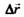 материальной точки за данный промежуток времени ∆t относительно неподвижной системы отсчёта К равно векторной сумме её перемещения
материальной точки за данный промежуток времени ∆t относительно неподвижной системы отсчёта К равно векторной сумме её перемещения 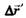 относительно подвижной системы отсчёта К' и перемещения
относительно подвижной системы отсчёта К' и перемещения 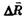 подвижной системы отсчёта К' относительно неподвижной К.
подвижной системы отсчёта К' относительно неподвижной К.
Разделим обе части этого равенства на промежуток времени ∆t :
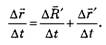
Отсюда с учётом определения средних скоростей находим
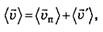
где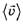 — средняя скорость перемещения материальной точки относительно К,
— средняя скорость перемещения материальной точки относительно К, 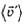 — относительно К', а
— относительно К', а 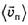 — средняя скорость перемещения системы отсчёта К' относительно К.
— средняя скорость перемещения системы отсчёта К' относительно К.
Если промежуток времени ∆t уменьшать так, чтобы он стремился к нулю, то в результате придём к мгновенным скоростям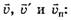
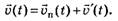
Таким образом, получили закон сложения скоростей Галилея:
скорость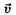 материальной точки относительно неподвижной системы отсчёта К равна векторной сумме её скорости
материальной точки относительно неподвижной системы отсчёта К равна векторной сумме её скорости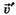 относительно подвижной системы отсчёта К' и скорости подвижной системы
относительно подвижной системы отсчёта К' и скорости подвижной системы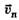 К' относительно неподвижной К.
К' относительно неподвижной К.
Отметим, что этот закон справедлив для нерелятивистских скоростей движения 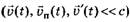 и когда движение системы отсчёта К' относительно К является поступательным.
и когда движение системы отсчёта К' относительно К является поступательным.
Отметим, что, так как любое данное перемещение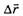 можно представить в виде суммы двух произвольных перемещений
можно представить в виде суммы двух произвольных перемещений 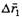 и
и 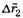 таким образом, чтобы
таким образом, чтобы
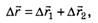
то и скорость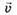 можно представить в виде векторной суммы двух скоростей:
можно представить в виде векторной суммы двух скоростей:
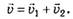
Но каким будет закон сложения скоростей, если движение подвижной системы отсчёта относительно неподвижной непоступательное'?
Для ответа на этот вопрос, рассмотрим движение жука по вращающемуся диску. Пусть диск радиусом R вращается с постоянной угловой скоростью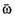 вокруг неподвижной оси, проходящей через центр О диска, перпендикулярно к нему (рис. 2). Вдоль радиуса диска от центра к его краю ползёт жук с постоянной относительно диска скоростью
вокруг неподвижной оси, проходящей через центр О диска, перпендикулярно к нему (рис. 2). Вдоль радиуса диска от центра к его краю ползёт жук с постоянной относительно диска скоростью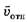 . Определим скорость
. Определим скорость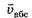 относительно неподвижной системы отсчёта в тот момент времени, когда жук находится на расстоянии r от оси диска. Для этого свяжем неподвижную систему отсчёта с листом бумаги, относительно которого диск вращается. Как следует из рисунка 2, мгновенная скорость жука
относительно неподвижной системы отсчёта в тот момент времени, когда жук находится на расстоянии r от оси диска. Для этого свяжем неподвижную систему отсчёта с листом бумаги, относительно которого диск вращается. Как следует из рисунка 2, мгновенная скорость жука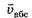 относительно неподвижной системы отсчёта равна векторной сумме скорости жука
относительно неподвижной системы отсчёта равна векторной сумме скорости жука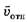 и линейной скорости точки
и линейной скорости точки 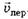 , в которой находится жук:
, в которой находится жук:
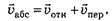

Скорость материальной точки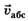 относительно неподвижной системы координат является векторной суммой скорости материальной точки относительно подвижной системы отсчёта
относительно неподвижной системы координат является векторной суммой скорости материальной точки относительно подвижной системы отсчёта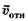 и скорости
и скорости 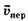 той части подвижной системы отсчёта относительно неподвижной, в которой в данный момент времени находится материальная точка.
той части подвижной системы отсчёта относительно неподвижной, в которой в данный момент времени находится материальная точка.
Отметим, что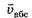 ,
,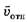 и
и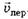 — это мгновенные скорости в рассматриваемый момент времени.
— это мгновенные скорости в рассматриваемый момент времени.
Модуль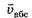 находится по теореме Пифагора:
находится по теореме Пифагора:
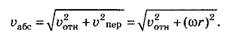
Угол φ между абсолютной и относительной скоростями можно определить из соотношения:
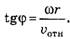
Относительно подвижной системы отсчёта, связанной с диском, жук движется прямолинейно и его траектория — отрезок АО. Относительно неподвижной системы отсчёта жук описывает криволинейную траекторию — спираль (см. рис. 2). Вектор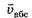 направлен по касательной к ней в точке А.
направлен по касательной к ней в точке А.
Рассмотрим ещё один пример. Пусть диск радиусом R вращается относительно неподвижной оси, проходящей через точку О, с постоянной угловой скоростью 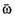 , а материальная точка А движется к нему вдоль линии АО с постоянной скоростью
, а материальная точка А движется к нему вдоль линии АО с постоянной скоростью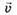 (рис. 3). В некоторый момент времени расстояние от края диска до точки А равно l. Определим скорость
(рис. 3). В некоторый момент времени расстояние от края диска до точки А равно l. Определим скорость 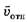 материальной точки в этот момент относительно вращающегося диска.
материальной точки в этот момент относительно вращающегося диска.
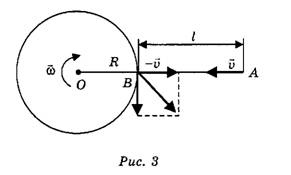
Скорость точки А относительно диска 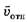 определяется её абсолютной скоростью
определяется её абсолютной скоростью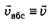 и переносной скоростью υпер = ω(ОА) = ω(R+l) (мгновенной скоростью той точки подвижной системы отсчёта, связанной с диском, где в данный момент времени находится материальная точка). Модуль скорости находится по теореме Пифагора
и переносной скоростью υпер = ω(ОА) = ω(R+l) (мгновенной скоростью той точки подвижной системы отсчёта, связанной с диском, где в данный момент времени находится материальная точка). Модуль скорости находится по теореме Пифагора
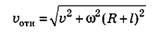
и угол
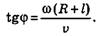
Таким образом, закон сложения скоростей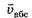 =
= 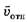 +
+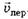 является обобщением закона сложения скоростей при поступательном движении подвижной системы отсчёта относительно неподвижной.
является обобщением закона сложения скоростей при поступательном движении подвижной системы отсчёта относительно неподвижной.
Отметим, что при поступательном движении переносная скорость является скоростью подвижной системы относительно неподвижной.
Обратите внимание на ещё одно существенное отличие поступательного движения системы отсчёта от непоступательного. В случае поступательного движения систем относительно друг друга
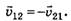
Это означает, что скорость первой материальной точки относительно второй 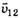 равна по модулю и противоположна по направлению скорости второй материальной точки -
равна по модулю и противоположна по направлению скорости второй материальной точки - 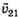 относительно первой.
относительно первой.
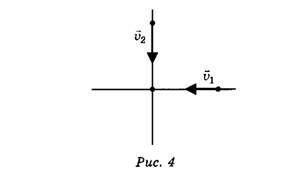
Например, если два автомобиля движутся поступательно со скоростями 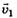 и
и 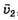 , как показано на рисунке 4, то
, как показано на рисунке 4, то 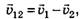 а
а 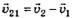 . Докажите это самостоятельно.
. Докажите это самостоятельно.
В случае непоступательного движения систем такое соотношение υ12 = -υ21 неверно!
В рассмотренном выше примере (см. рис. 3), если наблюдатель находится в точке В, то в системе отсчёта, связанной с точкой А, его скорость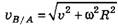 . А скорость точки А относительно системы отсчёта, связанной с точкой В,
. А скорость точки А относительно системы отсчёта, связанной с точкой В,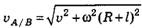
Как видно, скорость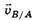 не совпадает со скоростью
не совпадает со скоростью 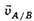 ни по модулю, ни по направлению. Модули скоростей υB/A<υA/B. Направление скорости
ни по модулю, ни по направлению. Модули скоростей υB/A<υA/B. Направление скорости 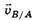 можно задать углом ос между ней и радиусом, проведённым в рассматриваемую точку. Тангенс этого угла (см. рис. 4) вычисляется как tg(α) = ωR/υ; направление скорости
можно задать углом ос между ней и радиусом, проведённым в рассматриваемую точку. Тангенс этого угла (см. рис. 4) вычисляется как tg(α) = ωR/υ; направление скорости 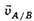 — углом β, который определится из соотношения tgβ=ω(R+l)/υ.
— углом β, который определится из соотношения tgβ=ω(R+l)/υ.
Приведём примеры решения задач с использованием закона сложения скоростей.
Задача 1. Два велосипедиста начинают одновременно движение с постоянными скоростями вдоль прямолинейного склона горы длиной l = 100 м: первый со скоростью υ1 = 4 м/с — поднимается вверх, а второй со скоростью υ2 = 6 м/с — спускается вниз. Найдите время tB и место хв встречи велосипедистов, если в начальный момент времени первый находился у основания склона, а второй — на его вершине.
Решение
Решим задачу в системе отсчёта, связанной с одним из велосипедистов, т. е. рассмотрим движение одного велосипедиста относительно другого. В этой системе отсчёта скорость сближения велосипедистов (относительная скорость) υ= υ1+υ2 .
Тогда время встречи определится из уравнения l = (υ1+υ2)tB.
Отсюда
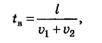
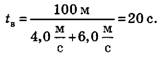
Место встречи определим из закона движения первого велосипедиста:
хв=υ1*tв
хв=4(м/с)*10(с) = 40 (м).
Ответ: tв = 10 c, хв = 40 м.
Задача 2. По двум пересекающимся под углом α =60° прямолинейным участкам дороги движутся с постоянными скоростями υ1 = 26 м/с и υ2 = 15 м/с два автомобиля (рис. 5).
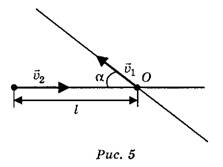
В некоторый момент времени первый автомобиль проезжает перекрёсток, в то время как второй движется к нему, находясь от него на расстоянии l = 500 м. Определите, через какой промежуток времени ∆t расстояние между автомобилями станет минимальным dmin, и найдите это минимальное расстояние.
Решение
При решении задач на закон сложения скоростей всегда приходится отвечать на следующие вопросы: с каким объектом связать неподвижную систему отсчёта К, а с каким — подвижную систему отсчёта К'? Что является движущейся материальной точкой? Наиболее простое решение получится, если неподвижную систему отсчёта К связать с первым автомобилем, пересекающим перекрёсток, подвижную К' — с землёй, а в качестве движущейся материальной точки взять второй автомобиль.
Тогда подвижная система отсчёта К', связанная с землёй, перемещается относительно неподвижной, связанной с первым автомобилем, со скоростью -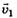 , т. е.
, т. е.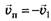 . Скорость второго автомобиля относительно земли является скоростью материальной точки относительно подвижной системы отсчёта
. Скорость второго автомобиля относительно земли является скоростью материальной точки относительно подвижной системы отсчёта 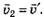 В результате скорость второго автомобиля относительно первого рассчитываем по формуле (рис. 6)
В результате скорость второго автомобиля относительно первого рассчитываем по формуле (рис. 6)
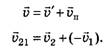
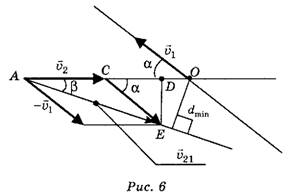
Что даёт такой выбор систем отсчёта? Первый автомобиль в ней неподвижен и находится в точке О, а второй движется относительно него с постоянной скоростью 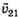 и, следовательно, наименьшее расстояние dmin между ними равно длине отрезка перпендикуляра, опущенного из точки О на отрезок АЕ, где
и, следовательно, наименьшее расстояние dmin между ними равно длине отрезка перпендикуляра, опущенного из точки О на отрезок АЕ, где 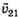 =
=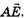
Из треугольников ∆AED и ∆CED находим:
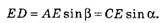
С учётом того, что AE = υ21, AC = υ1, получаем
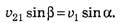
Отсюда находим
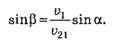
По теореме косинусов из ∆АСЕ находим
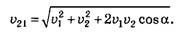
Из рисунка видно, что dmm = l*sinβ, тогда
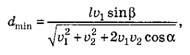
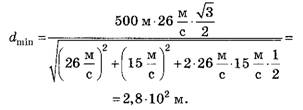
Теперь найдём
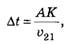
где АК = l*cosβ, а 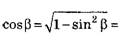
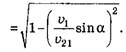
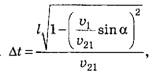
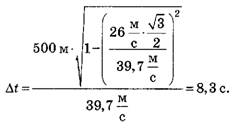
Ответ: dmin = 2,8*102 м, ∆t = 8,3с.
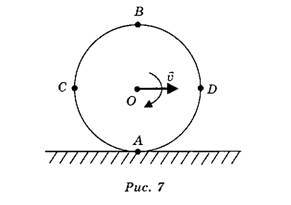
Задача 3. Колесо катится без проскальзывания с постоянной скоростью v по горизонтальному участку пути (рис. 7). Определите модули и направления скоростей точек А, В, С, D, лежащих на ободе колеса, относительно земли.
Решение
Свяжем подвижную систему отсчёта с центром катящегося колеса. По закону сложения скоростей скорость каждой точки колеса можно представить как векторную сумму скорости поступательного движения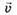 вместе с центром колеса и скорости вращения
вместе с центром колеса и скорости вращения 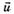 и вокруг этого центра (рис. 8).
и вокруг этого центра (рис. 8).
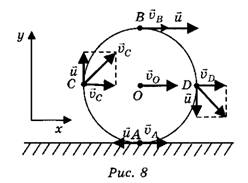
При этом следует помнить, что вектор линейной скорости движения по окружности у каждой точки имеет своё направление, поскольку он перпендикулярен радиусу, проведённому к рассматриваемой точке.
С учётом того, что u = ωr, в данном случае находим:
1) для точки А (поскольку движение происходит без проскальзывания, то она покоится относительно земли):
υA = υ-u = 0 => υ-u = ωr;
2) для точки В: υB = υ+u = υ+ υ = 2υ;
3) для точек С и D: согласно теореме Пифагора
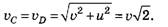
Направления соответствующих векторов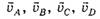 указаны на рисунке 8.
указаны на рисунке 8.
Поскольку точка А покоится относительно земли, то можно представить, что в течение малого промежутка времени колесо вращается относительно этой точки. Соответственно точка А называется мгновенным центром вращения, а все рассчитанные скорости могут быть найдены (убедитесь в этом самостоятельно) как линейные скорости движения по окружности вокруг точки А.
Ответ: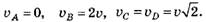
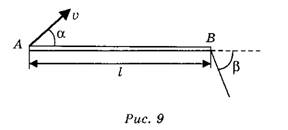
Задача 4. Палочка АВ длиной l движется в плоскости чертежа так, что в данный момент времени скорость её конца А направлена под углом α, а скорость конца В — под углом β к палочке (рис. 9). Модуль скорости точки А равен υ. Определите модуль скорости конца В палочки в данный момент. Найдите также положение мгновенной оси вращения палочки, т.е. положение неподвижной оси, перпендикулярной плоскости чертежа, относительно которой палочка вращается в данный момент времени.
Решение
Составляющая скорости вдоль палочки для всех точек палочки должна быть одинакова и равна u =υ*cos(α), поскольку в противном случае изменялась бы длина палочки.
Используя это условие, найдём скорость конца В палочки:
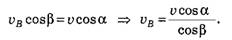
Согласно правилу сложения скоростей движение палочки можно рассматривать как совокупность поступательного движения вдоль АВ со скоростью u и вращательного движения вокруг оси, перпендикулярной плоскости чертежа и проходящей через некоторую точку О палочки.
Расстояние от точки О до конца палочки найдём из соотношения
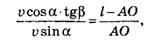
где
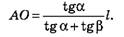
Соответственно движение палочки в данный момент времени можно рассматривать и как "чистое вращение" вокруг оси, проходящей через точку О', расположенную на перпендикуляре OO' к отрезку АВ.
Как следует из рисунка 10,
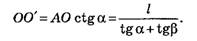
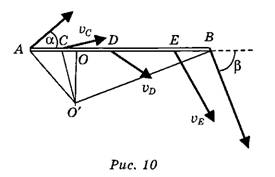
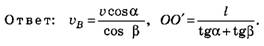
Задачи для самостоятельного решения
1. Лодка под парусом плывёт по ветру со скоростью υ=9,0(км/ч) относительно воды. Ветер относительно воды дует со скоростью u = 15 км/ч. Определите скорость ветра υв относительно лодки.
2. При равномерном движении двух тел навстречу друг другу расстояние между ними уменьшается на l1 = 16 м за каждые ∆t = 10 с. При движении этих же тел с прежними скоростями в одном направлении расстояние между ними увеличивается на l2=3,0м за каждые ∆t2 = 5,0 с. Определите скорость υ1 и υ2 каждого тела.
3. Пассажир поднимается по неподвижному эскалатору метрополитена за ∆t = 3 мин, а по движущемуся вверх — за ∆t2 = 2 мин. Сможет ли он подняться по эскалатору, движущемуся с такой же скоростью вниз? Если сможет, то за какое время?
4. Пролетая над пунктом А, пилот вертолёта догнал воздушный шар, который сносило ветром по курсу вертолёта. Через полчаса пилот повернул обратно и встретил воздушный шар на расстоянии l = 30 км от пункта А. Определите скорость ветра υв, если мощность двигателя вертолёта оставалась постоянной.
5. Определите время ∆t полёта самолёта между пунктами, находящимися на расстоянии l = 500 км, если скорость самолёта относительно воздуха υс = 100 (м/с), а скорость встречного ветра, направленного под углом α = 30° к прямой, соединяющей эти пункты. Во сколько раз k уменьшится время полёта, если этот ветер будет попутным и его скорость направлена под углом α = 30° к направлению движения? Под каким углом β к направлению движения должна быть направлена скорость самолёта в обоих случаях?
6. Шарик радиусом R катится со скоростью υ0 по двум рельсам, расположенным на расстоянии d = 2a друг от друга (рис. 11). Найдите модуль скорости υA точки А относительно рельсов.
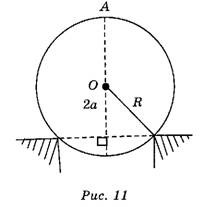
7. На горизонтальной поверхности стола лежит катушка, которая может катиться по столу без скольжения (рис. 12). На внутренний цилиндр катушки намотана нитка, конец которой тянут в горизонтальном направлении со скоростью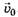 . Радиусы внешнего и внутреннего цилиндров равны соответственно R и r. Вычислите скорость и оси катушки.
. Радиусы внешнего и внутреннего цилиндров равны соответственно R и r. Вычислите скорость и оси катушки.
| Выложил | alsak |
| Опубликовано | 17.03.12 |
| Просмотров | 22166 |
| Рубрика | Решение задач |
| Тема | Кинематика |