Жидкевич В.И. Электрическое поле плоскости
Жидкевич В. И. Электрическое поле плоскости // Фізіка: праблемы выкладання. — 2009. — № 6. — С. 19—23.
Задачи по электростатике можно разделить на две группы: задачи о точечных зарядах и задачи о заряженных телах, размеры которых нельзя не учитывать [1—5].
Решение задач по расчёту электрических полей и взаимодействий точечных зарядов основано на применении закона Кулона и не вызывает особых затруднений. Более сложным является определение напряжённости поля и взаимодействия заряженных тел конечных размеров: сферы, цилиндра, плоскости. При вычислении напряжённости электростатических полей различной конфигурации следует подчеркнуть важность принципа суперпозиции и использовать его при рассмотрении полей, созданных не только точечными зарядами, но и зарядами, распределёнными по поверхности и объёму. При рассмотрении действия поля на заряд формула F=qE в общем случае справедлива для точечных заряженных тел и только в однородном поле применима для тел любых размеров и формы, несущих заряд q.
Электрическое поле конденсатора получается в результате наложения двух полей, созданных каждой пластиной.
В плоском конденсаторе можно рассматривать одну пластину как тело с зарядом q1 помещённое в электрическое поле напряжённостью Е2, созданное другой пластиной.
Рассмотрим несколько задач.
1. Бесконечная плоскость заряжена с поверхностной плотностью σ>0. Найдите напряжённость поля Е и потенциал ϕ по обе стороны плоскости, считая потенциал плоскости равным нулю. Постройте графики зависимостей Е(х), ϕ(х). Ось х перпендикулярна плоскости, точка х=0 лежит на плоскости.
Решение. Электрическое поле бесконечной плоскости является однородным и симметричным относительно плоскости. Его напряжённость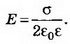 Связь между напряжённостью и разностью потенциалов между двумя точками однородного электростатического поля выражается формулой
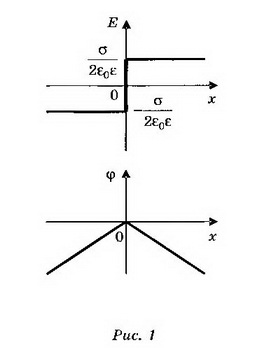
Связь между напряжённостью и разностью потенциалов между двумя точками однородного электростатического поля выражается формулой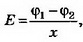 где х — расстояние между точками, измеренное вдоль силовой линии. Тогда ϕ2=ϕ1-Eх. При х<0
где х — расстояние между точками, измеренное вдоль силовой линии. Тогда ϕ2=ϕ1-Eх. При х<0 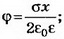 при х>0
при х>0 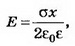
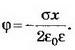 Зависимости Е(х) и ϕ(х) представлены на рисунке 1.
Зависимости Е(х) и ϕ(х) представлены на рисунке 1.
2. Две плоскопараллельные тонкие пластины, расположенные на малом расстоянии d друг от друга, равномерно заряжены зарядом поверхностной плотностью σ1 и σ2. Найдите напряжённости поля в точках, лежащих между пластинами и с внешней стороны. Постройте график зависимости напряжённости Е(х) и потенциала ϕ(х), считая ϕ(0)=0. Рассмотрите случаи, когда: a) σ1=-σ2; б) σ1= σ2; в) σ1=3σ2-
Решение. Так как расстояние между пластинами мало, то их можно рассматривать как бесконечные плоскости.
Напряжённость поля положительно заряженной плоскости равна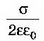 и направлена от неё; напряжённость поля отрицательно заряженной плоскости направлена к ней.
и направлена от неё; напряжённость поля отрицательно заряженной плоскости направлена к ней.
Согласно принципу суперпозиции поле в любой рассматриваемой точке будет создаваться каждым из зарядов в отдельности.
а) Поля двух плоскостей, заряженных равными и противоположными по знаку зарядами (плоский конденсатор), складываются в области между плоскостями и взаимно уничтожаются во внешних областях (рис. 2, а).
При х<0 Е=0, ϕ=0; при 0<x<d 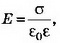
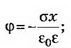 при x>d Е=0,
при x>d Е=0,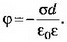 Графики зависимости напряжённости и потенциала от расстояния х приведены на рисунке 2, б, в.
Графики зависимости напряжённости и потенциала от расстояния х приведены на рисунке 2, б, в.
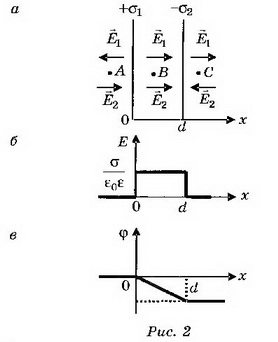
Если плоскости конечных размеров, то поле между плоскостями не будет строго однородным, а поле вне плоскостей не будет точно равно нулю.
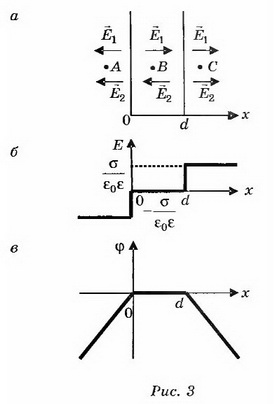
б) Поля плоскостей, заряженных равными по величине и знаку зарядами (σ1=σ2), компенсируют друг друга в пространстве между плоскостями и складываются во внешних областях (рис. 3, а). При х<0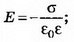 при 0<x<d E=0; при х>d
при 0<x<d E=0; при х>d 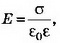
Воспользовавшись графиком Е(х) (рис. 3, б), построим качественно график зависимости ϕ(х) (рис. 3, в).
в) Если σ1= σ2, то, учитывая направления полей и выбирая направление направо за положительное, находим:
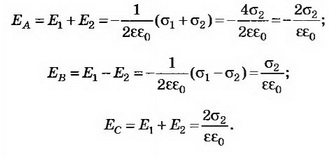
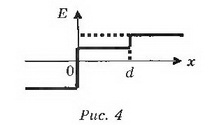
Зависимость напряжённости Е от расстояния показана на рисунке 4.
3. На одной из пластин плоского конденсатора ёмкостью С находится заряд q1=+3q, а на другой q2=+q. Определите разность потенциалов между пластинами конденсатора.
Решение. 1-й способ. Пусть площадь пластины конденсатора S, а расстояние между ними d. Поле внутри конденсатора однородное, поэтому разность потенциалов (напряжение) на конденсаторе можно определить по формуле U=E*d, где Е — напряжённость поля внутри конденсатора.
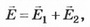
где Е1, Е2 — напряжённости поля, создаваемого пластинами конденсатора.
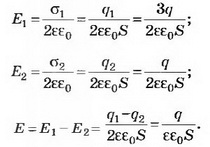
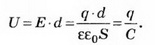
2-й способ. Добавим на каждую пластину заряд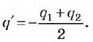 Тогда пластины конденсатора будут иметь заряды +q и -q. Поля одинаковых зарядов пластин внутри конденсатора компенсируют друг друга. Добавленные заряды не изменили поле между пластинами, а значит, и разность потенциалов на конденсаторе. U=q/C.
Тогда пластины конденсатора будут иметь заряды +q и -q. Поля одинаковых зарядов пластин внутри конденсатора компенсируют друг друга. Добавленные заряды не изменили поле между пластинами, а значит, и разность потенциалов на конденсаторе. U=q/C.
4. В пространство между обкладками незаряженного плоского конденсатора вносят тонкую металлическую пластину, имеющую заряд +q. Определите разность потенциалов между обкладками конденсатора.
Решение. Так как конденсатор не заряжен, то электрическое поле создаётся только пластиной, имеющей заряд q (рис. 5). Это поле однородное, симметричное относительно пластины, и его напряжённость 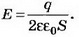 Пусть потенциал металлической пластины равен ϕ. Тогда потенциалы обкладок А и В конденсатора будут равны ϕ-ϕА=ϕEl1; ϕА=ϕ-El1; ϕ-ϕB=ϕ-El2; ϕB=ϕ-El2.
Пусть потенциал металлической пластины равен ϕ. Тогда потенциалы обкладок А и В конденсатора будут равны ϕ-ϕА=ϕEl1; ϕА=ϕ-El1; ϕ-ϕB=ϕ-El2; ϕB=ϕ-El2.
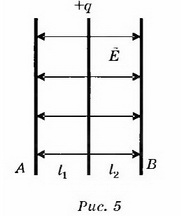
Разность потенциалов между обкладками конденсатора 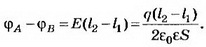 Если пластина находится на одинаковом расстоянии от обкладок конденсатора, то разность потенциалов между обкладками равна нулю.
Если пластина находится на одинаковом расстоянии от обкладок конденсатора, то разность потенциалов между обкладками равна нулю.
5. В однородное электрическое поле напряжённостью Е0 перпендикулярно силовым линиям помещают заряженную металлическую пластину с плотностью заряда на поверхности каждой стороны пластины σ (рис. 6). Определите напряжённость поля Е' внутри и снаружи пластины и поверхностную плотность зарядов σ1и σ2, которая возникнет на левой и правой сторонах пластины.
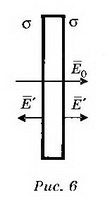
Решение. Поле внутри пластины равно нулю и является суперпозицией трёх полей: внешнего поля Е0, поля, создаваемого зарядами левой стороны пластины, и поля, создаваемого зарядами правой стороны пластины. Следовательно,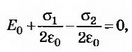 где σ1 и σ2 — поверхностная плотность заряда на левой и правой сторонах пластины, которая возникает после внесения пластины в поле Е0. Суммарный заряд пластины не изменится, поэтому σ1+σ2=2σ, откуда σ1=σ-ε0E0, σ2=σ+ε0E0. Поле снаружи пластины является суперпозицией поля Е0 и поля заряженной пластины Е. Слева от пластины
где σ1 и σ2 — поверхностная плотность заряда на левой и правой сторонах пластины, которая возникает после внесения пластины в поле Е0. Суммарный заряд пластины не изменится, поэтому σ1+σ2=2σ, откуда σ1=σ-ε0E0, σ2=σ+ε0E0. Поле снаружи пластины является суперпозицией поля Е0 и поля заряженной пластины Е. Слева от пластины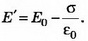 Справа от пластины
Справа от пластины 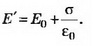
6. В плоском воздушном конденсаторе напряжённость поля Е= 104 В/м. Расстояние между обкладками d=2 см. Чему будет равна разность потенциалов, если между пластинами параллельно им поместить металлический лист толщиной d0=0,5 см (рис. 7)?
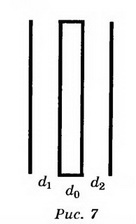
Решение. Поскольку электрическое поле между пластинами однородное, то U=Ed, U=200 В.
Если между пластинами пометить металлический лист, то получается система из двух последовательно соединённых конденсаторов с расстоянием между пластинами d1 и d2. Ёмкости этих конденсаторов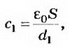
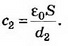 Их общая ёмкость
Их общая ёмкость
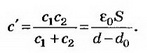
Так как конденсатор отключён от источника тока, то заряд конденсатора при внесении металлического листа не меняется: q'=CU=С'U1;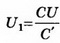 где
где 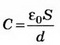 емкость конденсатора до внесения в него металлического листа. Получаем:
емкость конденсатора до внесения в него металлического листа. Получаем:
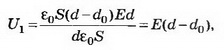
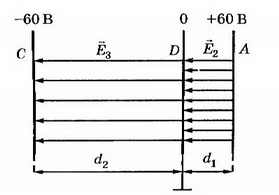
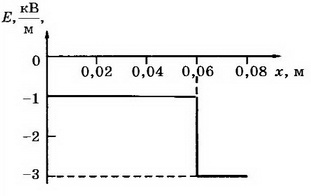
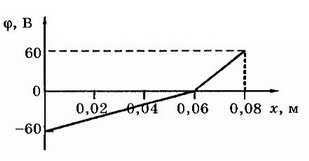
7. На пластинах А и С, расположенных параллельно на расстоянии d=8 см друг от друга, поддерживаются потенциалы ϕ1= 60 В и ϕ2=-60 В соответственно. Между ними поместили заземлённую пластину D на расстоянии d1=2 см от пластины А. На сколько изменилась напряжённость поля на участках AD и CD? Постройте графики зависимостей ϕ(x) и Е(х).
Решение. Первоначальная напряжённость поля между пластинами А и С:
E1=1,5 кВ/м.
Напряжённость поля на участке AD: Е2= ϕ1/d1, Е2=3 кВ/м, т. е. увеличилась на 1,5 кВ/м. Напряжённость поля на участке CD Е3= ϕ2/d2, т.е. уменьшилась на Е3=0,5 кВ/м. Поскольку векторы  направлены противоположно положительному направлению оси Ох, то Ег, Е2, Е3<0 (рис. 8).
направлены противоположно положительному направлению оси Ох, то Ег, Е2, Е3<0 (рис. 8).
8. Точечный заряд q=5*10-9 Кл находится на расстоянии 3 см от проводящей заземлённой стенки. Найдите поверхностную плотность заряда, индуцированного на стенке в точке А, ближайшей к заряду, и в точке В, находящейся на расстоянии 5 см от заряда.
Решение. В точках А, В, расположенных в непосредственной близости к поверхности проводника (рис. 9), поле создаётся точечным зарядом q и зарядом q', индуцированным на стенке: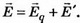
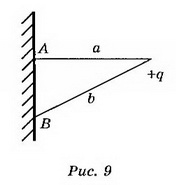
В точке А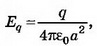 где а — расстояние от заряда до стенки,
где а — расстояние от заряда до стенки,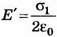 . Но поле внутри проводника равно нулю; следовательно,
. Но поле внутри проводника равно нулю; следовательно,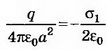 . Отсюда
. Отсюда 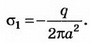
В точке В величина нормальной составляющей напряжённости поля точечного заряда
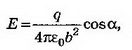
где b — расстояние от заряда до точки, cosα=a/b,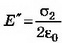 — напряжённость поля плоскости.
— напряжённость поля плоскости.
Следовательно,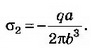
Список использованной литературы
1. Балаш, В. А. Задачи по физике и методы их решения / В. А. Балаш. — 4-е изд. — М. : Просвещение, 1983. — 432 с.
2. Бутиков, Е. И. Физика в примерах и задачах / Е. И. Бутиков, А. А. Быков, А. С. Кондратьев. — 3-е изд. — М. : Наука, 1989. — 462 с.
3. Зилъберман, Г. Е. Электричество и магнетизм / Г. Е. Зильберман. — М. : Наука, 1990. — 384 с.
4. Меледин, Г. В. Физика в задачах / Г. В. Меледин. — 2-е изд. — М. : Наука, 1990. — 270 с.
5. Сборник задач по физике / Л. П. Баканина [и др.]; под ред. С. М. Козела. — М. : Наука, 1990. — 347 с.
| Выложил | alsak |
| Опубликовано | 22.03.12 |
| Просмотров | 45829 |
| Рубрика | Решение задач |
| Тема | Электростатика |