Шепелевич В.В. Задача о радуге
Шепелевич В.В. Задача о радуге // Фізіка: праблемы выкладання. — 2009. — №6. — С. 26—36.
ЭСТЕТИЧЕСКОЕ И ХУДОЖЕСТВЕННОЕ ВОСПРИЯТИЕ РАДУГИ
Радуга — изумительное явление природы, всегда восхищающее, словно в первый раз. Можно предположить, что именно наблюдение радуги и сопровождающие его эмоции направляют естественное любопытство ребёнка на разгадку этого явления. Нередко это приводит к формированию устойчивого интереса к физике, которая способна полностью объяснить все детали этого явления.
На рисунке 1 изображён огромный мост из радуги, переброшенный через великую полесскую реку Припять. На рисунке 2 радуга начинает свой путь из великолепного деревянного средневекового Мозырского замка (единственного в Беларуси), воссозданного недавно по историческим описаниям и рисункам.
Под впечатлением этих чудесных картин невольно рождаются поэтические строки:
Над поймой Припяти широкой
Несётся с громом летний дождь,
А ты смиренно, одиноко
В своём укрытье солнца ждёшь.
И чудо летнее свершилось: Внезапно, солнцем рождено,
Виденье радуги явилось,
И освятило вдруг оно
Прекрасный вид из стен и башен,
Что украшают древний град.
Под нимбом радуги не страшен
Стихий разнузданных возврат.
Явление радуги отражено в эпосе древних народов, в стихах, песнях, легендах и преданиях. Можно предположить, что это слово произошло от названия бога солнца Ра. В [1] высказывается мнение, что слово "радуга" произошло от старославянского "радь", что означает "весёлый". Неслучайно в белорусском языке радугу называют "вясёлка".
О радуге придумано очень много загадок. Например: "Раскрашенное коромысло через реку повисло", "Раскинулся разноцветный мост на семь сёл, на семь вёрст", "Поднялись цветные врата — всему миру красота".


Радуга всегда считалась добрым предзнаменованием. Недаром в знаменитом "Дон Жуане" Дж. Байрона встречаются такие строки
...когда страданьем
Измучен ум, — приятно допустить,
Что радуга спасеньем может быть.
Наблюдение радуги поэты обычно ассоциировали с оптимистическим подходом к философской оценке жизни. Например, выдающийся немецкий поэт И. Гёте писал о радуге, наблюдаемой в брызгах водопада:
Всю нашу жизнь она воспроизводит:
Всмотрись в неё — и ты поймёшь душою,
Что жизнь на отблеск красочный походит.
Русский поэт Ф. И. Тютчев в непостоянстве и быстротечности явления радуги усматривает напоминание о скоротечности человеческой жизни:
Как неожиданно и ярко
На влажной неба синеве
Воздушная воздвиглась арка
В своём минутном торжестве!
Один конец в леса вонзила,
Другим за облака ушла —
Она полнеба обхватила
И в высоте изнемогла.
О, в этом радужном виденье
Какая нега для очей! Оно дано нам на мгновенье,
Лови его — лови скорей!
Смотри — оно уж побледнело, —
Ещё минута, две — и что ж?
Ушло, как то уйдёт всецело,
Чем ты и дышишь, и живёшь.
М. Ю. Лермонтов во второй части поэмы "Измаил-Бей" так описывает чудное явление радуги на Кавказе:
...Там разноцветною дугой,
Развеселясь, нередко дивы
На тучах строят мост красивый,
Чтоб от одной скалы к другой
Пройти воздушною тропой...
Не обошли стороной великолепие радуги и белорусские поэты. Например, Пимен Панченко в своём раннем стихотворении "Яблыня" (1936) пишет:
І ападаў на сад са звонам
Бліскучых буйных кропель рой...
А з поўдня ехаў май зялёны
Да нас з вясёлкавай дугой.
Анатоль Астрейко воспевает очищающую силу радуги в стихотворении "Вясна! У яркай квецеш..." (1961):
Вясёлка прамяністая
Згінаецца ў дугу,
Вадой змывае чыстаю
3імовую смугу.
Как формируются цветовые дуги радуги? Почему летом радугу нельзя наблюдать в наших широтах в полдень? Можно ли моделировать радугу с помощью компьютера? Эти и многие другие вопросы, касающиеся радуги, позволяют рассматривать данное физическое явление как перспективный объект для исследовательской работы учащихся, как сложную и многогранную исследовательскую задачу.
Прежде чем приступить к расшифровке загадки радуги, обратимся к истории развития физической теории радуги.
ИСТОРИЯ РАЗВИТИЯ ТЕОРИИ РАДУГИ
Впервые попытался объяснить явление радуги греческий философ и учёный Аристотель (384 -322 до н. э.). Он считал, что солнечные лучи, отражаясь необычным образом от дождевого облака, образуют конус радужных лучей [2].
Угол между падающим световым лучом и направлением от глаза наблюдателя на радугу был впервые измерен Робертом Бэконом в 1266 году. Было установлено, что он составляет примерно 42°.
В 1304 году немецкий монах Теодорик (см. обзор [2]) отошёл от аристотелевой гипотезы о коллективном отражении света дождевыми каплями и предположил, что каждая капелька по отдельности может создать радугу. Он подтвердил свою гипотезу экспериментальным созданием модели радуги при отражении света от сферической стеклянной колбы с водой.
В 1611 году Марк Антоний де Доминис (см., например, [3]) представил физическую картину формирования радуги при отражении и двукратном преломлении света в капле воды. Более полное объяснение явления радуги в 1635 году дал французский философ, математик, физик и физиолог Рене Декарт в главе "О радуге" своего труда "Метеоры" [4]. Методами геометрической оптики Декарт объяснил механизм образования первичной и вторичной радуг, а также распределение интенсивности света при формировании радуги. Исаак Ньютон в "Лекциях по оптике" [5] дополняет теорию радуги Декарта рассуждениями об образовании цветов радуги (см. также [6]).
Теория радуги с учётом дифракции света была построена лишь в XIX веке Дж. Б. Эйри (1836) и Дж. М. Пернтером (1897).
Уже в XX веке были установлены аналогии между столкновениями частиц и оптическими эффектами. Как и в оптике, рассеяние атомов газа друг на друге можно изучать, рассматривая их траектории как функцию прицельного параметра. Оказывается, при этом можно обнаружить явление, эквивалентное радуге. Впервые атомная "радуга" наблюдалась в 1964 году сотрудниками Боннского университета Хундхаузеном и Паули, которые изучали рассеяние атомов натрия на ртути. Подобные эксперименты выполнены уже и для рассеяния атомных ядер [2].
В настоящее время разработаны специальные математические методы, позволяющие создать количественную теорию, достаточно успешно описывающую формирование радуги с учётом дифракции света на дождевых каплях (см., например, [2]).
Проблемы теории радуги и её моделирования рассматриваются также в [7—12].
РЕШЕНИЕ ЗАДАЧИ О РАДУГЕ. ПЕРВИЧНАЯ РАДУГА
Для того чтобы понять, как формируется основная, или первичная, радуга, рассмотрим сначала ход световых лучей в капле воды.
Пусть на каплю воды в форме шара падает однородный световой поток. Предположим, что световые лучи в этом потоке параллельны друг другу. Рассмотрим сечение потока плоскостью, проходящей через центр капли. Для определённости сначала рассмотрим взаимодействие с каплей одного произвольно взятого монохроматического луча, находящегося на расстоянии р от прямой, проходящей через центр капли параллельно световым лучам (рис. 3).
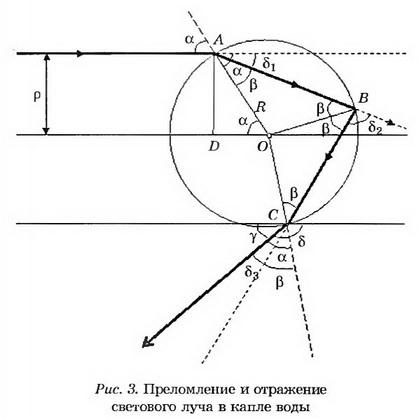
Величину ρ называют прицельным расстоянием. В точке А световой луч, падающий на поверхность капли под углом а, называемым углом падения, преломляется и распространяется внутри капли по прямой АВ. Преломлённый луч образует с радиусом OA угол β, называемый углом преломления. Достигая поверхности капли в точке В, луч АВ отражается. Угол отражения OBC равен углу падения ABO луча АВ. Но ABO=β, так как ∆АОВ равнобедренный, поэтому OBC также равен β. Отражённый в точке В луч доходит до точки С и преломляется на границе вода—воздух. Известно, что в оптике выполняется принцип обратимости световых лучей. Это значит, что если обратить луч АВ, т. е. направить его из точки В в точку А под углом β к поверхности капли, то он выйдет из капли под углом а к её поверхности. Эти же рассуждения можно применить к точке С, в которую луч ВС также падает под углом β. Поэтому луч ВС выйдет из капли под углом α.
Числовое значение прицельного параметра р зависит от выбора единиц измерения длины. Чтобы обойти связанные с этим проблемы, вводят безразмерную величину

называемую прицельным пара метром. Поскольку ρ может изменяться в пределах 0≤ρ≤R, величина прицельного параметра изменяется в пределах 0≤ξ≤1. Целью наших дальнейших расчётов будет определение угла ϒ, образованного вышедшим из капли световым лучом и прямой, проведённой из точки С в сторону источника света параллельно падающему лучу, как функции прицельного параметра ξ. Для этого сначала определим суммарное отклонение δ падающего луча от первоначального направления. Очевидно (см. рис. 3), оно определяется выражением
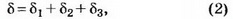
где δ1, δ2, δ3— отклонения светового луча в точках A, B и C соответственно. Величины δ1, δ2, δ3 будут выражаться через углы α и β.
Поэтому попытаемся выразить эти углы через прицельный параметр ξ.
Из прямоугольного треугольника ∆AOD получаем

Отсюда имеем

Угол β легко вычислить из закона преломления света
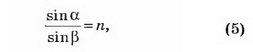
где n — относительный показатель преломления воды и воздуха. Если пренебречь отличием показателя преломления воздуха от 1, то в качестве n можно рассматривать показатель преломления воды.
Из формулы (5) можно выразить sin β
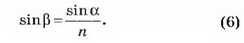
Подставим в (6) выражение (3). Получим

Угол β нетрудно выразить из (7):
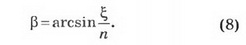
Используя рисунок 1, выразим угловые отклонения светового луча δ1, δ2, δ3 через прицельный параметр ξ. Получим
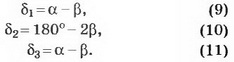
Подставляя выражения (9) — (11) в равенство (2) и учитывая формулы (4) и (8), будем иметь
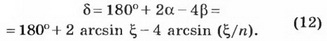
Из рисунка 1 видно, что полное отклонение светового луча δ связано с искомым углом ϒ соотношением

Подставляя выражение (12) в равенство (13), получаем
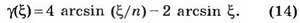
Формула (14) позволяет вычислить для каждого значения прицельного параметра ξ падающего на каплю светового луча угол ϒ, образованный выходящим после взаимодействия с каплей световым лучом с направлением вектора, проведённого из центра капли к солнцу.
Исследуем функцию ϒ(ξ) на экстремум. Для применения необходимого условия существования экстремума следует вычислить производную функции ϒ(ξ) по переменной ξ и приравнять её к нулю:
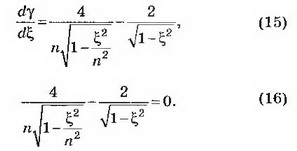
После переноса второго слагаемого в (16) в правую часть, возведения обеих частей равенства в квадрат и небольших преобразований получаем уравнение

решение которого даёт выражение прицельного расстояния, при котором достигается экстремум,
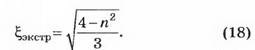
Поскольку показатель преломления воды обладает дисперсией, т. е. зависит от длины световой волны (цвета), следует выбрать для дальнейших расчётов определённый цвет. Обычно рассматривают взаимодействие с каплей жёлтых лучей, так как они находятся в солнечном спектре почти посередине видимого диапазона. Примем показатель преломления воды для жёлтого света

Тогда, подставляя (19) в (18), будем иметь
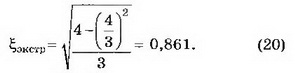
Применяя достаточное условие существования экстремума, легко убедиться, что при ξэкстр=0,861 достигается максимум функции ϒ(ξ). Подставляя ξ=0,861 в выражение (14), получаем, что ϒмакс~ 42,03°. Отсюда следует, что все световые лучи, выходящие из капли после преломлений и отражения, распространяются внутри конуса, образующие которого составляют угол 42,03° с осью, параллельной световым лучам и проходящей через центр капли.
С помощью системы компьютерной математики Маткад (MathCad) построим график функции ϒ(ξ) (рис. 4).
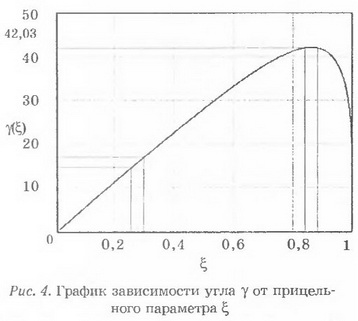
Из графика видно, что, как и предсказывалось выше, выходящие из капли световые лучи заполняют конус с углом раствора образующих 2ϒмакс=84,06°. За пределы этого конуса свет, отбрасываемый дождевыми каплями, не выходит. Поэтому область пространства за пределами рассмотренного конуса не освещена. Этот факт хорошо иллюстрируется моделью капли в виде стеклянной колбы с водой (рис. 5), предложенной и использованной Теодориком.
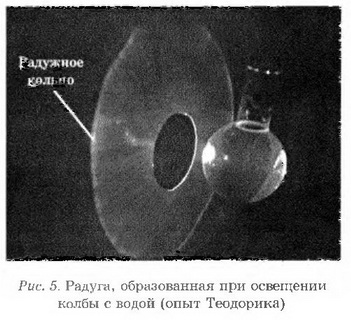
Свет от проекционного фонаря падает на тонкостенную сферическую колбу с водой через отверстие в картонном экране, диаметр которого равен диаметру колбы. Выходящие из колбы световые лучи освещают внутренность конуса с углом раствора образующих около 84°. При этом некоторым смещением световых лучей при их преломлении в стекле колбы пренебрегаем за счёт её тонкостенности. Хорошо видно, что за пределами указанного конуса экран не освещён.
Как же объяснить тот факт, что в опыте со стеклянной колбой с водой радужная окраска появляется только при углах ϒ, близких к максимальному значению этого угла? Подобная ситуация имеет место и при взаимодействии солнечного света с каплей воды. Для этого изучим график, изображённый на рисунке 4, более детально.
Рассмотрим два световых луча, таких, что их прицельные параметры заключены в пределах 0,2<ξ<0,4 и отличаются друг от друга на величину ∆=0,05. Из графика видно, что таким лучам соответствуют углы у, отличающиеся приблизительно на 2,5°.
Если же рассмотреть два луча с прицельными параметрами, близкими ξэкстр=0,861 и отличающимися на ту же величину ∆, то соответствующие им углы практически совпадают. Это означает, что вблизи края освещённого конуса (вблизи ϒмакс) световые лучи "сгущаются", т. е. интенсивность их становится большей, причём для лучей различного цвета значение ϒмакс также различно из-за дисперсии (зависимости показателя преломления п от длины световой волны). Поэтому внутри конуса все цвета, из которых состоит солнечный свет, не "сгущены" и при наложении снова образуют белый свет, а на краю конусов, построенных для каждого цвета, отдельные цвета "сгущаются", причём в таких узких областях, что практически не смешиваются друг с другом. Этим объясняется радужная окружность, наблюдаемая в опыте со стеклянной колбой с водой (см. рис. 5).
При расчёте углов ϒмакс для лучей различного света учтём, что для красного цвета nк=1,331, а для фиолетового — nф=1,344. Подставляя эти значения показателя преломления в формулу (18), находим значения прицельного параметра, соответствующие максимуму кривой ϒ(ξ) на рисунке 4: (ξк)экстр=0,862, (ξф)экстр=0,855. Определим с помощью этих значений прицельного параметра ϒмакс для красного и фиолетового цвета соответствующие углы максимального отклонения световых лучей по формуле (14): (ϒк)макс= 42,37°, (ϒф)макс= 40,51°. Полученные значения углов максимального отклонения красных и фиолетовых лучей показывают, что красный цвет удалён от центра радужной окружности дальше, чем фиолетовый.
Перейдём теперь к объяснению реальной радуги, которую видит наблюдатель, стоящий спиной к солнцу, а лицом — к завесе дождя, состоящей из системы водяных капелек, непрерывно падающих вниз. Капелька А, находящаяся в плоскости, проведённой через глаз наблюдателя, солнце и вертикальную прямую, проходящую через глаз наблюдателя, в некоторый момент оказывается в таком положении по отношению к наблюдателю, что один из цветных лучей, "сгущённых" у края конуса, попадает наблюдателю в глаз, формируя часть цветной дуги радуги (рис. 6).
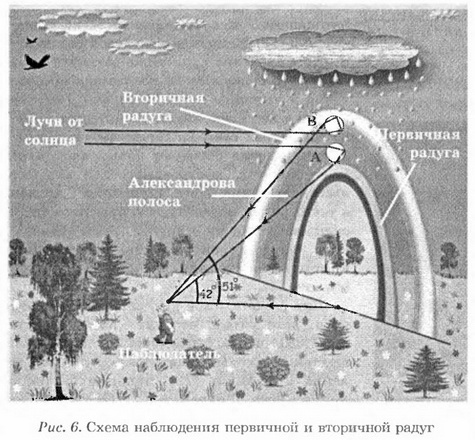
Световые лучи других цветов попадают в глаз наблюдателя от соседних капель. Свет, рассеянный каплями, находящимися выше цветной дуги радуги, вообще не попадает в глаз наблюдателя (тёмная Александрова полоса).
Отметим, что при наблюдении верхней точки дуги радуги в глаз наблюдателя приходят лучи, идущие от нижней части конуса "сгущения" световых лучей, идущих от отдельной капли дождя. В силу симметрии картины капель дождя по отношению к направлению оси, проходящей через центр солнца и глаз наблюдателя, радуга имеет вид окружности с центром, лежащим на оси, проходящей через солнце и глаз наблюдателя. Такую окружность можно наблюдать при созерцании радуги с самолёта. Тем не менее в обычных условиях нам не удаётся наблюдать её полностью, так как большая её часть "прячется" под землёй. Для лучшего понимания этого факта полезно использовать модель, иллюстрирующую положение радуги по отношению к земной поверхности. Эта модель (рис. 7) была разработана автором и изготовлена студентом V курса Мозырского государственного педагогического университета (2003 г.) Александром Бобером. Белый шар, закреплённый на металлическом стержне, моделирует солнце. Круг с вырезанным сектором моделирует земную поверхность. Точка расположения шарнирного соединения стержня с плоскостью круга моделирует наблюдателя. В случае, когда радуга наблюдается при заходящем солнце (рис. 7, а), видна половина радужного круга. Другая половина "прячется" под плоскостью горизонта. Случай, когда солнце находится под углом, меньшим чем 42°, моделируется на рисунке 7, б. Из рисунка 7, в видно, что при высоте солнца над горизонтом, превышающей 42°, радуга не может быть видна, так как образуемый ею конус полностью "спрятан" под землёй. В этом случае радугу можно увидеть только с самолёта, с высокой вышки или с края обрыва.



Рис. 7. Модель, наглядно демонстрирующая взаимное расположение солнца, наблюдателя, конуса радуги и плоскости горизонта:
а — радуга на закате солнца; б — радуга после полудня; в — невидимая "радуга" в полдень
ВТОРИЧНАЯ РАДУГА
Рассмотрим теперь физическое объяснение возникновения вторичной радуги (см. рис. 6, преломление в капле В). Учтём отражение светового луча в точке С на рисунке 3. Отражённый в этой точке луч CD выйдет из капли в точке D (рис. 8).
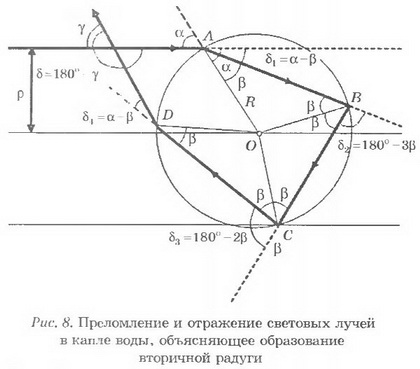
Определим угол ϒ1, образованный вышедшим из капли лучом с плоскостью горизонта. Для этого рассмотрим отклонение падающего на каплю светового луча после его преломления в точке А, отражения в точках В и С и преломления в точке D.
Из рисунка 8 видно, что суммарное отклонение светового луча 5 складывается из четырёх отклонений луча δA, δB, δC и δD в точках А, В, С и D соответственно, причём
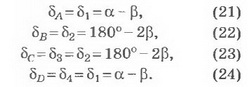
Тогда
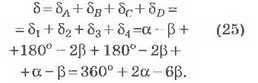
Легко увидеть, что
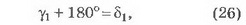
Подставляя в (26) выражение (25), получаем
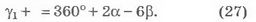
Отсюда имеем
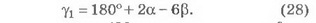
Подставляя в (28) выражения а и р из (4) и (8), получаем
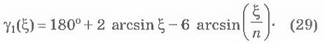
Построим с помощью MathCad график функции ϒ1(ξ) (29) вместе с графиком функции ϒ(ξ) (14) (рис. 9):
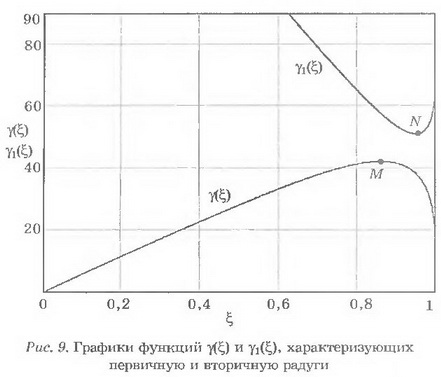
Функция ϒ1(ξ), как и функция имеет область определения 0≤ξ≤1 и принимает в точке ξ=0 значение 180°, т. е. определяет некоторое осветление неба за спиной наблюдателя. Однако яркость такого осветления резко падает с увеличением угла ϒ1. Поэтому на рисунке 9 рассмотрены только значения ϒ1 лежащие в интервале от (ϒ1)миним до 90°.
Из рисунка 9 хорошо видно, что точки М и N экстремумов функций ϒ1(ξ) и ϒ(ξ) достигаются при различных прицельных параметрах ξ. Процедуру аналитического определения координат точки N, аналогичную процедуре определения координат точки М, выполненной выше, предлагаем читателю провести самостоятельно. Для жёлтого цвета (n=4/3) должны получиться значения, согласованные с построенным на рисунке 9 графиком: ξэкстр=0,95, (ϒ1)миним=50,98°.
Объяснение возникновения вторичной радуги, так же как и первичной, связано со "сгущением" световых лучей, имеющим место вблизи (ϒ1)миним=50,98".
Из рисунка 9 можно также определить ширину тёмной Александровой полосы, заключённой между ϒмакс и (ϒ1)миним Легко также проверить, что чередование цветов во вторичной радуге противоположно их чередованию в первичной радуге, т. е. красный цвет во вторичной радуге располагается снизу, а фиолетовый — сверху (см. также рис. 6).
В литературе описано множество модельных экспериментов, связанных с явлением радуги. В частности, в [12] предлагаются эксперименты по наблюдению первичной и вторичной радуг с использованием цилиндра из плексигласа или мензурки с водой. В статье [10] описан метод получения искусственной радуги на металлической пластинке, покрытой сажей. Результат реализации этого метода, полученный студентами Мозырского государственного педагогического университета имени И. П. Шемякина, представлен на рисунке 10.

ПОЛЯРИЗАЦИЯ РАДУГИ
Рассмотрим ещё одно удивительное физическое свойство радуги: поляризацию исходящего от неё света. Оказывается, при наблюдении радуги через обычную поляроид-ную плёнку при определённой ориентации плёнки можно сделать радугу почти полностью невидимой, тогда как тучи на небе будут хорошо видны. Это означает, что свет, идущий от радуги, почти полностью поляризован.
Хотя поляризация света изучается в школьном курсе физики весьма поверхностно, возможность экспериментального наблюдения поляризованного света радуги и не очень сложный математический аппарат, необходимый для объяснения её поляризационных свойств, искушают попробовать объяснить поляризацию света радуги. Единственным дополнительным законом, не изучаемым в школе, знание которого необходимо для понимания поляризации света радуги, является закон Брюстера. Этот закон можно сформулировать в следующей форме: "Если неполяризованный свет отражается от поверхности раздела двух сред с показателями преломления n1 и n2, причём свет падает из среды с показателем преломления n1 то при выполнении равенства

где ϕ0— угол падения, отражённый свет полностью поляризован перпендикулярно плоскости падения, т. е. вектор напряжённости электрического поля в отражённом свете колеблется перпендикулярно плоскости падения". При этом угол ϕ0 называют углом Брюстера.
Определим угол ϕ0 при отражении света в точке В внутри дождевой капли (см. рис. 3). Очевидно, он равен углу β. Но угол β для "сгущённых" лучей жёлтого цвета, образующих радугу, определяется выражением (8) с учётом равенства (20):
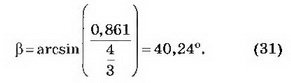
Из (30) следует, что для жёлтых лучей угол Брюстера ϕ0=36,87°, т. е. отличается от угла β, определяемого формулой (31) и характеризующего распространение "сгущённых" лучей, менее чем на 3°. Отсюда можно сделать вывод, что свет первичной радуги почти полностью поляризован в направлении касательной к дуге радуги. В этом действительно можно убедиться, наблюдая радугу через поляризатор.
При втором внутреннем отражении в точке С (см. рис. 8) свет поляризуется ещё в большей степени, причём также в направлении касательной к дуге вторичной радуги.
Итак, поляризация радуги в общих чертах объяснена. Более строгие вычисления
можно выполнить с помощью статьи [12].
* * *
Таким образом, мы рассмотрели физическое объяснение возникновения первичной и вторичной радуг, определили их количественные характеристики и сопоставили эти характеристики с результатами экспериментов. Кратко рассмотрена также поляризация света, идущего от радуги. Однако тему радуги ни в коем случае нельзя считать исчерпанной. Например, при рассмотрении хода лучей в капле не учитывались угловые размеры солнечного диска и вытекающее из этого некоторое отклонение от параллельности падающих на каплю лучей. Не объяснены причины появления периодически повторяющихся наборов цветных полос в нижней части дуги первичной радуги. При объяснении явления радуги мы не использовали размеров капель, которые, как показывает опыт, влияют на яркость цветов радуги и некоторые другие её характеристики.
Многие из перечисленных деталей явления радуги позволяет объяснить дифракционная теория взаимодействия световых волн с водяными каплями. Однако эта теория очень сложна и здесь рассматриваться не будет. Некоторые полезные сведения о результатах применения этой теории можно найти в обзоре [2] и в книге [7].
Список использованной литературы
1. Тарасов, Л. В. Физика в природе: кн. для учащихся / Л. В. Тарасов. — М. : Просвещение, 1988. — 351 с.
2. Нуссенцвейг, X. Теория радуги / X. Нуссенцвейг // УФН. — 1978. — Т. 125. — С. 527 — 547.
3. Трифонов, В. Д. Ещё раз о радуге / В. Д. Трифонов // Соросовский образовательный журнал. — 2000. — Т. 6, № 7. — С 53—58.
4. Декарт, Р. Рассуждения о методе (с приложениями Диоптрика, Метеоры, Геометрия) / Р. Декарт. — М. : Изд-во АН СССР, 1953. — 656 с.
5. Ньютон, И. Лекции по оптике / И. Ньютон. — М. : Изд-во АН СССР, 1945. — 280 с.
6. Брэгг, У. Мир света. Мир звука / У. Брэгг. — М. : Наука, 1967. — 336 с.
7. Миннарт, М. Свет и цвет в природе / М. Миннарт. — М. : Наука, 1969. — 344 с.
8. Булат, В. Л. Оптические явления в природе / В. Л. Булат. — М. : Просвещение, 1974. — 143 с.
9. Уокер. Дж. Физический фейерверк / Дж. Уокер. — М. : Мир, 1979. — С. 120—122.
10. Майер, В. Искусственная радуга / В. Майер, Р. Майер // Квант. — 1988. — № 6. — С. 48—50.
11. Гегузин, Я. Кто творит радугу? / Я. Гегузин // Квант. — 1988. — № 6. — С. 46—48.
12. Graham, G. R. Polarization of rainbows / G. R. Graham // Phys. Educ. — 1978. — V. 10, N 1. — C. 50—51.
| Выложил | |
| Опубликовано | 01.08.16 |
| Просмотров | 13507 |
| Рубрика | Решение задач |
| Тема | Оптика |