Кротов В.М. Многоуровневые задачи по физике
Кротов В.М. Многоуровневые задачи по физике // Фiзiка: праблемы выкладання. – 1997. – Вып. 7. – С. 88-90.
Вполне понятно, что овладение учащимися способами решения задач — одна из важнейших целей обучения физике. Для этого необходимым является создание многих условий, среди которых — высокий уровень мотивации деятельности, соответствующая теоретическая подготовка, учет индивидуальных способностей учащихся, подбор задач, обеспечивающих динамику усложнения деятельности.
Один из путей создания перечисленных условий — использование в обучении многоуровневых задач. Под многоуровневыми задачами мы понимаем те, в которых описывается конкретная ситуация и сформулированы несколько требований в определенном порядке. Каждое последующее требование «сложнее» предыдущих и может быть успешно реализовано при выполнении всех предыдущих.
Приведем несколько примеров таких задач.
I. Из точки А, находящейся на вершине крутого обрыва на высоте Н над горизонтом, бросают небольшой предмет в точку В горизонтальной поверхности, отстоящую на расстоянии L от обрыва.
1. Опишите возможные варианты бросков предмета в точку В.
2. С какой скоростью необходимо бросить предмет горизонтально, чтобы он упал в точку В?
3. Тело брошено горизонтально. С какой скоростью и под каким углом к горизонту упадет тело?
4. Бросание производят под углом α к горизонту. Какова взаимосвязь между uaи α?
5. При каком угле бросания aскорость предмета будет наименьшей?
6. Чему равна эта минимальная скорость броска?
II. Над идеальным газом проводят замкнутый цикл, изображенный в координатах p–T.
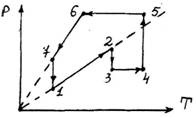
1. Какие процессы осуществляются на каждом из участков?
2. На каких участках газом совершается работа и на каких нет? На каких участках газ получает количество теплоты и на каких отдает?
3. Изобразите цикл в координатах Т–Vиобоснуйте его построение.
4. Изобразите цикл в координатах Т–р и обоснуйте его построение.
III. Плоский воздушный конденсатор с расстояниями между пластинами 3 см и площадью каждой из них 60 см2 присоединен к источнику постоянного напряжения 2000 В. Параллельно пластинам конденсатора вводится металлическая пластинка толщиной 1 см.
1. Определите первоначальную емкость конденсатора.
2. Определите электроемкость образовавшегося конденсатора.
3. Какой заряд протекает по цепи при введении металлической пластинки?
4. Какую энергию расходует источник при введении пластинки? На сколько при этом изменяется энергия конденсатора?
5. Пластинку вставляют в заряженный конденсатор, отключенный от источника. Изменится ли заряд конденсатора? Как изменится энергия конденсатора?
6. Какую работу совершает поле, если пластинку вставляют в заряженный конденсатор, отключенный от источника? Сравните ее с изменением энергии конденсатора.
IV. Две собирающие линзы с фокусным расстоянием 40 и 80 см установлены на расстоянии 20 см друг от друга так, что их главные оптические оси совпадают. Предмет помещен на расстоянии 60 см от первой линзы.
1. Построением установите, где будет находиться изображение предмета. Что будет происходить с изображением, если линзы сдвинуть, раздвинуть?
2. Теоретически рассчитайте местонахождение изображения предмета.
3. Определите линейное увеличение, которое создает система линз при заданных условиях.
4. Что изменится, если линзы поменять местами?
5. Где будет находиться изображение предмета, если все элементы системы поменять местами?
V. Рамка из провода сопротивлением 0,01 Ом равномерно вращается в однородном магнитном поле с индукцией 0,05 Тл. Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Площадь рамки 100 см2.
1. Определите направление индукционного тока в рамке в течение первого полупериода ее вращения.
2. Определите электрический заряд, который протекает через рамку за время ее поворота на угол от 0 до 30° (угол отсчитывается между направлением В и нормалью к плоскости рамки).
3. По какому закону изменяется ЭДС индукции?
4. Постройте график изменения индукционного тока от времени.
5. Чему численно равна площадь фигуры, ограниченной графиком и осью времени? Какой средний ток протекает в контуре за период? Полупериод?
Решение многоуровневых задач позволяет:
1) учесть индивидуальные способности учащихся (каждый учащийся выполняет столько требований, сколько может осилить);
2) больше времени отводить на анализ задачных ситуаций (нет необходимости решать большее количество задач);
3) решить проблему с подбором задач при обучении учащихся на разных уровнях (базовом, профильном, углубленном);
4) более четко организовать самостоятельную работу учащихся (выполнение отдельных требований предоставить самим учащимся, предложить по рассматриваемой заданной ситуации составить новые требования).
| Выложил | alsak |
| Опубликовано | 22.03.08 |
| Просмотров | 10380 |
| Рубрика | Методика | Решение задач |
| Тема | Без тем |