Акуленко В.Л. Ударные силы – школьная физика или теоретическая механика?
Кто-то из мудрых сказал замечательные слова: «Не страшись быть опровергнутым, страшись быть непонятым». Возможно, в контексте этого высказывания будет понятен мотив ответа на публикацию Е.Е. Волынца «Еще раз об «оптимальном угле», напечатанную в первом номере журнала за 2004 г.
Прежде всего хотелось бы поблагодарить автора данной статьи за то внимание, которое он уделил моей работе: любому автору приятно осознавать, что его работа так или иначе не осталась незамеченной.
Но вернемся к существу вопроса. В статьях «Классическая ошибка» и «Оптимальный угол» мною был предложен новый подход к решению задач, связанных с переходом тела от движения по наклонной плоскости к плоскости горизонтальной и наоборот. Ε. Ε. Волынец предлагает к тем же задачам свои решения, некоторым образом отличающиеся от решений, ранее предложенных мною.
Таким образом, сложилась спорная ситуация: в рамках одного издания предлагаются два различных подхода к решению одних и тех же задач, приводящих к различным ответам. Целью настоящей статьи является разрешение данного противоречия.
Позволю себе напомнить читателям постановку задачи и два подхода к ее решению – мой и Е.Е. Волынца.
Задача. Тело соскальзывает с плоскости с углом наклона α и продолжает скользить далее по горизонтальному участку. С какой скоростью u тело начнет движение по горизонтальному участку, если в момент времени, предшествующий удару тела о горизонтальную плоскость, тело имело скорость u0?
Решение В.Л. Акуленко. Так как при переходе на горизонтальный участок тело соударяется с горизонтальной плоскостью, то оно неизбежно передает земле часть импульса. Следует определить, какую именно часть импульса теряет тело при ударе.
Разложим импульс, которым обладает тело перед ударом, на горизонтальную ![]() и вертикальную
и вертикальную ![]() составляющие (рис. 1).
составляющие (рис. 1).
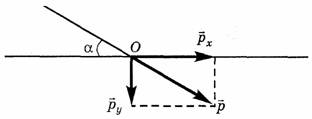
Рис. 1.
Очевидно, вертикальная составляющая ![]() в процессе соударения передается земле. Следовательно, движение по горизонтальной плоскости тело начнет за счет горизонтальной составляющей импульса
в процессе соударения передается земле. Следовательно, движение по горизонтальной плоскости тело начнет за счет горизонтальной составляющей импульса ![]() .
.
Как видно из рисунка 1, ![]()
![]() . Следовательно,
. Следовательно, ![]() .
.
Решение Е.Е. Волынца. В момент удара наиболее существенно влияние сил, изменяющих скорость движения. Таковыми являются сила трения и сила реакции опоры. Согласно второму закону Ньютона:
![]()
Найдя проекции этого уравнения на оси координат (рис. 2) и пренебрегая силой тяжести в момент удара, получим:
![]()
![]()
Разделив эти уравнения друг на друга, получим:
![]()
Из этого уравнения получим:
![]()
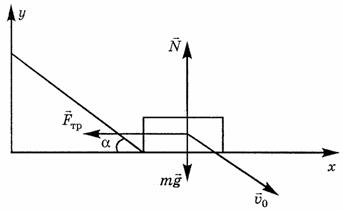
Рис. 2.
К сожалению, Е.Е. Волынец не обратил внимания на один из самых важных вопросов, разбираемых в моих работах, а именно – на необходимость проводить анализ полученного в ходе решения задач ответа. Очевидно, что если угол наклона плоскости α будет составлять с горизонтом 90°, тело не будет иметь никакой скорости, т.е. при α = 0° u = 0.
Подвергнем оба ответа такому анализу: если a = 0, то
![]() ;
;
![]()
Итак, ответ, полученный мною, выдерживает анализ; ответ же, полученный Е.Е. Волынцом, такого анализа не выдерживает.
Посмотрим, какую трактовку появлению отрицательного значения дает сам автор: «... если ![]() , тело остановится у основания наклонной плоскости».
, тело остановится у основания наклонной плоскости».
Совершенно непонятно, из чего следует это утверждение. На мой взгляд, если вдруг появляется отрицательный результат там, где он может быть только больше или равным нулю, можно сделать вывод о том, что при решении задачи не были учтены определенные аспекты. В данном случае автор упустил из виду то обстоятельство, что в рамках предлагаемого им подхода к решению задачи тело получает вращательный момент. Учесть же вращательный момент в рамках условия данной задачи практически невозможно, тем более это не по силам сделать школьникам, с которыми мы, собственно, и работаем.
Более того, Е.Е. Волынец незаметно переводит задачу из школьного курса физики в область теоретической механики, в которой изучаются ударные силы и связанные с ними явления.
Согласен, формально школьник может воспроизвести все шаги решения, учитывающего действие ударной силы трения, но для понимания и осознания этих действий ему понадобятся знания из области теории пределов. Вкратце поясню, что я имею в виду.
Итак, какая сила изменяет горизонтальную составляющую скорости тела в процессе удара? Это сила трения. Но сила трения, как и любая другая сила, может совершить работу только при условии, что телом будет пройден некоторый путь. Как объяснить школьнику, что нечто очень большое (ударная сила трения), будучи умноженным на нечто очень маленькое (путь тела по горизонтальному участку), дает определенный конечный результат?
Подведем итог: решение, предложенное Е.Е. Волынцом, бесспорно, усложнено, ответ же не безукоризненный.
Еще хотелось бы обратить внимание на то, что в моей работе «Оптимальный угол» присутствует ссылка на мою же статью «Классическая ошибка», где в свою очередь отмечается, что переход тела от движения по наклонной плоскости к движению по плоскости горизонтальной есть явление весьма сложное и модель, предлагаемая мною, является лишь определенной, оправданной в рамках школьного курса физики идеализацией реального физического процесса. Является ли таковой модель, предлагаемая Е.Е. Волынцом, предоставляю судить третьим лицам.
В любом случае, благодаря замечаниям Е.Е. Волынца в дальнейших своих публикациях на эту тему во избежание недоразумений условия своих задач на данную тему буду дополнять следующим указанием: «действием сил трения в момент удара тела о горизонтальную плоскость пренебречь».
Хочется еще раз отметить, что, решая физические задачи школьного курса, мы имеем дело не с реальными физическими процессами, а лишь с их математическими моделями, отражающими эти процессы в том или ином приближении. И, на мой взгляд, уместно остановиться на модели в том приближении, в котором она понятна школьникам.
И еще несколько слов о статье Е. Е. Волынца. В заключительной ее части автор рассматривает задачу об абсолютно упругом ударе тела о шероховатую поверхность. В процессе ее решения автор опять-таки не учитывает вращательного момента, получаемого телом при ударе о плоскость, и не делает соответствующей оговорки, без которой полученный им ответ лишен смысла. Заинтересовавшиеся данной темой читатели могут найти подробное решение задач такого типа в книге Е.И. Бутикова и др. «Физика в примерах и задачах».
| Выложил | alsak |
| Опубликовано | 12.08.13 |
| Просмотров | 6221 |
| Рубрика | Решение задач |
| Тема | Законы сохранения |