Кротов В.М. К вопросу о сложности физических задач
Во многих сборниках задач по физике содержатся задачи разной сложности (трудности). Выделяются простые, сложные и очень сложные задачи. Обозначенные уровни трудности по-разному называются. Например, низкого и среднего уровня сложности, повышенной трудности и олимпиадные. В сборниках они обозначаются разным способом. Признаки классификации и критерии отнесения задач к тому или иному уровню при этом не указываются.
Учитель, готовясь к урокам, как правило, подбирает задачи из многих сборников. При этом для него важен не только обозначенный уровень сложности (трудности) задачи, но и разъяснение, почему эта задача отнесена к тому или иному уровню, т.е. учителю важно знать признаки классификации физических задач по уровням трудности (сложности). Это важно не только для грамотного подбора задач, но и помогает составлять их (или частично изменять).
Понятия «сложность задачи» и «трудность задачи» часто в методике преподавания физики применяются как понятия-синонимы, поскольку ими характеризуется и субъективная сторона задачи – сможет ли ее решить школьник или не сможет.
Трудность задачи в большей степени характеризует процесс ее решения, чем содержание, сложность же – наоборот.
Наряду с субъективными признаками рассматриваемых понятий имеются и объективные. Их можно выделить исходя из анализа структуры физической задачи, который может выглядеть так:
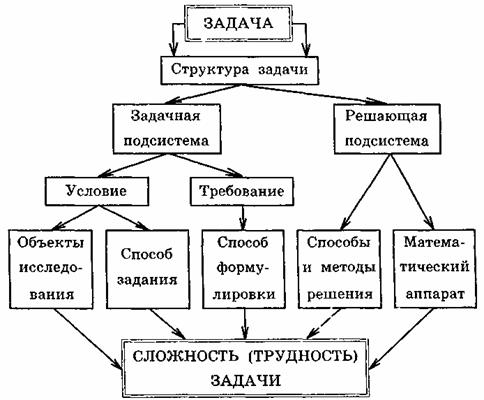
Линиями, проведенными к блоку "сложность задачи", отмечены существенные признаки этого понятия. Рассмотрим роль и значение каждого из них.
В качестве объектов исследования в задаче могут быть отдельные тела или системы тел, состояние которых изменяется в результате взаимодействия с другими телами. Во многих случаях объект исследования - явление (процесс) или несколько процессов. Явления и процессы находятся в определенной взаимосвязи. С учетом того, что характерной особенностью познания является модельность представлений, отдельные связи между объектами исследования можно не учитывать.
По способу задания условия различают задачи-рисунки, текстовые, графические и экспериментальные задачи. Наиболее трудно воспринимается учащимися условие, заданное графическим и экспериментальным способами.
Требование задачи может быть сформулировано в явном или неявном виде. В явном виде требование формулируется в том случае, когда необходимо найти значение одной или нескольких физических величин, являющихся характеристиками объектов исследования.
При решении задач в качестве средства применяется тот или иной математический аппарат, который можно классифицировать как простой, не очень сложный и сложный.
В теории задач выделяют такие способы их решения, как логический, арифметический, алгебраический, геометрический и графический. Способ решения задачи определяется применяемыми средствами решения. Основными методами решения задач являются аналитический и синтетический.
При применении аналитического метода решения задач вывод расчетной формулы начинают с установления связи между требованием и другими величинами (данными в условии задачи, постоянными, коэффициентами и с величинами, значение которых неизвестно, но может быть найдено через известные в задаче величины).
Применение синтетического метода решения задач предполагает поиск расчетной формулы в обратном порядке [1].
Сложность выбранного способа и метода решения задачи - субъективный фактор, определяющий сложность (трудность) задачи. Его можно значительно ослабить путем ознакомления учащихся со структурой задач, методами и способами их решения [1].
Исходя из сказанного выше можно охарактеризовать уровни сложности (трудности) задач следующим образом.
|
Уровень сложности (трудности) задачи |
Объекты исследования |
Требование задачи |
Математический аппарат |
Способ задания условия |
|
1 |
Одно явление один процесс) L-2 объекта |
Найти значение 1-2 физических величин. Задано в явном виде |
Простой |
Текстовый. Задача-рисунок |
|
2.1 |
Одно явление (один процесс) 1-2 объекта |
Задано в неявном виде |
Не очень сложный |
Любой |
|
2.2 |
Два-три явления (процесса) 2-3 объекта |
Найти значение нескольких физических величин. Задано в явном виде |
Не очень сложный |
Любой |
|
3.1 |
Два-три явления (процесса) 2-3 объекта исследования |
Задано в неявном виде |
Не очень сложный |
Любой |
|
3.2 |
Более трех явлений (процессов, трех объектов) |
Найти значение нескольких физических величин. Задано в явном виде |
Не очень сложный |
Любой |
|
4 |
Более трех явлений (процессов, трех объектов) |
Задано в неявном виде |
Сложный |
Любой |
Приведем примеры физических задач, отнесенных к выделенным уровням сложности (трудности):
1. С высоты 20 м свободно падает маленький шар. Найдите время падения шара и его скорость в момент касания поверхности земли.
2.1. С высоты 20 м свободно падает маленький шар. Каково его перемещение за последнюю секунду падения?
2.2. С высоты 20 м свободно падает маленький шар на движущуюся вверх со скоростью 5 м/с горизонтальную подставку. Найдите скорость шарика в момент касания подставки.
3.1. С высоты 20 м свободно падает маленький шар на движущуюся вверх со скоростью 5 м/с подставку. Найдите перемещение шарика в последнюю секунду падения и время движения на последнем метре пути.
3.2. С высоты 20 м вертикально вниз бросили маленький шар со скоростью 5 м/с. С высоты 2 м вертикально вверх одновременно бросили второй такой же шарик со скоростью 10 м/с. Точки бросания шаров находятся на одной вертикали.
Постройте график зависимости расстояния между шариками от времени.
4. С высоты 20 м вертикально вниз бросили резиновый шар со скоростью 5 м/с на край наклонной плоскости с углом наклона 30° и длиной 5 м. Сколько ударов шара произойдет о наклонную плоскость? Как изменится число ударов, если наклонная плоскость будет двигаться горизонтально со скоростью 5 м/с?
Во всех приведенных задачах описана одна и та же за-дачная ситуация с незначительными изменениями. Предложенную систему задач достаточно легко трансформировать в многоуровневую физическую задачу. Вот какой вид она будет иметь.
С высоты 20 м на подставку свободно падает маленький шар.
1. Найдите время падения шара и его скорость в момент касания поверхности подставки.
2. Найдите перемещение шара за последнюю секунду падения.
3. Найдите перемещение шара за последнюю секунду, если подставка движется вертикально вверх со скоростью 5 м/с.
4. Найдите время движения шара на последнем метре пути.
5. Навстречу падающему шару с высоты 2 м одновременно с началом движения первого бросают другой такой же шар.
Постройте график зависимости расстояния между шарами от времени, если первоначально шары находятся в точках на одной вертикальной линии.
6. Как изменится график зависимости расстояния между шарами от времени, если первоначально шары находятся в точках, отстоящих по горизонтали на расстоянии 2 м?
7. Резиновый шар падает на край наклонной плоскости с углом наклона 30° и длиной 5 м. Сколько ударов шара произойдет о наклонную плоскость?
8. Как изменится число ударов резинового шара о наклонную плоскость, если она будет двигаться со скоростью 5 м/с?
Преимущество многоуровневых задач было описано автором в одной из публикаций [2].
1. Кротау В.М. Дыферэнцыяцыя навучання вучняу рашэнню задач па фiзiцы // Народная асвета. – 1996. – №5. – С. 99-110.
2. Кротов В.М. Многоуровневые задачи по физике // Фiзiца: праблемы выкладання. – 1997. – №7. – С. 88-90.
| Выложил | alsak |
| Опубликовано | 12.08.13 |
| Просмотров | 8635 |
| Рубрика | Методика | Решение задач |
| Тема | Без тем |