Купрацевич О.А. Особенности работы с графиками при решении задач по теме «Основы термодинамики»
Купрацевич О. А. Особенности работы с графиками при решении задач по теме «Основы термодинамики» // Фізіка: праблемы выкладання. — 2009. — № 5. — С. 28—36.
Анализируя содержание тестовых заданий, предлагавшихся во время вступительных кампаний прошлых лет, можно заметить, что в условиях многих из них содержится информация, представленная в виде схем, рисунков, графиков. Сталкиваясь именно с такими задачами, абитуриенты, как правило, либо допускают ошибки, либо вовсе не знают, как приступить к решению, поскольку испытывают затруднения при анализе предложенной иллюстративной информации. Задачи такого плана относятся ко всем разделам курса физики, поэтому общим залогом верного решения является анализ предложенной информации и полное использование данных, представленных на рисунке. Из всех задач, предлагавшихся на централизованном тестировании, в данной статье рассматриваются задачи с использованием диаграммы состояния идеального газа. Причём из года в год количество абитуриентов, верно решивших подобные задачи, невелико. Конечно, большинство задач такого плана относятся к 4—5-му уровню сложности, но при этом всё же есть некие общие подходы, позволяющие подготовить учащихся к их решению.
Предлагаю вниманию читателей задачу, на примере которой можно увидеть, какими опорными знаниями должны обладать учащиеся для успешного решения задач данного типа.
Задача 1. С одним киломолем идеального одноатомного газа осуществляется цикл, изображённый на рисунке в координатах (V, Т) (рис. 1). Газ последовательно про
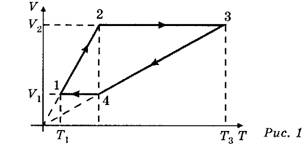
ходит состояния 1—2—3—4—1. Температура газа в состоянии 1 T1= 200К и в состоянии 3 — Т3= 800 К. Найдите работу, совершённую газом за один цикл.
Решать эту задачу следует после усвоения следующих основных понятий и знаний.
I. Учащиеся должны чётко представлять, как выглядят графики соответствующих изопроцессов в различных координатах. Для этого целесообразно в ходе объяснения ввести понятие так называемых родных координат, т.е. таких координат, в которых присутствовали бы только изменяющиеся параметры: для изотермического процесса — (р, V), для изохорного — (р, Т), для изобарного — (V, Т) (рис. 2).
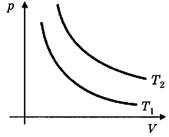
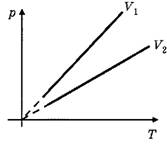
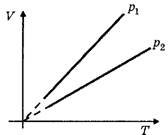Рис. 2
Как показывает практика, для того, чтобы сформировать у учащихся навыки быстрого определения, какой изотерме, изобаре, изохоре в "родных координатах" соответствует большее значение Т, р и V, необходимо изначально дать им возможность самостоятельно выйти на соответствующую закономерность. Как правило, учащиеся быстро замечают, что изотерма, лежащая выше, соответствует большей температуре (Т2> T1), изохора, лежащая ближе к оси температур, соответствует большему объёму (V2>V1), а изобара, лежащая ближе к оси температур, соответствует большему давлению (р2> P1)-При этом, конечно, следует заметить, что все диаграммы состояния идеального газа соответствуют одному и тому же количеству вещества.
После усвоения этого блока информации учащиеся должны без затруднений решать задачи следующего типа.
Задача 2. Как изменяется температура газа при переходе из состояния 1 в состояние 2 (рис. 3)?
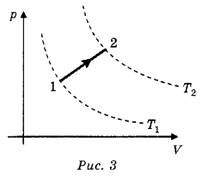
Решение. Так как точка 2 соответствует более высокой изотерме, то температура газа увеличивается. (Изотермы, изображённые на чертеже, появляются в ходе решения.)
Задача 3. Как изменяется объём газа при переходе из состояния 1 в состояние 2 (рис. 4)?
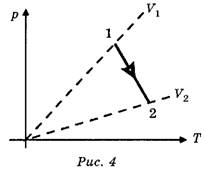
Решение. Точка 2 принадлежит изохоре, лежащей ближе к оси температур, следовательно, объём газа увеличивается.
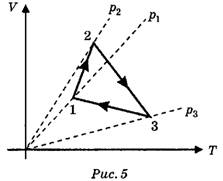
Задача 4. Как изменяется давление газа в ходе представленного циклического процесса (рис. 5)? (Решение этой задачи очевидно.)
II. Необходимо уметь представлять циклический процесс в любых координатах. Для успешного выполнения подобных заданий следует показать учащимся алгоритм построения графиков.
Рассмотрим пример. Дан циклический процесс в координатах (р, V) (рис. 6), нужно построить этот же процесс в других координатах.
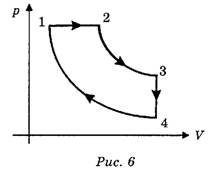
Решение. Прежде всего необходимо начертить недостающие системы координат (рис. 7). В нашем случае это (р, Т) и (V, Т). Системы координат следует размещать таким образом, чтобы соответствующие оси были параллельны. Прежде чем выполнять построение, необходимо проанализировать каждый участок циклического процесса и описать, как меняются параметры, указав соответствующие параметры на чертеже.
(1—2) изобарное нагревание;
(2—3) изотермическое расширение;
(3—4) изохорное охлаждение;
(4—1) изотермическое сжатие.
(1→2) р=const, V↑, Т↑;
(2→3) Т=const, V↑ , Т↓ ;
(3→4) V=const, T↓, p↓;
(4→1) T=const, p↑, V↓.
(Знаки ↑и ↓ означают соответственно увеличение и уменьшение того или иного параметра.)
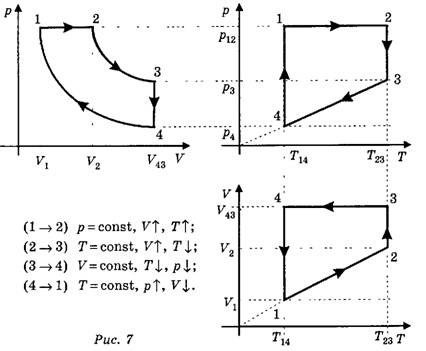
После этого надо провести соответствующие изотермы, изобары и изохоры штрихпунктирными линиями. Каждая изохора, изобара и изотерма соответствует определённому переходу и обозначается соответствующими индексами. Точки пересечения соответствуют номеру состояния. Например, в координатах (р, Т) состояние 1 соответствует пересечению изобары р12 и изотермы Т14 состояние 2 соответствует пересечению изобары p12 и изотермы T23, состояние 3 соответствует пересечению изобары p3и изотермы T23, состояние 4 соответствует пересечению изобары р4 и изотермы T14. После того как точки определены, соединяем их соответствующими линиями, при этом каждый участок цикла анализируем в соответствии с полученным ранее описанием.
{mospagebreak}
III. Для успешного решения задач с использованием диаграмм состояния идеального газа следует заострить внимание учащихся на том, что работа в термодинамике может быть рассчитана как площадь фигуры, ограниченной диаграммой процесса только в координатах (р, V). Если процесс представлен в других координатах, необходимо представить процесс в координатах (р, V ).
IV. Кроме того, необходимо показать учащимся, что каждой точке на диаграмме состояния соответствует уравнение состояния (рис. 8).
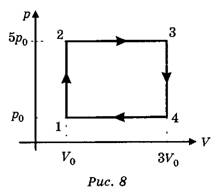
Например,для состояния
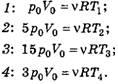
Теперь можем приступить к решению задачи 1. Проанализировав замкнутый циклический процесс, понимаем, что необходимо изобразить данный процесс в осях (р, V) (рис. 9). (Воспользуемся рекомендациями пункта II.)
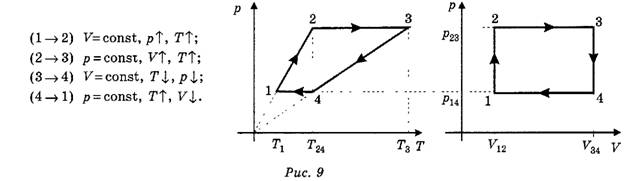
Можно заметить, что
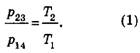
Учитывая, что T2= T4 получаем:
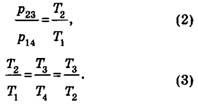
Следовательно,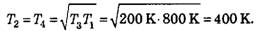
Учитывая выражение (2), получаем P23/P14=2
Так как V34/T4=V12T1 получаем V34/T4= 2.
Теперь можно перестроить диаграмму состояния с учётом полученых соотношений. Будем считать, что
p14=p0, p23=2р0, V12=V0 , V34=2V0.
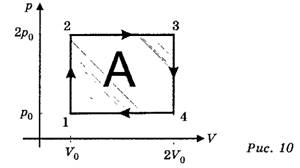
Теперь запишем уравнение состояния для любой точки цикла.
Для состояния 1: p0V0=vRT1, следовательно, A = vRT1.
Произведём расчёт:
А=103*8,31(Дж/моль*К) *200К = 16,62 Дж.
Предлагаю читателям для самостоятельного решения ещё две задачи.
Задача 5. В циклическом процессе участвует v = l,5 моль идеального газа. Направление процесса указано стрелками (рис. 11).
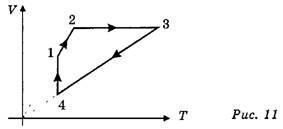
Найдите работу, совершённую газом за цикл, если на участке 1—2 он отдаёт холодильнику количество теплоты Q=2740 Дж. Температуры в состоянии 3 и 4 соответственно T3 = 600 К и T4=300 К.
Ответ: A=-Q+vR(T3-T4)=1000 Дж.
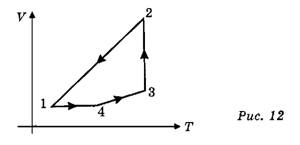
Задача 6. С четырьмя молями идеального газа совершают циклический процесс в направлении, показанном на рисунке (рис. 12). На участке 3—4 газу передаётся количество теплоты Q- 2200 Дж. Температуры в состояниях 1 и 2 соответственно Т1 = 373 К, Т2 = 423 К. Найдите работу, совершаемую газом за цикл.
Список использованной литературы
1. Турчина, Н. В. 3800 задач для школьников и поступающих в вузы / авт.-сост. JI. И. Рудакова [и др.]. — М. : Дрофа, 2000. — 672 с.
2. Физика: готовимся к централизованному тестированию: Некоторые особенности ЦТ 2008 г. Методика расчёта тестового балла. Решения и комментарии к контрольному тесту. Тренировочные тесты / Респ. ин-т контроля знаний М-ва образования Респ. Беларусь. — Минск: Юнипресс, 2009. — 128 с.
| Выложил | alsak |
| Опубликовано | 14.03.12 |
| Просмотров | 31138 |
| Рубрика | Решение задач |
| Тема | Термодинамика |