Сакович А.Л. Сложность физических задач и их уровни
С переходом республики Беларусь на поуровневый подход к оценке учебных достижений учащихся возникает необходимость создания соответствующего дидактического пособия. При этом требуется решить несколько проблем, две из которых рассмотрим в данной статье: 1) способ определения сложности задач; 2) критерий деления задач по уровням. Доказательством актуальности данных проблем может служить новый сборник заданий по физике для проведения выпускных экзаменов [7], в котором каждый автор сборника по-своему определяет сложность задач, в итоге задача 4 уровня может оказаться проще задачи 3 уровня.
В обиходной речи, а нередко и в научной литературе, при описании задач «сложность» заменяют термином «трудность» и, наоборот [1, с. 112]. В то же время ряд авторов (Балл Г.А. [1, с. 112], Гузеев В.В. [3, с. 51, 54] и др.) считают, что эти понятия надо разделять. Сложность – это объективная характеристика задачи, «которая определяется структурой процесса поиска решения» [3, с. 51]. А «трудность задачи является субъективной характеристикой, т.е. зависит от того, кто решает эту задачу. … Она может зависеть от объема и подвижности памяти ученика, его предыдущего опыта, состояния здоровья и многих других факторов. Одна и та же задача может быть трудной для одних учеников и легкой для других, или трудной при наличии одних ресурсов и легкой при возможности использовать другие ресурсы» [3, с. 54].
В научной литературе нет единого подхода к выбору компонентов сложности задач. Так Соколова Л.Г. выявила шесть таких компонентов: «1. Не все элементы, характеризующие процесс или явление (как-то: физические величины, условия и т. п.), заданы явно. 2. В физической ситуации проявляют себя несколько закономерностей – связей физических величин. 3. Задача не типовая, а комплексная, относящаяся к нескольким типам учебных задач. 4. Задача не элементарная, а комбинированная (возможно расчленение задачи на элементарные, связанные с одним физическим телом или с одним его состоянием и т. п.). 5. Не все величины, указанные в условии задачи, заданы в одной системе единиц измерения физических величин. 6. Нахождение искомой величины связано с проделыванием большого количества математических операций (задача не прямая, а обратная; искомое находится путем решения системы многих уравнений и т.п.)» [8, с. 62]. А Лернер И.Я. считает, что «сложность задач … зависит от трех факторов: 1) от количества данных в условии, подлежащих учету и взаимному соотнесению для успешного решения; чем больше таких данных, тем сложнее задача; 2) от расстояния между вопросом задачи и ответом на нее, т.е. от числа промежуточных операций (суждений), логических звеньев, которые необходимо пройти, чтобы найти решение; 3) от состава решения, т.е. от числа рядоположных выводов, которые можно и нужно сделать в результате решения задачи» [6, с. 48-49].
Не выработана до сих пор и единая методика расчета сложности задач, хотя работы в этом направлении ведутся. Так представляет интерес алгоритмический подход Г.А. Балла. В соответствии с ним сложность задачи оценивают по количеству операций в алгоритмическом способе ее решения [1, с. 121]. Но алгоритмический способ имеет ряд ограничений: 1) для очень многих задач, особенно творческих, не удается описать алгоритмических способов их решения; 2) отдельные виды операций могут существенно различаться между собой по трудности; 3) задача может иметь несколько решений и т.д. [1, с. 124-125]. При определенных условиях эти ограничения можно снять, но это значительно усложнит способ его применения.
Проще в обращении таблица определения уровня сложности задач Кротова В.М., полученная исходя из анализа структуры физической задачи. Уровень задач у автора определяется: 1) объектами исследования (число явлений, процессов и объектов); 2) требованием задачи (задано требование в явном или неявном виде, и число физических величин, значения которых надо найти); 3) математическим аппаратом (простой, не очень сложный, сложный); 4) способом задания условия (задачи-рисунки, текстовые, графические или экспериментальные задачи) [5, с. 72].
Но сложность задачи определяется структурой процесса поиска ее решения, поэтому более логично составлять таблицу уровней задач, анализируя все же последнюю структуру.
Для анализа воспользуемся структурой учебной деятельности по решению задач, предложенной Усовой А.В. и Тулькибаевой Н,Н. [10, с. 27, 61-63].
I. Ознакомление с условием задачи.
Это действие состоит из четырех операций:
I.1. Чтение задачи.
|
критерии деления |
Уровни |
|
|
Способ задания |
задачи-рисунки, текстовые |
1-5 |
|
графические |
3-5 |
|
|
экспериментальные |
4-5 |
|
I.2. Восприятие содержания задачи (выделение описанного в задаче явления, процесса или объекта).
|
Критерии деления |
Уровни |
||
|
Вид данных |
в норме |
1-5 |
|
|
недостающие |
4-5 |
||
|
лишние |
3-5 |
||
|
Число |
явлений, процессов |
1 |
1-5 |
|
2, 3 |
3-5 |
||
|
больше 3 |
4-5 |
||
|
объектов |
1 |
1-5 |
|
|
2, 3 |
3-5[1] |
||
|
больше 3 |
4-5 |
||
|
состояний объекта |
1, 2 |
1-5 |
|
|
3 |
3-5 |
||
|
больше 3 |
4-5 |
||
I.3. Краткая запись условия и требования задачи; выполнение рисунков, схем, чертежей, поясняющих задачу[1].
[1] Не совсем понятна позиция авторов сборников задач, когда они даже для задач 3-5 уровня указывают в условии обозначение физических величин.
В задачах 1 уровня эти действия не выполняются. Здесь также не требуется найти значения величин. Для задач 2 уровня не надо выполнять рисунки, схемы, чертежи, поясняющие задачу. При необходимости, все это должно быть дано в готовом виде.
|
Критерии деления |
Уровни |
|
|
Краткая запись условия |
2-5 |
|
|
Поясняющие рисунки, схемы, графики |
3-5 |
|
|
Вид требования |
явный |
1-5 |
|
не явный |
3-5 |
|
|
Число физических величин, которых требуется найти |
1 |
2-5 |
|
2, 3 |
3-5 |
|
|
больше 3 |
4-5 |
|
I.4. Воспроизведение содержания задачи по ее краткой записи.
Данная операция редко используется на практике.
II. Составление плана решения задачи.
Данное действие редко используется на практике.
III. Осуществление решения задачи.
III.1. Выделение способа решения задачи.
В методике физики по способу решения выделяют: «качественные (задачи-вопросы), вычислительные, графические и экспериментальные задачи» [9, с. 321].
По содержанию условий и требований выделяют три вида качественных (логических) задач: 1) на узнавание в конкретном явлении физического явления; 2) объяснение явления и свойств тел; 3) предсказание следствия происходящего явления [10, с. 119]. Здесь же можно добавить и задания, которые требуют, чтобы учащийся узнавал «физические модели, объекты, явления, формулы, приборы при предъявлении их в готовом виде»; различал «определения понятий, величин, законов, моделей, теорий и др., когда они предъявляются ему в готовом виде, однако самостоятельно воспроизвести не может» [4, с. 269].
По функции графика выделяют несколько видов графических задач: 1) задачи, в которых график задается в условии и его надо проанализировать; 2) задачи, в которых в условии или в процессе решения требуется графически выразить зависимость между физическими величинами [9, с. 327; 10, с. 112].
По роли эксперимента выделяем следующие виды экспериментальных задач: 1) задачи, в которых без эксперимента нельзя получить ответ; 2) задачи, в которых эксперимент используется для создания определенной ситуации; 3) задачи, в которых эксперимент используется для иллюстрации описанного явления; 4) задачи, в которых эксперимент используется для проверки полученного результата [10, с. 123].
При решении вычислительных задач используют «арифметический, алгебраический, графический, геометрический способы» [9, с. 325]. В пособиях для учителей физики можно встретить описание и других способов (нестандартных методов) решения задач [3], которые применяются в основном для решения задач «повышенной трудности».
|
Критерии деления |
Уровни |
|||
|
Виды задач |
качественные |
на узнавание и различение моделей, объектов, явлений и т.д. при предъявлении их в готовом виде |
1-5 |
|
|
на узнавание в конкретном явлении физического явления; на объяснение явления и свойств тел |
3-5 |
|||
|
на предсказание следствия происходящего явления |
4-5 |
|||
|
графические |
график задается в условии и его надо проанализировать |
3-5 |
||
|
в условии или в процессе решения требуется графически выразить зависимость между физическими величинами |
линейная зависимость |
3-5 |
||
|
не линейная зависимость |
4-5 |
|||
|
экспериментальные |
4-5 |
|||
|
Способы решения вычислительных задач |
арифметический |
2-3 |
||
|
алгебраический, геометрический |
2-5 |
|||
|
графический |
3-5 |
|||
|
нестандартный |
3[1]-5 |
|||
[1] Задачи 3 и 4 уровня имеют стандартное (алгоритмическое) решение, хотя нестандартные способы могут применяться изредка и здесь.
III.2. Выделение и запись основного уравнения (выделенных суждений), определение достаточности его для получения соотношения между требованием и условием.
В задачах 1 уровня уравнения не записываются – они даются в готовом виде.
|
Критерии деления |
Уровни |
||
|
Число |
уравнений |
1 (1+1[1]) |
2-5 |
|
2, 3 |
3-5 |
||
|
больше 3 |
4-5 |
||
|
тем (разделов) |
1 |
2-5 |
|
|
2[2] |
3-5 |
||
|
больше 2 |
4-5 |
||
|
Вид функций [2, с. 26, 44-56] |
линейная, обратная пропорциональность, квадратичная, степенная, тригонометрические |
2-5 |
|
|
обратные тригонометрические |
3-5 |
||
|
показательные[3], логарифмические |
4-5 |
||
|
Вид геометрических соотношений |
элементарные (формулы площади треугольника, прямоугольника, трапеции, круга, длины окружности, проекции вектора, теорема Пифагора и т.п.) |
2-5 |
|
|
простые (формулы площади поверхности и объема объемных фигур, проекции суммы или разности векторов, расположенных вдоль одной прямой и т.п.) |
3-5 |
||
|
средней сложности (теоремы синусов, косинусов, формулы площади секторов, проекции суммы или разности векторов, расположенных под углом друг к другу и т.п.) |
4-5 |
||
|
сложные (координатные формулы скалярного и векторного произведения; уравнения линий второй степени и т.п.) |
5 |
||
|
Неравенства |
4-5 |
||
|
Высшая математика |
4-5 |
||
[1] Во 2 уровне дополнительно к физической формуле может быть одно простейшее геометрическое уравнение.
[3] Исключение, закон радиоактивного распада (показательная функция) может применяться в задачах 2 уровня.
III.3. Осуществление преобразования исходного уравнения (высказываний) или системы уравнений с включением дополнительных с целью получения соотношения между требованием и условием задачи.
В задачах 1 уровня уравнения не преобразовываются.
|
Критерии деления |
Уровни |
||
|
Число преобразований исходного уравнения |
1, 2 |
2-5 |
|
|
3, 4 |
3-5 |
||
|
больше 4 |
4-5 |
||
|
Вид преобразуемых функций |
линейная, обратная пропорциональность, степенная |
2-5 |
|
|
тригонометрическая |
3-5 |
||
|
квадратичная |
4-5 |
||
|
показательная, логарифмическая |
5 |
||
Зависимость уровней от вида преобразуемых геометрических соотношений учитывать не будем, т.к. уровень будем примерно соответствовать уровню применяемых геометрических соотношений (см. пункт III.2).
III.4. Проверка правильности полученного соотношения между требованием и условием задачи (выполнение действий с наименованиями).
Данная операция выполняется для задач 3-5 уровня.
IV. Проверка полученного решения задачи.Данное действие выполняется для задач 4-5 уровня. Отдельно операции рассматривать не будем.
Все приведенные выше таблицы сведем в одну (см. приложение).
Проверим совместимость предложенного метода с примерными нормами оценки результатов учебной деятельности учащихся по физике [4, с. 266-277].
1 уровень: «учащийся узнает физические модели, объекты, явления, формулы, приборы при предъявлении их в готовом виде; … различает определения понятий, величин, законов, моделей, теорий и др., когда они предъявляются ему в готовом виде, однако самостоятельно воспроизвести не может» [4, с. 269], т.е. задачи на этом уровне не решаются; задания только в виде тестов.
2 уровень: «учащийся … умеет решать одношаговые задачи по образцу (записывает краткое условие с помощью символов, переводит значения величин в СИ, находит нужную формулу, подставляет значения физических величин, вычисляет, оценивает ответ и записывает его)» [4, с. 269]. Различие в том, что нами было увеличено число шагов до двух за счет преобразования формулы, а действие «оценивает ответ» перенесено в 3 уровень.
3 уровень: «учащийся … без затруднений переводит словесную информацию в графическую или символьную. … Решает расчетные двухшаговые задачи, умеет читать и строить графики, делать рисунки, решать несложные качественные задачи, опираясь на необходимые теоретические знания» [4, с. 270]. В этом уровне впервые упоминаются графические и качественные задачи, поясняющие рисунки, что соответствует нашим предложениям. Различие в том, что нами число шагов увеличено до четырех.
4 уровень: «учащийся применяет теоретические знания для решения экспериментальных, расчетных, качественных и графических многошаговых задач по алгоритму, владеет способами самоконтроля. Имеет навыки обращения с физическими приборами ... применяет знания теоретического материала для решения комбинированных многошаговых задач (необходимы знания из разных разделов физики) всех типов по известному алгоритму, самостоятельно исправляет допущенные ошибки» [4, с. 270]. В этом уровне впервые упоминаются экспериментальные и комбинированные задачи, способы самоконтроля (проверки); число шагов не ограничено, что соответствует нашим предложениям. Различие в том, что кроме алгоритмического решения задач нами допускаются нестандартные методы решения.
5 уровень[1]: «учащийся применяет теоретический материал для решения задач в субъективно новой ситуации, для чего «переносит» знания из других разделов физики или других учебных предметов. … решает нестандартные физические задачи, в том числе задачи с неопределенным условием; создает новые алгоритмы решения, составляет задачи, выполняет исследовательские лабораторные работы (без инструкции)» [4, с. 270-271]. В этом уровне различий нет.
[1] Автор придерживается мнения Гузеева В.В. о том, что «учебная деятельность всегда является воспроизводящей… Творческая деятельность может присутствовать в любом типе учебной деятельности», но это не новый тип учебной деятельности (см. Гузеев В.В. Планирование результатов образования и образовательная технология. М.: Народное образование, 2001. – С. 48). Высший школьный уровень – четвертый, и он должен оцениваться максимальной отметкой. Творческая работа нужна для одаренных детей. Отметка за нее может быть, но она должна играть роль поощрения (вместо похвальных грамот, дипломов) и не должна никаким образом влиять на аттестат.
Исходя из выше изложенного следует, что наши рекомендации не ослабили уровни (за исключением 2 уровня, убрав действие оценивания ответа), а даже усложнили их.
{mospagebreak} Для примера, используя предложенный нами метод, определим уровни некоторых задач из темы «Конденсаторы. Энергия электрического поля» из Сборника заданий по физике для проведения выпускных экзаменов за курс средней школы, тестирования, вступительных экзаменов в высшие учебные заведения [7]. Рассматривать будем только операции не соответствующие данному уровню.
Задача 60* (1 уровень). На каком из графиков (рис. 5) изображена зависимость емкости плоского конденсатора С от расстояния между его обкладками d?
Условие задачи задано графиком, следовательно, это задача не ниже 3 уровня. Это качественная задача (тест), но не на опознание и различение (знание о графике зависимость емкости плоского конденсатора от параметров конденсатора не входит в перечень основных знаний и умений учащихся). Используемая функция – обратная пропорциональность, но уравнение дано не в готовом виде, а его надо еще записать – задача не ниже 2 уровня.
Делаем вывод – задача 3 уровня.
Задача 96 (2 уровень). Определите емкость и заряд плоского слюдяного конденсатора с площадью обкладок S = 36 см2 каждая, которые находятся на расстоянии d = 1,4 мм, если напряжение между обкладками конденсатора U = 300 В.
Для решения задачи необходимы две физические формулы: ![]() .
.
Делаем вывод – задача 3 уровня.
Задача 288 (3 уровень). Определите напряженность электростатического поля Е между обкладками плоского воздушного конденсатора емкостью С, если их заряды q1 = –2q и q2 = +3q соответственно. Расстояние между обкладками равно d.
Для решения задачи необходимы четыре физические формулы: 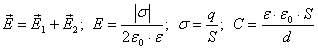 – не ниже 4 уровня.
– не ниже 4 уровня.
Число преобразований: 1) нахождение проекций уравнения; 2) вывод формулы 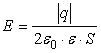 ; 3)-4) вывод формулы
; 3)-4) вывод формулы ![]() ; 5) - 6) вывод итоговой формулы
; 5) - 6) вывод итоговой формулы ![]() , – не ниже 4 уровня.
, – не ниже 4 уровня.
Делаем вывод – задача 4 уровня.
Выполняя аналогичные действия для остальных задач этой темы[1], распределим их по уровням следующим образом:
[1] Аналогичная таблица составлена по всей теме «Электростатика».
|
Номер задачи |
Уровень сборника |
Новый уровень |
Номер задачи |
Уровень сборника |
Новый уровень |
Номер задачи |
Уровень сборника |
Новый уровень |
|
9 |
1 |
1 |
198 |
2 |
3 |
402 |
3 |
3 |
|
10 |
1 |
1 |
199 |
2 |
3 |
403 |
3 |
3 |
|
11 |
1 |
1 |
200 |
2 |
3 |
485 |
4 |
4 |
|
12 |
1 |
1 |
288 |
3 |
4 |
494 |
4 |
4 |
|
13 |
1 |
1 |
289 |
3 |
4 |
495 |
4 |
5 |
|
60 |
1 |
3 |
290 |
3 |
3 |
496 |
4 |
5 |
|
61 |
1 |
3 |
291 |
3 |
3 |
497 |
4 |
4 |
|
92 |
2 |
2 |
292 |
3 |
4 |
498 |
4 |
4 |
|
93 |
2 |
2 |
293 |
3 |
4 |
499 |
4 |
4 |
|
94 |
2 |
2 |
294 |
3 |
3 |
500 |
4 |
4 |
|
95 |
2 |
2 |
295 |
3 |
3 |
501 |
4 |
3 |
|
96 |
2 |
3 |
296 |
3 |
3 |
502 |
4 |
3 |
|
97 |
2 |
3 |
297 |
3 |
3 |
|||
|
197 |
2 |
3 |
298 |
3 |
? |
1. Балл Г.А. Теория учебных задач: Психолого-педагогический аспект. – М.: Педагогика, 1990.– 184 с.
2. Воднев В.Т. и др. Основные математические формулы: Справочник / Под ред. Ю.С.Богданова. – Мн.: Выш. шк., 1995. – 380 с.
3. Гузеев В.В. Соотнесение сложности и трудности учебных задач с уровнями планируемых результатов обучения // Школьные технологии. – 2003. – №3. – С. 50-56.
4. Десятибалльная система оценки результатов учебной деятельности учащихся: Инструктивно-метод. материалы / Под ред. О.Е. Лисейчикова. – Мн.: НИО, 2002. – 400 с.
5. Кротов В.М. К вопросу о сложности (трудности) физических задач // Фiзiка: праблемывыкладання. – 1999. – №3. – С. 69-74.
6. Лернер И.Я. Проблемное обучение. – М., 1974.
7. Сборник заданий по физике для проведения выпускных экзаменов за курс средней школы, тестирования, вступительных экзаменов в высшие учебные заведения / Авт.-сост. В.В. Жилко, Л.А. Исаченкова, А.А. Луцевич и др. – Мн.: Адукацыяiвыхаванне, 2003. – 544 с.
8. Соколова Л.Г. О формировании у студентов физического факультета умений обучать учащихся решению задач // Современные психолого-педагогические проблемы высшей школы. Вып. I. Л., 1973. – С. 60-63.
9. Теория и методика обучения физике в школе: Общие вопросы / Под ред. С.Е. Каменецкого, Н.С. Пурышевой. – М.: Издательский центр «Академия», 2000. – 368 с.
10. Усова А.В., Тулькибаева Н.Н. Практикум по решению физических задач. – М.: Просвещение, 1992. – 208 с.
Таблица
Уровни задач
|
Уровень |
I. Условие задачи |
||||||||
|
I.1. Способ задания |
I.2. Содержание |
I.3. Запись условия |
|||||||
|
Вид данных |
Число |
Краткая Запись |
Поясняющие рисунки, схемы, графики |
Требования |
|||||
|
Явлений, процессов |
Объектов |
Состояний объекта |
Вид |
Число величин |
|||||
|
I |
Задачи-рисунки, текстовые |
В норме |
1 |
1 |
1, 2 |
Нет |
Нет |
Явный |
Нет |
|
II |
То же |
В норме |
1 |
1 |
1, 2 |
Может быть |
Нет |
Явный |
1 |
|
III |
Задачи-рисунки, текстовые, графические |
В норме и лишние |
1-3 |
1-3 |
1-3 |
Может быть |
Может быть |
Любой |
1-3 |
|
IV |
Задачи-рисунки, текстовые, графические, экспериментальные задачи |
Любые |
Любое |
Любое |
Любое |
Может быть |
Может быть |
Любой |
Любое |
|
V |
То же |
Любые |
Любое |
Любое |
Любое |
Может быть |
Может быть |
Любой |
Любое |
Продолжение
|
Уровень |
III. Решение задачи |
|||||||
|
III.1. Способы решения |
||||||||
|
Качественные |
Графические |
Экспериментальные |
Вычислительные |
|||||
|
Арифметический |
Алгебраический |
Геометрический |
Графический |
Нестандартные методы |
||||
|
I |
На узнавание и различение моделей, объектов, явлений и т.д. при предъявлении их в готовом виде |
Нет |
Нет |
Нет |
Нет |
Нет |
Нет |
Нет |
|
II |
То же |
Нет |
Нет |
Есть |
Есть |
Есть |
Нет |
Нет |
|
III |
На узнавание и различение моделей, объектов, явлений и т.д. при предъявлении их в готовом виде; на объяснение явлений |
Анализ графика; построение графика линейной функции |
Нет |
Есть |
Есть |
Есть |
Есть |
Редко |
|
IV |
Любые |
Любые |
Любые |
Нет |
Есть |
Есть |
Есть |
Редко |
|
V |
Любые |
Любые |
Любые |
Нет |
Есть |
Есть |
Есть |
Есть |
Продолжение
|
Уровень |
III. Решение задачи |
IV. Проверка |
|||||||
|
III.2. Запись уравнений |
III.3. Преобразования уравнений |
||||||||
|
Вид функций |
Неравенства |
Высшая математика |
Геометрическиесоотношения |
Число |
Вид функций |
Число преоб-разований |
|||
|
тем |
уравнений |
||||||||
|
I |
Нет |
Нет |
Нет |
Нет |
Нет |
Нет |
Нет |
Нет |
Нет |
|
II |
Линейная, обратная пропорциональность, квадратичная, степенная, тригонометрические |
Нет |
Нет |
Элементарные |
1 |
1+1 |
Линейная, обратная пропорциональность, степенная |
1-2 |
Нет |
|
III |
Линейная, обратная пропорциональность, квадратичная, степенная, тригонометрические, обратные тригонометрические |
Нет |
Нет |
Элементарные, простые |
2 |
1-3 |
Линейная, обратная пропорциональность, степенная, тригонометрическая |
1-4 |
Действия с наименованиями |
|
IV |
Любые |
Есть |
Нет |
Элементарные, простые, средней сложности |
Любое |
Любое |
Линейная, обратная пропорциональности, степенная, тригонометрическая, квадратичная |
Любое |
Есть |
|
V |
Любые |
Есть |
Есть |
Любые |
Любое |
Любое |
Любая |
Любое |
Есть |
Данная тема выносится на обсуждение.
| Выложил | alsak |
| Опубликовано | 12.07.07 |
| Просмотров | 13229 |
| Рубрика | Методика | Решение задач |
| Тема | Без тем |