Шмидт М.П. Статика. Решение статически неопределимых задач
-
0.0/5 оценка (0 голосов)
Шмидт М.П. Статика. Решение статически неопределимых задач // Фiзiка: праблемы выкладання. – 2006. – № 6. – С. 40-.
При решении задач о равновесии несвободного твёрдого тела реакции приложенных связей являются величинами, наперёд неизвестными. Число этих неизвестных зависит от числа и характера наложенных связей.
Задачи, в которых число неизвестных реакций связей больше числа уравнений равновесия, содержащих эти реакции, называются статически неопределимыми. Мы ограничимся случаем, когда число неизвестных реакций связей больше числа уравнений равновесия на единицу. Для однозначного решения такой задачи необходимо дополнительное уравнение. Это дополнительное уравнение можно получить, пользуясь представлениями об упругих деформациях элементов конструкции. Оно называется деформационным уравнением.
Решение статически неопределимых задач аналогично решению статически определимых. Отличием будет только то, что необходимо составить деформационное уравнение. Решение статически неопределимых задач рассмотрим на следующих примерах.
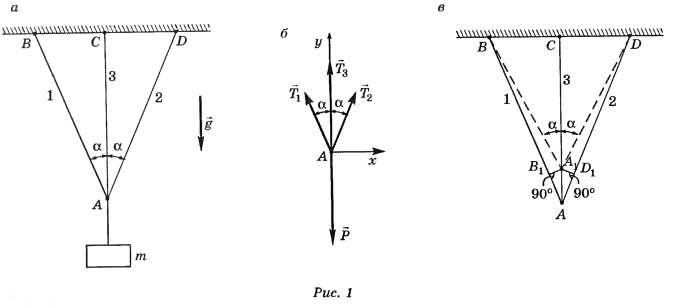
Задача 1. Груз массой m подвешен на одинаковых нитях, расположенных в одной плоскости (рис. 1, а). Крайние нити АВ и AD образуют угол а с вертикалью. Найдите силы растяжения (реакции) нитей АВ, АС и AD.
Решение. Рассмотрим равновесие узла А. На него действует одна активная сила — вес груза 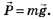 Освободим груз от связей (нитей), а их действие заменим реакциями
Освободим груз от связей (нитей), а их действие заменим реакциями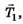
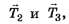 (рис. 1, б). Для равновесия узла А необходимо и достаточно, чтобы выполнялись условия
(рис. 1, б). Для равновесия узла А необходимо и достаточно, чтобы выполнялись условия
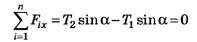
и
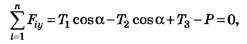
или
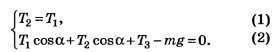
Система двух уравнений (1), (2) содержит три неизвестные: Т1 , Т2 и Т3. Для однозначного решения поставленной задачи дополним систему (1), (2) недостающим деформационным уравнением. Рассмотрим деформации нитей. Под действием силы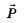 все три нити удлинятся и точка А опустится (рис. 1, в). Так как силы натяжения Т1 и Т2 равны между собой, то при равных длинах нитей их удлинения ∆l1 и ∆l2 будут одинаковы, точка А опустится по вертикали вниз. Пусть ∆l3= A1A — удлинение нити 3. Из рисунка 1, в находим, что удлинения нитей связаны соотношениями
все три нити удлинятся и точка А опустится (рис. 1, в). Так как силы натяжения Т1 и Т2 равны между собой, то при равных длинах нитей их удлинения ∆l1 и ∆l2 будут одинаковы, точка А опустится по вертикали вниз. Пусть ∆l3= A1A — удлинение нити 3. Из рисунка 1, в находим, что удлинения нитей связаны соотношениями
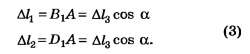
Считая, что деформации нитей упругие, согласно закону Гука имеем:
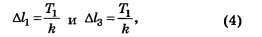
где k — коэффициент жёсткости нитей.
Соотношения (4) подставляем в (3), получим
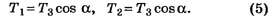
Подставляя (5) в (2), находим, что
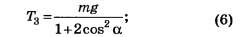
подставляя (6) в (5), получим
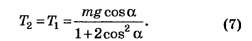
Если а=0, то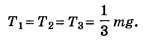 Этот факт очевиден.
Этот факт очевиден.
Ответ.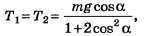
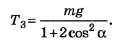
Задача 2 (6.1.16) [2]. Семь одинаковых зарядов q связаны друг с другом одинаковыми упругими нитями так, как показано на рисунке 2, а. Расстояние между ближайшими зарядами l. Определите силу натяжения (реакцию) каждой нити.
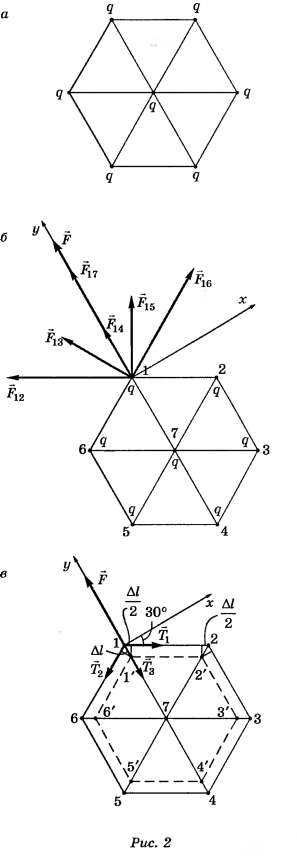
Решение. Из симметрии задачи следует, что на каждый заряд, находящийся в вершинах шестиугольника, со стороны остальных действует одинаковая по модулю радиальная сила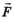 (рис. 2, б). Для определённости рассмотрим заряд, находящийся в вершине 1. На него действует сила
(рис. 2, б). Для определённости рассмотрим заряд, находящийся в вершине 1. На него действует сила

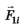 — сила, действующая на заряд, находящийся в вершине 1, со стороны заряда, находящегося в i-й точке (i = 2, 3, 4, 5, 6, 7).
— сила, действующая на заряд, находящийся в вершине 1, со стороны заряда, находящегося в i-й точке (i = 2, 3, 4, 5, 6, 7).
По закону Кулона
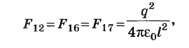
где Ɛ0 — электрическая постоянная,
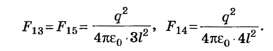
Проецируя (1) на оси х и у, получим
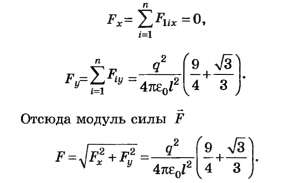
Рассмотрим равновесие заряда в вершине 1. На него действует активная сила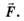 Освободим заряд от связей (нитей), а их действие<заменим реакциями
Освободим заряд от связей (нитей), а их действие<заменим реакциями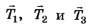 (рис. 1, в). Для равновесия заряда необходимо и достаточно, чтобы выполнялись условия
(рис. 1, в). Для равновесия заряда необходимо и достаточно, чтобы выполнялись условия
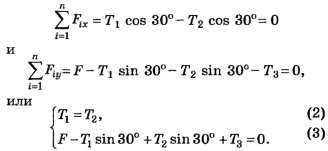
Система двух уравнений (2), (3) содержит три неизвестные: T1 , Т2 и Т3. Дополним систему (2), (3) деформационным уравнением. Под действием сил F, приложенных к каждому заряду в вершинах шестиугольника, нити удлинятся (рис. 2, в). Как видно из рисунка 2, в, все нити, радиальные и боковые, удлинятся на одну и ту же величину ∆l . Считая, что деформации нитей упругие, согласно закону Гука имеем:
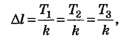
откуда следует, что
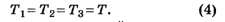
Силы натяжения всех нитей одинаковы.
С учётом (4) равенство (3) запишется
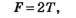
откуда
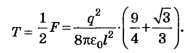
Ответ. Силы натяжения всех нитей одинаковы: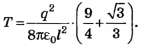
Задача 3 (2.8.38) [2]. Однородная балка длиной l висит на четырёх одинаковых канатах, прикреплённых на расстоянии l/3 друг от друга (рис. 3, а). Канат А удаляют. Для уменьшения опасности разрыва канатов предлагают удалить ещё и канат D. Разумное ли это предложение?
Решение. 1. Если балка висит на четырёх канатах, то силы натяжения всех канатов будут одинаковы: TA=TB=TC=TD= 0,25 mg.
2. Удалим канат А и рассмотрим равновесие балки в этом случае. На балку действует одна активная сила — сила тяжести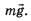 Освободим балку от связей (канатов), а их действие заменим реакциями
Освободим балку от связей (канатов), а их действие заменим реакциями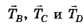 . Для равновесия балки необходимо и достаточно, чтобы выполнялись условия
. Для равновесия балки необходимо и достаточно, чтобы выполнялись условия
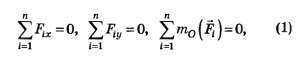
Так как на балку действуют вертикальные силы, то первое уравнение (1) выполняется. Составим ещё два уравнения:
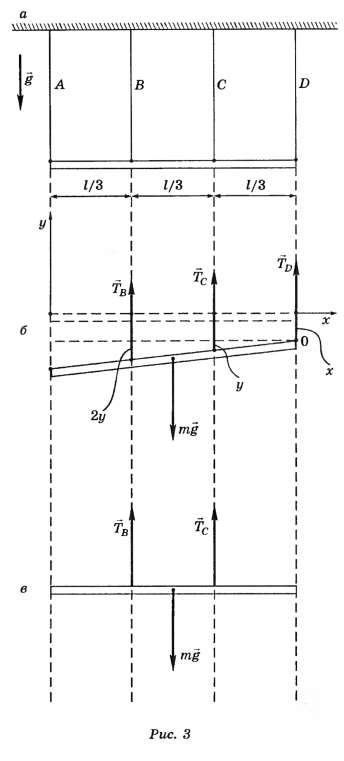
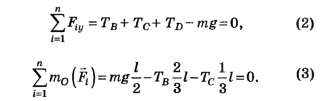
Полученные два уравнения содержат три неизвестные (массу балки m считаем известной). Дополним систему (2), (3) недостающим деформационным уравнением. Рассмотрим деформации канатов. Пусть канат D удлинится на величину ∆lD=x, тогда, как видно из рисунка 3, в, канат С удлинится на ∆lC=х+у, а канат В — на ∆lB=х+2у.
Согласно закону Гука
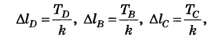
где k — коэффициент жёсткости канатов, или
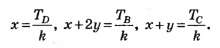
Из последних равенств следует, что деформационное уравнение имеет вид
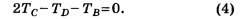
Из уравнений (2), (3) и (4) находим
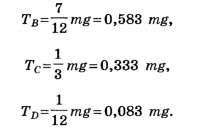
3. При удалении двух канатов А и D сила натяжения оставшихся канатов будет одинаковой:
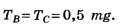
Так как 0,5 mg< 0,583 mg, то предложение удалить канат D при предварительном удалении каната А является достойным внимания.
1. Добронравов, В. В. Курс теоретической механики / В. В. Добронравов, Н. Н. Никитин, A. Л. Дворников. — М. : Высшая школа, 1966.
2. Воробьёв, И. И. Задачи по физике / И. И. Воробьёв [и др.]. — М. : Наука, 1988.
| Выложил | |
| Опубликовано | 01.08.16 |
| Просмотров | 11754 |
| Рубрика | Решение задач |
| Тема | Статика |