Слободянюк А.И. О динамическом равновесии
Слободянюк А.И. О динамическом равновесии // Фiзiка: праблемы выкладання. – 2001. – № 2. – С. 116-119.
Анализируются пять случаев динамического равновесия: 1) тело падает в воздухе; 2) насыщенный пар; 3) последовательное соединение двух проводников одинакового сечения, но с разными удельными сопротивлениями; 4) изотермическое расширение идеального газа; 5) катушка индуктивности в цепи переменного тока.
Во многих физических явлениях мы встречаемся с таким явлением, как установление динамического равновесия. Приведу несколько примеров на эту тему.
1. Тело падает в воздухе. По прошествии некоторого времени сила тяжести оказывается уравновешенной силой сопротивления воздуха, зависящей от скорости (рис. 1). Далее движение тела будет равномерным, т.е. с постоянной скоростью.
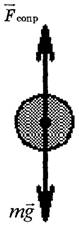
Рис. 1.
2. Если закрытый сосуд частично заполнен водой и поддерживается при постоянной температуре, то через некоторый промежуток времени пар над жидкостью придет в равновесие с жидкостью – количество молекул, вылетающих из жидкости, будет равно количеству молекул, возвращающихся из пара в жидкость.
3. Два проводника одинакового сечения, но с разными удельными сопротивлениями соединены последовательно. Через систему начинают пропускать электрический ток. Через некоторый интервал времени силы токов в проводниках станут равными (рис. 2). Действительно, в начальный момент времени сила тока будет больше в том проводнике, у которого сопротивление меньше. Из-за разности токов на границе раздела возникает электрический заряд, который увеличивает напряженность электрического поля (следовательно, и силу тока) в одном проводнике и уменьшает в другом. Этот процесс будет продолжаться до тех пор, пока силы токов не сравняются, в этом случае заряд на границе будет оставаться неизменным.
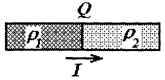
Рис. 2.
Во всех этих ситуациях динамическое равновесие является устойчивым, так как нарушение равновесия приведет к появлению причин, которые вернут систему в прежнее состояние динамического равновесия. Так, например, в первом примере, если скорость установившегося движения тела случайно уменьшится, то сила тяжести превысит силу сопротивления, и скорость шарика начнет возрастать, она достигнет прежнего равновесного значения. При случайном увеличении скорости сила сопротивления станет больше силы тяжести, поэтому скорость начнет уменьшаться. Аналогично можно показать устойчивость динамического равновесия в остальных примерах.
Отмечу существенное для дальнейшего общее свойство систем, для которых возможно состояние динамического равновесия – необходим некоторый промежуток времени как для установления равновесия, так и для возвращения системы в состояние равновесия после случайного отступления от него. Более того, в любом случае можно указать причины и их характеристики, которые приводят к наличию этого временного промежутка. Так, в первом примере – это инерционность падающего тела, т.е. его масса.
Рассмотрим еще несколько более сложных примеров.
4. При изотермическом расширении идеальный газ совершает работу, но его внутренняя энергия не изменяется. Понятно, что газ совершает работу за счет внешнего источника теплоты – нагревателя, температура которого равна температуре газа. Поэтому мощность потока теплоты от нагревателя равна мощности механической работы, совершаемой газом. Так обычно мы объясняем этот процесс. Однако возникает законный вопрос: почему при равенстве температур газа и нагревателя теплота перетекает от нагревателя к газу, а не наоборот? Конечно, для теплопередачи должна существовать разность температур между телами. Поэтому мы вынуждены признать, что в рассматриваемом примере температура газа должна быть немного меньше температуры нагревателя. Какие физические факторы могут обеспечить наличие этой разности – конечность времени теплопередачи, времени установления термодинамического равновесия внутри газа, незначительное понижение температуры газа непосредственно в области расширения и т.д.? При количественном описании процесса расширения мы пренебрегаем этими факторами (они действительно вносят весьма малые поправки в численные результаты), однако именно они определяют возможность существования данного процесса и его направление. Нетрудно также показать, что данный процесс также является динамически устойчивым, – например, при незначительном случайном увеличении температуры газа уменьшается приток теплоты, поэтому происходит понижение температуры газа при совершении работы. Можно также говорить о наличии времени установления рассматриваемого равновесия.
5. Катушка индуктивности включена в цепь переменного тока. При расчете такого участка цепи мы полагаем, что напряжение на катушке равно ЭДС самоиндукции. Исходя из этого положения, мы выводим все известные соотношения по поводу силы тока, сдвига фаз между током и напряжением и т.д. Однако опять возвращаемся к нашему основному вопросу: если внешнее напряжение равно ЭДС самоиндукции, то напряженность внешнего электрического поля уравновешивается напряженностью вихревого электрического поля, возникающего вследствие явления электромагнитной индукции. Что же в этом случае определяет направление электрического тока? Здесь мы опять встречаемся с динамическим равновесием – в начальный момент времени (при подключении источника) напряжение превышает ЭДС самоиндукции, в дальнейшем наступает равновесие, которое также является устойчивым (можете показать это самостоятельно). Теперь обсудим причины, которые приводят к тому, что ЭДС самоиндукции может быть меньше внешнего напряжения. Основная из них, конечно, – электрическое сопротивление катушки. Строго говоря, уравнение закона Ома для катушки формулируется следующим образом: разность между внешним сопротивлением и ЭДС самоиндукции равна произведению силы тока на сопротивление катушки. Как и в предыдущем примере, при расчетах можно пренебречь сопротивлением, но при этом фактически теряется физическая сущность явления.
Наконец-то мы подошли к ответу на поставленный вопрос о задачах со сверхпроводниками в магнитном поле.
В очередной раз можно порассуждать о динамическом равновесии и его устойчивости. Однако какова причина, которая может привести к наличию пусть бесконечно малой разности между ЭДС индукции и ЭДС самоиндукции. Привлечь электрическое сопротивление в случае сверхпроводников нельзя – для последних оно равно нулю в математическом смысле! Причина внутри самого сверхпроводника – инертность электронов. Действительно, процесс установления тока (как в обычном проводнике, так и в сверхпроводнике) сводится к достижению электронами некоторой установившейся скорости. В обычном проводнике на электрон, помимо электрической силы, действует тормозящая сила, зависящая от его скорости, поэтому этот вид равновесия аналогичен рассмотренному падению тела. В случае сверхпроводника в качестве «тормозящей» силы выступает вихревое электрическое поле (нечто, отдаленно напоминающее так называемую магнитную вязкость). Можно показать, что более строгое решение рассмотренной задачи включает малую добавку к индуктивности кольца, пропорциональную массе электрона. Понятно, что эта добавка чрезвычайно мала, но без нее нельзя объяснить возникновения тока и его направление.
В заключение отмечу, что при желании все приведенные рассуждения можно перевести на язык достаточно строгих математических формул.
| Выложил | alsak |
| Опубликовано | 30.12.07 |
| Просмотров | 12995 |
| Рубрика | Решение задач |
| Тема | Постоянный ток Магнитное поле Динамика |