Слободянюк А.И., Маркович Л.Г. Олимпиада по физике стран СНГ (отборочный тур в РБ)
Слободянюк А. И., Маркович Л. Г. Олимпиада по физике стран СНГ (отборочный тур в Республике Беларусь) // Фiзiка: праблемы выкладання. – 2009. – № 3. – С. 41–51
Задача 1. "Славянский экспресс"
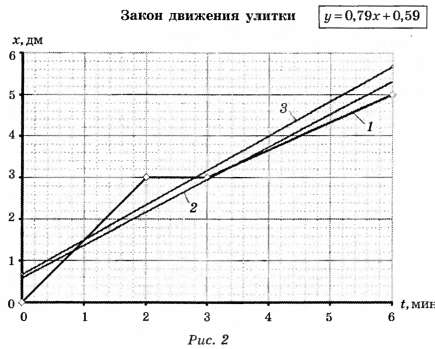
1.1. На графике приведена зависимость координаты х улитки, движущейся прямолинейно, от времени t.
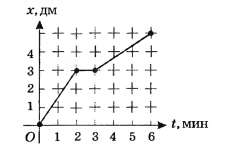
1.1.1. Постройте графики зависимостей скорости v улитки от времени t и от пройденного пути s.
1.1.2. Найдите среднюю скорость движения улитки за промежутки времени t1=3,0 мин, t2=6,0 мин от начала движения.
1.1.3. Аппроксимируйте движение улитки законом равномерного движения на всём временном интервале оптимальным образом. Критерий оптимальности сформулируйте самостоятельно. Запишите уравнение этого закона движения. Укажите максимальную погрешность определения координаты улитки по вашей аппроксимации.
1.2. В таблице приведён график движения славянского экспресса "Минск—Москва". Время прибытия и отправления местное.
|
№ п/п |
Наименование станции |
Время прибытия |
Время стоянки, мин |
Время отправления, мин |
Расстояние, км |
|
1 |
Минск-Пасс. |
— |
— |
18.28 |
0 |
|
2 |
Смолевичи |
19.02 |
2 |
19.04 |
39 |
|
3 |
Жодино |
19.22 |
2 |
19.24 |
61 |
|
4 |
Борисов |
19.40 |
3 |
19.43 |
79 |
|
5 |
Крупки |
20.12 |
8 |
20.20 |
119 |
|
6 |
Толочин |
20.56 |
2 |
20.58 |
169 |
|
7 |
Орша-Центральная |
21.31 |
14 |
21.45 |
212 |
|
8 |
Осиновка |
22.07 |
2 |
22.09 |
238 |
|
9 |
Смоленск Центр. |
0.07 |
5 |
0.12 |
331 |
|
10 |
Вязьма |
2.21 |
22 |
2.43 |
507 |
|
11 |
Москва Бел. |
6.00 |
— |
— |
750 |
1.2.1. Постройте график закона движения экспресса.
1.2.2. Определите среднюю скорость экспресса за всё время движения.
1.2.3. Аппроксимируйте движение поезда законом равномерного движения по методу наименьших квадратов. Определите максимальную ошибку расчёта времени отправления поезда по вашей аппроксимации.
Примечание. Аппроксимация означает приближение.
Задача 2. "Звезда Востока"
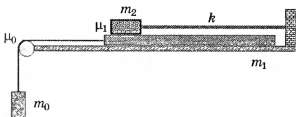
На гладкой горизонтальной поверхности стола покоится длинная доска массой m1 на которой расположен брусок массой m2. Брусок прикреплён к неподвижной вертикальной стенке лёгкой длинной пружиной жёсткостью k. Коэффициент трения между доской и бруском равен μ1. К доске привязывают лёгкую нерастяжимую нить, которую перебрасывают через цилиндрический стержень, закреплённый на торце стола. Коэффициент трения между нитью и поверхностью стержня равен μ0. К другому концу нити прикрепляют груз массой m0. Сначала этот груз удерживают так, что нить оказывается натянутой, а пружинка недеформированной. Затем груз отпускают без начальной скорости, и он начинает опускаться.
2.1. Если нить скользит по боковой поверхности цилиндра, то модули сил натяжения нити с разных сторон от цилиндра различаются. Покажите, что модули этих сил связаны соотношением
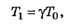
где λ— постоянный коэффициент. Выразите значение этого коэффициента через значение коэффициента трения μ0
2.2. Найдите закон движения доски x(t) от начала движения до того момента времени, когда брусок начнёт проскальзывать по доске.
2.3. При каком минимальном значении коэффициента трения μ1=μ1* брусок не будет проскальзывать по доске во время ее движения?
2.4. Пусть μ1=μ1*.Определите, в какой момент времени после начала движения доски начнётся проскальзывание бруска.
Задача 3. "Держи меня соломинка..."
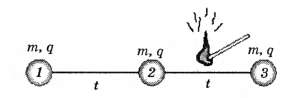
Три одинаковых маленьких шарика массой m=1,3г и зарядом q=2,5 мкКл каждый соединены двумя лёгкими непроводящими нитями длиной l=20см каждая. Система находится в равновесии. Определите силу натяжения нитей в положении равновесия. Правую нить пережигают. Определите скорости vi всех шариков "на бесконечности".
После того как третий шарик удалился на значительное расстояние, перегорает нить между первым и вторым шариками. Определите скорости шариков 1 и 2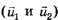 через достаточно большой промежуток времени после перегорания второй нити.
через достаточно большой промежуток времени после перегорания второй нити.
Задача 4. "Световой разгон"
4.1. Группа спортсменов выполняет следующее упражнение. Спортсмены выстраиваются в колонну на равном расстоянии l0 друг от друга. На таком же расстоянии l0 от первого спортсмена располагается тренерский автомобиль.
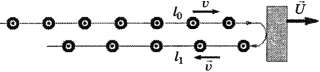
По команде автомобиль и все спортсмены начинают одновременно двигаться в одном направлении, автомобиль с постоянной скоростью U, спортсмены с одинаковыми и постоянными скоростями v (v>U). Спортсмен, догоняющий автомобиль, касается его и поворачивает обратно, продолжая бег с прежней скоростью V.
4.1.1. Постройте графики законов движения автомобиля и первых трёх спортсменов. Считайте, что в момент старта автомобиль находится в начале координат. Дайте аналитическое выражение (т.е. формулу) для зависимости координаты k-того спортсмена (нумерация спортсменов начинается от автомобиля) от времени xk(t).
4.1.2. Чему будет равна дистанция между спортсменами l1 после их поворота?
4.2. Фотон частотой v0 падает нормально на плоское зеркальце массой m, движущееся со скоростью v.
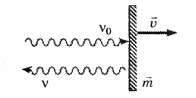
4.2.1. Чему будет равна частота отражённого фотона, если изменением скорости зеркальца пренебречь?
4.2.2. Считая, что v<c (с — скорость света), выразите относительное изменение частоты фотона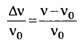 как линейную функцию отношения
как линейную функцию отношения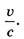 Массу зеркальца считайте бесконечно большой.
Массу зеркальца считайте бесконечно большой.
4.2.3. Оцените поправку к относительному изменению частоты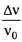 , вызванную конечностью массы зеркальца. Для описания движения зеркальца можно использовать формулы классической механики.
, вызванную конечностью массы зеркальца. Для описания движения зеркальца можно использовать формулы классической механики.
4.3. Небольшая пылинка массой m, на задней стороне которой находится плоская зеркальная поверхность площадью S, освещается мощным параллельным световым потоком интенсивностью I0, который полностью отражается от пылинки в противоположном направлении.
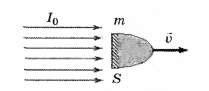
4.3.1. Найдите силу светового давления на пылинку в момент времени, когда её скорость равна v.
4.3.2. Найдите зависимость скорости пылинки от времени v(t), считая, что в начальный момент времени она покоилась.
4.3.3. Оцените, через какой промежуток времени пылинка достигнет скорости, равной 0,10 с, если m=1,0мг, S=0,10mm2,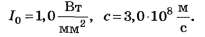
Возможные решения задач и разбалловки для их проверки
Задача 1. "Славянский экспресс"
1.1.
1.1.1. Графики зависимостей скорости улитки v от времени t и от пройденного пути s хоть и незначительно, но различаются (рис. 1, а, б).
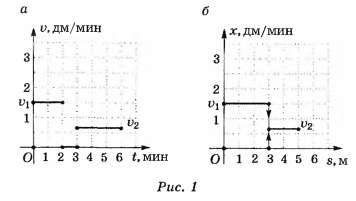
Значения скоростей на графиках равны соответственно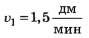 и
и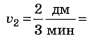
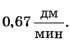
1.1.2. При вычислении средних скоростей улитки следует воспользоваться определением средней скорости как отношения всего пройденного пути ко всему времени движения.
Пользуясь графиком, получим, что за промежуток времени t=3,0 мин средняя скорость
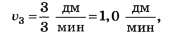
а за промежуток времени t2=6,0мин она составит
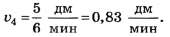
1.1.3. Для проведения аппроксимации функции 1 движения улитки (рис. 2) можно воспользоваться методом наименьших квадратов (МНК), методом минимакса или даже методом обработки зависимости "на глаз". Все методы приводят к достаточно близким результатам.
Так, при обработке по МНК (прямая 2 на рисунке 2) получим, что скорость (угловой коэффициент прямой)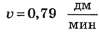 , свободный член x0=0,59 дм.
, свободный член x0=0,59 дм.
Максимальная погрешность определения координаты улитки по линейной аппроксимации достигается в одной из "вершин" графика, т.е. в одной из точек его излома. В нашем случае ∆xmax=0,59 дм.
1.2.
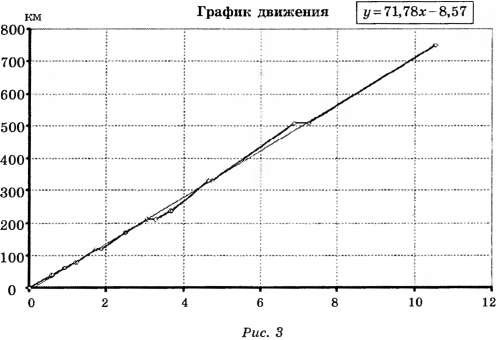
1.2.1. График движения экспресса показан на рисунке 3.
1.2.2. При вычислении средней скорости движения славянского экспресса из таблицы следует найти всё время его движения (не забыть про сдвиг на час по времени!). Это составит t=10ч 32 мин=10,5 ч. Соответственно средняя скорость экспресса за всё время движения.
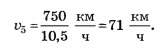
1.2.3. Для аппроксимации закона движения поезда прямой линией на рисунке 3 использован метод МНК. Согласно полученной аппроксимации скорость поезда (угловой коэффициент прямой)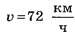 . а максимальная ошибка расчёта времени отправления соответствует точке максимальной стоянки в Вязьме и составляет ∆t = 16 мин.
. а максимальная ошибка расчёта времени отправления соответствует точке максимальной стоянки в Вязьме и составляет ∆t = 16 мин.
Схема оценивания
|
Пункт |
Подпункт |
Содержание |
Всего |
Балл |
Оценка |
|
|
1.1 |
Улитка |
19 |
||||
|
1.1.1 |
Зависимость скорости от времени — все точки нанесены верно |
2 |
||||
|
Зависимость скорости от координаты — все точки нанесены верно |
3 |
|||||
|
1.1.2 |
Средняя скорость — 1 дм/мин — 0,83 дм/мин |
1 1 |
||||
|
1.1.3 |
Формулировка критерия оптимальности (МНК, минимакс, другое разумное) |
3 |
||||
|
Метод расчёта МНК, другой разумный ("на глаз") |
2 (1) |
|||||
|
Уравнение движения — формула закона х = a + vt — численные значения МНК a=0,5-0,7; v=0,7-0,9 (минимакс, "на глаз") a=0,6-0,8; v=0,7 - 0,9 |
1 2+1 (2+1) |
|||||
|
Максимальное отклонение (обосновано) D=0,67-0,85 (D=0,85 — 0,95) |
2 (1) |
|||||
|
1.2 |
Славянский экспресс |
16 |
||||
|
|
1.2.1 |
График — оси оцифрованы и подписаны — все точки нанесены верно — соединены отрезками прямых |
1 3 1 |
|||
|
|
1.2.2 |
— средняя скорость 71 км/час |
2 |
|||
|
|
1.2.3 |
Аппроксимация — указан критерий минимизации |
2 |
|||
| — численные значения параметров
v=71-73 км/ч; a= -7,5--9,5 км <v> =70-74 км/ч; a = -6,5--10,5 км) |
4 (2) |
|||||
|
|
— максимальная ошибка времени 0.25—0,30 ч (0.25—0.35 ч) |
3 (1) |
||||
|
Всего за задачу |
35 |
|||||
Задача 2. "Звезда Востока"
2.1. Выделим на нити, скользящей по поверхности цилиндра, малый участок, видимый из центра под углом Так как масса нити пренебрежимо мала, то сумма сил, действующих на этот участок, равна нулю. Запишем это условие в проекциях на радиальное и касательное направление к выделенному участку:
Так как масса нити пренебрежимо мала, то сумма сил, действующих на этот участок, равна нулю. Запишем это условие в проекциях на радиальное и касательное направление к выделенному участку:
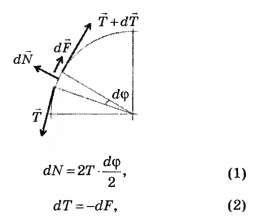
гдеdF=μ0dN — сила трения.
Из этих выражений следует, что
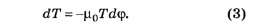
Решение этого уравнения, с учётом начального условия, имеет вид
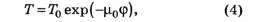
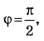 , поэтому
, поэтому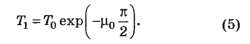
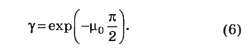
2.2. Запишем очевидные уравнения второго закона Ньютона (до момента начала проскальзывания бруска):
■ для груза:
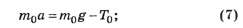
■ для доски:
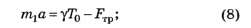
■ для бруска:
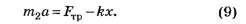
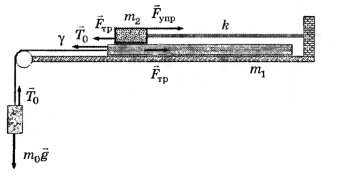
Из этих уравнений получаем уравнение
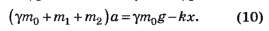
Это уравнение гармонических колебаний, которое можно переписать в виде
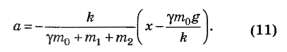
Решение этого уравнения с учётом начальных условий имеет вид
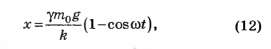
где 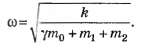
2.3. Из уравнения (9) выразим силу тренияFтр=m2α+kx и подставим значения для координаты и ускорения бруска:
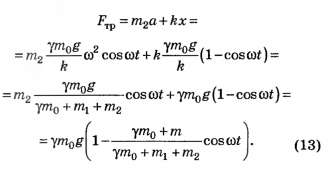
Максимальное значение эта сила принимает при cos(ωt)=-1:
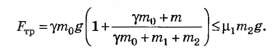
Отсюда определяем
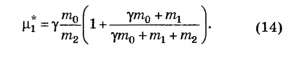
2.4. В выражение (13) подставляем максимальное значение силы трения покоя и определяем время движения до начала проскальзывания:
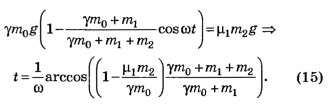
|
Пункт |
Подпункт |
Содержание |
Всего |
Балл |
Оценка |
|
2.1 |
Силы натяжения нити |
7 |
|||
|
Выделение малой части |
1 |
||||
|
Рисунок сил |
1 |
||||
|
Уравнения в проекциях (1) — (2) |
2 |
||||
|
Уравнение (3) |
1 |
||||
|
Его решение (4) |
1 |
||||
|
Выражение для коэффициента (6) |
1 |
||||
|
2.2 |
Закон движения |
11 |
|||
|
Рисунок сил |
1 |
||||
|
Уравнения (7) — (9) |
3 |
||||
|
Уравнение(11) |
2 |
||||
|
Есть уравнение гармонических колебаний |
2 |
||||
|
Закон движения (12): частота, амплитуда, начальные условия, конечное выражение |
4 |
||||
|
2.3 |
Минимальный коэффициент трения |
8 |
|||
|
Выражение для силы трения (13) |
4 |
||||
|
Максимальное значение для силы трения (покоя и требуемое из уравнения) |
2 |
||||
|
Выражение для коэффициента трения (14) |
2 |
||||
|
. 2.4 |
Время до начала проскальзывания |
4 |
|||
|
Уравнение (15) |
2 |
||||
|
Его решение |
2 |
||||
|
Всего за задачу |
30 |
||||
Задача 3. "Держи меня соломинка..."
В положении равновесия сумма сил, действующих на любой шарик системы, должна быть равна нулю.
Соответственно первое условие равновесия для крайнего (например, левого) шарика системы примет вид (рис. 4)
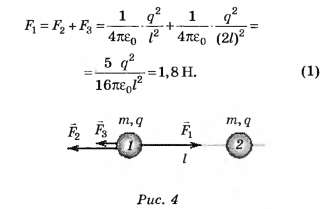
Результат (1) округляем до двух значащих цифр, поскольку все данные условия содержат по две значащие цифры. Напомним, что согласно правилам приближённых вычислений количество значащих цифр в ответе определяется по наименьшему количеству значащих цифр у численных данных, приведённых в условии задачи.
После пережигания нити связанные шарики 1 и 2 под действием сил Кулона начнут двигаться влево, а шарик 3, согласно III закону Ньютона, — вправо (рис. 5).
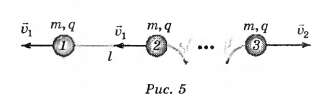
При этом кинетическая энергия системы будет увеличиваться за счёт убыли потенциальной энергии электростатического взаимодействия зарядов.
Поскольку на бесконечности потенциальная энергия взаимодействия шариков 1 и 2 с шариком 3 пренебрежимо мала, то согласно закону сохранения энергии можем записать
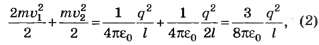
где v1 и v2 — искомые скорости левого (центрального) и правого шариков соответственно.
Поскольку система взаимодействующих шариков замкнута, то согласно закону сохранения импульса получим ещё одно уравнение

Решая систему (2) — (3), получим
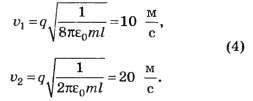
Если на бесконечности перегорает и вторая нить, то освобождается дополнительная потенциальная энергия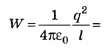 0,281 Дж, которая пойдёт на увеличение кинетических энергий (скоростей) шариков 1 и 2.
0,281 Дж, которая пойдёт на увеличение кинетических энергий (скоростей) шариков 1 и 2.
В соответствие с законами сохранения импульса и энергии для искомых скоростей шариков u1 и u2 (рис. 6) через достаточно большой промежуток времени получаем систему уравнений
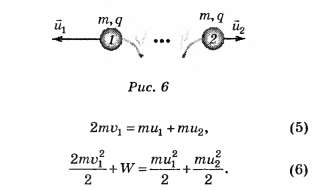
Решение системы (5)—(6) даёт
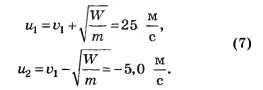
Заметим, что, как следует из (7), правый шарик 2 после разрыва второй нити начнёт движение в противоположном направлении (см. рис. 6), поскольку проекция его скорости u2 отрицательна.
Убедитесь самостоятельно, что по закону сохранения импульса суммарный импульс системы (т.е. всех трёх шариков) после разрывов всех нитей остаётся равным нулю.
Схема оценивания
|
Пункт |
Подпункт |
Содержание |
Всего |
Балл |
Оценка |
|
1.1 |
15 |
||||
|
1 |
Расчёт силы натяжения в равновесии |
1 |
|||
|
Первый разрыв |
|||||
|
2 |
Запись закона сохранения импульса |
1 |
|||
|
Запись закона сохранения энергии |
i |
||||
|
Получение итоговых выражений |
2 |
||||
|
Расчёт (значащие цифры) |
3 |
||||
|
Второй разрыв |
|||||
|
Запись закона сохранения импульса |
1 |
||||
|
Запись закона сохранения энергии |
1 |
||||
|
Получение итоговых выражений |
2 |
||||
|
Расчёт (значащие цифры) |
3 |
||||
|
Всего за задачу |
15 |
||||
Задача 4. "Световой разгон"
4.1. В соответствии с условием задачи запишем законы движения
■ автомобиля

■ k-того спортсмена (до "отражения" от автомобиля)

Приравнивая эти координаты, найдём время и координату "отражения" k-того спортсмена:
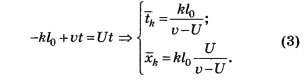
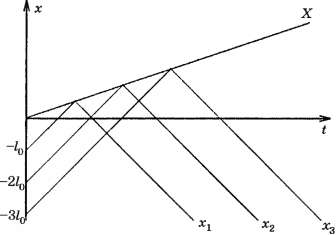
Теперь можно записать уравнение закона движения после "отражения":
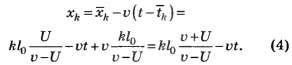
Графики законов движения показаны на рисунке.
Расстояние между соседними бегунами после "отражения"
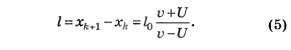
4.2. Аналогом длины волны и её изменения может служить расстояние между бегунами в предыдущем пункте, поэтому изменение длины волны описывается формулой, аналогичной формуле (5):
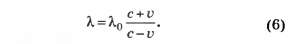
Так как частота волны обратно пропорциональна длине волны, то частоты фотона до и после отражения связаны соотношением
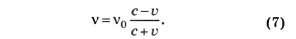
При малых скоростях зеркала формула (7) упрощается:
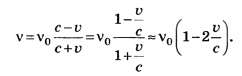
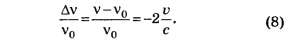
Для учёта изменения скорости зеркальца при отражении фотона следует записать уравнения закона сохранения импульса и энергии при отражении фотона:
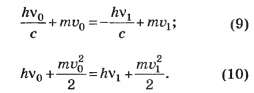
Перепишем эти уравнения в виде
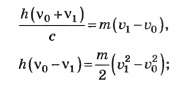
разделим одно на другое, выразим скорость после отражения
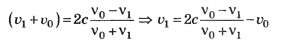
и подставим в уравнение (9):
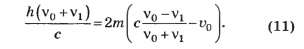
Строго говоря, это уравнение является квадратным относительно частоты фотона после отражения. Но в нём легко можно заметить малый параметр. Используем соотношение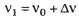 и перепишем уравнение (11) в виде
и перепишем уравнение (11) в виде

Очевидно, что величина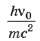 крайне мала, поэтому в последнем уравнении можно оставить только малые величины первого порядка:
крайне мала, поэтому в последнем уравнении можно оставить только малые величины первого порядка:
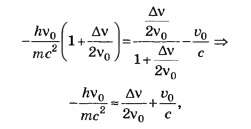
Откуда следует, что 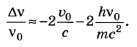
Таким образом, искомая поправка равна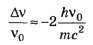 и мала настолько, что ею заведомо можно пренебрегать (даже если зеркальце состоит из одного электрона).
и мала настолько, что ею заведомо можно пренебрегать (даже если зеркальце состоит из одного электрона).
4.3. Прежде всего отметим, что мощность светового потока, падающего на движущееся зеркало, меньше, чем мощность потока через неподвижную площадку: свет ещё должен "догнать" зеркало. Легко показать, что мощность потока, попадающего на движущееся зеркало:
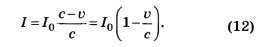
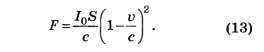
Уравнение второго закона Ньютона для зеркала имеет вид
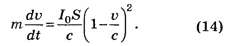
Это уравнение решается методом разделения переменных:
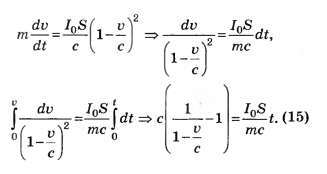
Окончательно находим
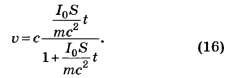
Для расчёта времени разгона удобно воспользоваться формулой (15):
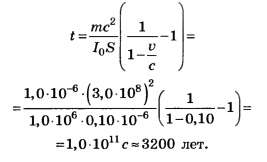
Схема оценивания
|
Пункт |
Подпункт |
Содержание |
Всего |
Балл |
Оценка |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
4.1 |
Спортсмены |
10 |
|||
|
Закон движения автомобиля |
1 |
||||
|
Закон движения бегуна до встречи (2) |
1 |
||||
|
Время и место встречи (3) |
2 |
||||
|
Закон движения (4) |
2 |
||||
|
График (наклоны графиков, начальные смещения) |
2 |
||||
|
Расстояния после поворота (5) |
2 |
||||
|
4.2 |
Изменение частоты |
15 |
|||
|
4.2.1 |
Применение формулы (5) |
2 |
|||
|
Выражение для частот (7) |
1 |
||||
|
4.2.2 |
Вывод формулы (8) |
2 |
|||
|
4.2.3 |
Использование законов сохранения |
2 |
|||
|
Импульс и энергия фотона |
1 |
||||
|
Уравнения (9)—(10) |
2 |
||||
|
Решение уравнений приближённое (точное) |
3(2) |
||||
|
Выражение для поправки |
2 |
||||
|
4.3 |
Разгон пылинки |
20 |
|||
|
4.3.1 |
Сила, как изменение импульса |
1 |
|||
|
Связь импульса с интенсивностью |
1 |
||||
|
Учёт изменения мощности потока |
2 |
||||
|
Учёт изменения импульса фотона при отражении |
2 |
||||
|
Выражение для силы (13) |
2 |
||||
|
4.3.2 |
Уравнение закона Ньютона |
1 |
|||
|
Уравнение(14) |
1 |
||||
|
Решение уравнения (14) |
2 |
||||
|
Окончательная формула (16) |
2 |
||||
|
4.3.4 |
Расчётная формула для времени |
2 |
|||
|
Подстановка значений в СИ |
1 |
||||
|
Численное значение (2 значащие цифры) |
3 |
||||
|
Всего за задачу |
45 |
||||
Результаты отборочного тура в Республике Беларусь олимпиады стран СНГ (2008—2009 гг.)
|
Фамилия, имя |
Класс |
Задание 1 |
Задание 2 |
Задание 3 |
Задание 4 |
Сумма баллов |
|
Митьковец Анна |
11 |
29 |
21 |
14 |
19 |
83 |
|
Горлач Максим |
10 |
25 |
30 |
12 |
0 |
67 |
|
Лесневский Георгий |
11 |
22 |
12 |
12 |
20 |
66 |
|
Гущин Михаил |
11 |
17 |
9 |
9 |
23 |
58 |
|
Плехова Татьяна |
10 |
18 |
12 |
9 |
17 |
56 |
|
Соболь Сергей |
11 |
15 |
20 |
8 |
13 |
56 |
|
Каргин Игорь |
10 |
21 |
12 |
13 |
8 |
54 |
|
Барабаш Мирослав |
10 |
17 |
12 |
10 |
12 |
51 |
|
Дашкевич Антон |
11 |
17 |
9 |
4 |
17 |
47 |
|
Рымарчик Игорь |
10 |
18 |
4 |
13 |
10 |
45 |
|
Парафенюк Николай |
10 |
19 |
1 |
14 |
10 |
44 |
|
Петруша Станислав |
11 |
14 |
1 |
12 |
14 |
41 |
|
Глушко Сергей |
10 |
15 |
6 |
9 |
8 |
38 |
|
Ледник Александр |
10 |
19 |
5 |
7 |
3 |
34 |
|
Ачаповский Андрей |
10 |
18 |
2 |
8 |
6 |
34 |
|
Куликов Николай |
10 |
19 |
1 |
4 |
5 |
29 |
| Выложил | alsak |
| Опубликовано | 07.03.12 |
| Просмотров | 6152 |
| Рубрика | Олимпиады |
| Тема | Без тем |