Слободянюк А.И. Подготовка школьной олимпиады по физике-08-5

Ежегодный цикл предметных олимпиад начинается с самого массового первого этапа — школьных олимпиад. Разработка заданий этого этапа возложена непосредственно на школьных учителей физики. В данной статье предлагается обсудить общие требования к олимпиадным задачам школьного этапа.

1.1. Соответствие действующим учебным программам и содержанию пройденного материала.

Этот тезис не вызывает возражений, но требует некоторых пояснений. Очевидно, что учебную программу не следует воспринимать слишком буквально. Большинство физичес­ких законов, изучаемых в школе, имеют многочисленные проявления в природных явлениях, по-разному используются в техни­ческих приложениях. В условиях дефицита учебного времени нет возможности рассмот реть ни уроках мною примеров, иллюстриру­ющих тот или иной физический закон, обычно дело ограничивается одним-двумя примерами. Но при составлении олимпиадных задач этот "пробел" может быть воспол­нен. Так, например, в курсе физики
удель­ная теплоёмкость вещества, как правило, рассматривается как величина постоянная.

Но в некоторых случаях она может изме­няться, и этот факт может быть положен в основу олимпиодной задачи.

Пример 1. Теплоёмкости тел могут за­висеть от температуры (например, при низ­ких температурах). Два одинаковых тела, удельные теплоёмкости которых зависят от температуры по закону

где с₀ и а — известные постоянные вели­чины, приведены в тепловой контакт. На­чальные температуры тел равны t₁ и t₂. Оп­ределите установившуюся температуру тел. Потерями теплоты пренебречь.

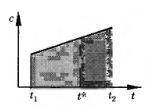
Решение данной задачи фактически сво­дится к пониманию того, что площадь под графиком зависимости теплоёмкости от тем­пературы с(t) есть количество переданной теплоты. Так как теплоёмкости тел одинако­вы, условию теплового баланса соответствует равенство площадей трапеций под графином от t₁ до установившейся температуры t* и от t* до t₂.

1.2.  Задача должна быть физически корректна.

К сожалению, многие составители подач грешат чрезмерной идеализацией, часто формулируют такие условия, которые никог­да не реализуются в действительности. Ти­пичным примером такой задачи может слу­жить следующее условие: "Шарик всплыва­ет в жидкости — сопротивлением воды пре­небречь"(!?). В указанной ситуации сила со­противления является во многом определяю­щей закон движения. Кстати, и задачах по­добного типа предполагается использование закона Архимеда, который, строго говоря, применим только для покоящихся в жидко­сти тел.

1.3.   При решении задачи необходимо глубокое понимание сущности используемых законов и формул.

Поясним данный тезис следующим при­мером. Хорошо известна формула для сопро­тивления проводника

В этой формуле самое важное понимать, что такое длина проводника, а что такое пло­щадь поперечного сечения. Рассмотрим та­кой вопрос: "Прямоугольный параллелепи­пед размерами 10x2,0x1,0 см изготовлен из
материала с удельным сопротивлением ρ=1,0 Ом·м. Чему равно сопротивлеиие про­водника?"  Эта задача не сформулирована до конца! Пока не указано (или не найдено) на­правление распространения тока, сопро­тивление не может быть найдено (Очень часто ученики считают, что длина - это тот размер, который "длиннее"). Вспом­ним: в приведённой формуле l — длина в направлении распространения тока, а S — площадь
сечения, перпендикулярного току.

Пример 2. Для не­прерывного нагревания во­ды используется следую­щая установка.

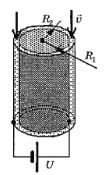
Вода мед­ленно прокачивается меж­ду двумя металлическими коаксиальными цилиндра­ми, радиусы которых рав­ны R₁ и R_2, причём рас­стояние между цилиндра­ми значительно меньше их радиусов. Длины ци­линдров одинаковы и рав­ны l. К цилиндрам приложено постоянное напряжение U. С какой скоростью V должна протекать вода между цилиндрами, чтобы она успела нагреться на Δt градусов? Плот­ность, удельное электрическое сопротивле­ние и удельную теплоёмкость воды считать известными. Потерями теплоты пренебречь.

Основная "изюминка" данной задачи за­ключается в умении правильно рассчитать электрическое сопротивление слоя воды между цилиндрами. Так как электрический ток протекает перпендикулярно поверхности  цилиндров, то "длина" проводиика в данном случае есть расстояние между цилиндрами

а площадь поперечного сечения есть площадь боковой поверхности

1.4. Олимпиадная задача, по возможно­сти, должна быть оригинальна и интересна.

Трудно перечислить все сборники задач по физике, да и в Интернете несложно най­ти сайты, посвященные олимпиадам. Но за многие года преподавания физики в различ­ных странах сложился определённый набор типовых задач: грузы на блоках, бруски на наклонных плоскостях, невесомые нити, иде­ально гладкие поверхности и т.д. Никто не отрицает необходимости обучения решению этих типовых задач, но... всё-таки олимпиадные задачи должны чем-то отличаться. В ок­ружающем нас мире вполне достоточно дви­жущихся тел, электрических цепей и при­боров, промышленных установок, оптичес­ких явлений...

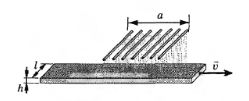
Пример 3. Из прокатного стана выходит длинная стальная лента шириной l=2.0 м и толщиной h =4.0 мм, находящаяся при температуре t₀=500°С.

Лента движется  с постоянной скоростью   V=0,50 м/с.  Для охлаждeния ленты её поливают водой, темпе­ратура которой равна t₀=20°С. Вода подает­ся через охлаждающую установку, состоя­щую из системы параллельных трубок с от­верстиями. Расстояние между крайними трубками равно а = 3,0 м. Какой объем воды каждую секунду должен проходить через ох­лаждающую установку, чтобы охладить лен­ту до температуры t = 100 °С?

Плотность стали плотность воды удельные теп­лоёмкости стали и воды соответственноудельная теплота испарения воды

Решение данной задачи сводится к пра­вильной записи уравнения теплового балан­са, но, согласитесь, эта задача гораздо инте­реснее, чем традиционная "брусок опускают в калориметр...".

1.5. Олимпиадная задача не должна быть перегружена математическими вы­кладками.

Отношения между "физикой" и "матема­тикой" достаточны своеобразны. Зачастую основные проблемы я решении физической задачи сводятся к необходимости проведения громоздких математических преобразова­ний. Часто эти расчёты и вычисления необ­ходимы — окружающий нас мир не так уж прост. Но физическая олимпиада призвана оценивать знание и понимание физики, поэтому обидно, когда красивые физические идеи оказываются "погребёнными" под стра­ницами математических выкладок. В такой ситуации имеет смысл до предела упростить физическую ситуацию, предложить упро­щенную до примитивизма модель
явления, но оставить основную физическую идею. В некоторых случаях математические осо­бенности решения неявно выявляют ориги­нальную физическую ситуацию.

Пример 4. Проводник из графита, со­противление которого зависит от температу­ры, подключили к источнику напряжения, величина которого равна U. Зависимость сопротивления проводника от температу­ры описывается формулой

где R₀, α — положительные постоянные вели­чины. t — температура проводника, изме­ренная в градусах Цельсия. Проводник нахо­дится в среде, температура которой поддер­живается постоянной и равной 0 ^оС. Мощ­ность теплоты Р, передаваемой проводником в среду, пропорциональна Δt разности тем­ператур проводника и среды

где β — положительный коэффициент.

Найдите зависимость установившейся температуры проводника от напряжения ис­точника, постройте примерный график этой зависимости.

Решение этой задачи также сводится к правильной записи уравнения теплового ба­ланса: в установившемся режиме мощность теплоты, выделяющейся при прохождении тока через проводник (которая определяется законом Джоуля—Ленца), равна мощности теплоты, отдаваемой проводником в окружа­ющую среду.

Это уравнение является квадратным отно­сительно неизвестной установившейся тем­пературы. В зависимости от приложенного напряжения Vданное уравнение имеет либо два, либо один корень, либо корней не име­ет. Важно теперь понять физический смысл этих возможных вариантов: если уравнение имеет два корня, то один из них надо отбро­сить (следует показать, что он неустойчив), если  же уравнение корней  не
имеет, это означает только то, что в такой ситуации ус­тановление теплового равновесия невозмож­но — температура проводника будет возрас­тать до тех пор пока он не перегорит.

Последний пример иллюстрирует ещё одну особенность олимпиадных задач — же­лательно внимательно анализировать полу­ченные результаты. Несмотря на то что "служанка" (т.е. математика) всегда посту­пает правильно, итоги её работы могут не удовлетворить "хозяйку" (т.е. физику). Ука­жем также, что во многих случаях при ре­шении задач следует пользоваться прибли­жёнными математическими методами - это может
существенно облегчить задачу.

1.6. Комплект заданий должен быть раз­нообразным — включать различные разде­лы изученного курса.

Число задач, входящих в комплект зада­ний, ограничено временем проведения, по­этому не может быть слишком большим (не более пяти).  Трудно составить комплект, за­дачи которого "покрывали" бы все изучен­ные
разделы, но ещё хуже, если все задачи посвящены одному разделу (скажем, меха­нике). Очень интересны так называемые комплексные задачи, решение которых тре­бует применения законов и формул из раз­личных тем курса физики. Во-первых, они расширяют диапазон используемого матери­ала, во-вторых, показывают, насколько уче­ник разбирается в сущности изучаемого фи­зическою явления, насколько он мыслит самостоятельно. Как показывает опыт проведе­ния олимпиад различного уровня, решение таких задач требует от ученика определен­ной "интеллектуальной смелости" — приме­нить закон из одного раздела физики к дру­гому.

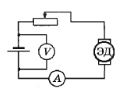
Пример 5. Электродвигатель включён в цепь, показанную на рисунке. На вал элек­тродвигателя намотана нить, к которой при­крепляют грузы различной массы, которые поднимаются при работе двигателя.

Оказалось, что при изменении сопротив­ления реостата не изменялись показания ни амперметра, ни вольтметра! Изменялась только скорость подъема груза. При измене­нии массы подвешенного груза сила тока в
цепи изменялась, причём оказалось, что сила тока в цепи работающего двигателя прямо пропорциональна массе поднимающе­гося груза I=km, где к — известный посто­янный коэффициент. Также известны: по­стоянное напряжение источника U_о; сопро­тивление обмотки электродвигателя R_o; пре­делы изменения сопротивления реостата: от нуля до R_m. Найдите зависимость скорости подъёма грузя от сопротивления реостата.

Для решения данной задачи требуется набраться мужества и записать уравнение за­кона сохранения энергии: мощность, разви­ваемая источником, равна сумме мощности теплоты, выделяющейся в цепи (закон Джо­уля—Ленца), и механической мощности, развиваемой при подъеме груза (хорошо зна­комое из механики выражение

Добавляя к этому уравнению формулу, приведённую в условии I=km, получаем систему двух уравнений с двумя неизвестными (сила тока и скорость подъё­ма). Решение этой системы и даёт искомый результат:

Далее можно предложить (неявно) про­анализировать полученный ответ: какова максимальная масса груза, которую способен поднять данный электродвигатель? Чему ра­вен КПД устройства?

1.7. Задачи должны быть решаемы!

Повторимся: школьный этап — первый в длинной цепочке олимлиаднмх испытаний, к участию в нём допускаются все желаю­щие, поэтому важно не вспугнуть начинаю­щих олимпийцев слишком сложными зада­чами  (невелика заслуга составить задачу, ко­торую никто не решит!). Не является боль­шим грехом включить в комплект вопросы, на которые ответит большинство участников.

Но но следует "обижать" участников олим­пиады, даже над такой задачей они должны слегка подумать.

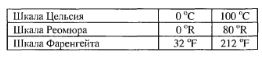
Пример 6*. Какую механическую рабо­ту необходимо совершить, чтобы нагреть полфунта воды, находящейся при температу­ре 122 ^oF (градуса Фаренгейта) до темпера­туры 72 ^oR  (градуса Реомюра)? Удельная теплоемкость воды равна

Один фунт равен 400 г.

Помимо знания формулы для количества теплоты, следует привести все исходные данные к одной системе единиц, к тому же вспомнить, чему равны калория и ускорение свободного падения.

{mospagebreak} 

2. Где взять идею олимпиадной задачи?

Не секрет, что многие задачи появляют­ся из сборников задач, причём многие из них постоянно диффундируют из одногосборника в другой (Не является исключением   и  данная статья,  так как приведенные здесь примеры взяты из сборников белорусских физически олимпиад). Тем не менее попыта­емся дать некоторые советы тем, кому легче придумать собственную задачу, чем найти нравящуюся в многочисленных учебно-мето­дических пособиях.

2.1. Учебники физики.

Любой физический закон требует не только зазубривания его формулировки и пе­ренесения формулы в шпаргалку, но, глав­ное, его понимания и осмысления. В каче­стве примера рассмотрим один из "простых"  законов — закон Архимеда. Физическая причина возникновения выталкивающей силы — давление жидкости на тело. Иными словами, выталкивающая сила есть вектор­ная сумма сил давления жидкости на отдель­ные малые участки поверхности тела.

Пример 7. Металлическая плита в фор­ме цилиндра радиусом Я, толщиной h и мас­сой m лежит на дне бассейна глубиной H (H>>h). Какую минимальную силу следует приложить к плите, чтобы поднять ее на поверхность? Какую минимальную работу сле­дует совершить для этого?

Нужно понимать, что когда плита лежит на дне, то давление жидкости на неё снизу не действует, поэтому силы Архимеда в обычном понимании нет. Чтобы оторвать плиту, следует преодолеть не только силу тя­жести плиты, но и силу давлении жидкости. Поэтому суммарная сила, направленная вниз

(р — плотность воды). Самое сложное — ото­рвать плиту от дна: если приложить ату к краю плиты, то ее минимальное значение должно быть в два раза меньше — вспомните правило рычага! После того как плита чуть-чуть оторвалась от дна, вода затекла под неё, т.е. начинает действовать сила Архиме­да, поэтому работа по подъёму

Аналогичная идея просматривается в том случае, когда какое-либо тело касается стен­ки сосуда — сила давления воды прижима­ет тело к стенке.

Также следует понимать, что закон Ар­химеда фактически выражает условие равно­весия тела и жидкости. Поэтому если тело находится в сосуде с жидкостью, который движется ускоренно, то сила Архимеда бу­дет направлена не вертикально!

Пример 8. Небольшой шарик объё­мом V падает на дно высокого бака, запол­ненного жидкостью плотностью р. Найдите силу давления жидкости на шарик, если бак движется горизонтально с постоянным уско­рением а.

При решении этой задачи необходи­мо учесть, что в данном случае сила Архи­меда

модуль этой силы

Из условия равновесия следует и точка приложения силы Архимеда — центр масс вытесненной жидкости.

Пример 9. Пробирка длимой l и радиу­сом r (r»l) плавает в воде. Каков должен быть уровень воды в пробирке, чтобы она могла устойчиво плавать вертикально от­крытым концом вверх? Масса пустой пробир­ки m.

В данном случае необходимо выполнение двух условий: во-первых, сила Архимеда должна уравновешивать силу тяжести (что является достаточно традиционным), во-вто­рых, центр масс пробирки с водой внутри должен находиться ниже центра масс вытес­ненной жидкости (который находится на по­ловине глубины погружения). Эти условия позволяют записать два неравенства, реше­ние которых и даст ответ задачи.

Чтобы возникла силы Архимеда, необхо­димо, чтобы давление в жидкости изменя­лось от точки к точке. Так, в невесомости давление в жидкости может присутствовать (например, пластиковая бутылка заполнена водой и сжата), причем во всех точках жид­кости одинаково, но сила Архимеда отсут­ствует. Задачу, основанную на этой идее. сформулируйте самостоятельно (в качестве домашнего задания).

Можно и далее приводить примеры задач на использование рассматриваемого закона. По мы ограничимся последним примером, в котором использование закона Архимеда так и напрашивается, но при внимательном ана­лизе задачи оказывается излишним.

Пример 10. В вертикальный цилиндри­ческий сосуд, частично заполненный водой, опускают деревянный кубик, объём которо­го равен V = 5.0 см³. Площадь поперечного сечения сосуда S = 6,0 см². На сколько поднимется уровень воды в сосуде после опускания кубика? Плотность дерева ρ=600 кг/м³, плотность воды ρ_о=1000 кг/м³.

Очередной раз вспоминаем об условиях равновесии и... при­меняем их ко всей жидкости вместе к кубиком. При опуска­нии кубика сила давления на дно сосуда возросла на величину силы тяже­сти кубика, поэтому

После записи этого соотношения можно смело готовиться к получению наград!

2.2. Лабораторные работы и демонстра­ционным эксперимент.

К сожалению, время от времени учите­лям физики приходится объяснять, почему результаты эксперимента не совпали с ре­зультатами теоретических расчетов. Одна из причин возможного несоответствия — неидеальность используемых измерительных при­боров (приходилось ли вам использовать в школе амперметр с нулевым сопротивлени­ем или вольтметр, сопротивление которого бесконечно велико?). Чем не источник для олимпиадных задач?

Прежде всего важно понимать, что ампер­метр показывает силу тока, проходящего че­рез него, вольтметр — напряжение на нём самом: приборы не могут "знать', что проис­ходит на других участках цепи.

Пример 11. В электрической цепи, со­стоящей из последовательно соединённых резистора, амперметра и вольтметра, сопро­тивление резистора равно 1,0 кОм, Показа­ние вольтметра 200 В, показание ампермет­ра 0,10 А. Чему равно сопротивление вольт­метра?

Понятно, что оно равно отношению на­пряжения (которое показывает вольтметр) к силе тока (которую показывает амперметр):

А заданное сопротивление резистора ни при чем!

Какой прибор — идеальный или нет, в некоторых случаях обязан определить сам учащийся!

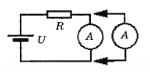
Пример 12. В цепи, показанной на ри­сунке, напряжение источника равно 4,0 В, сопротивление резистора 1,0 Ом, показания амперметра I. К амперметру параллельно подключают ещё один такой же амперметр. Чему равно показание этого амперметра?

Казалось бы? какая разница — получил формулу и подставил численные значения! Но следует сначала проанализировать усло­вие, подумать, что эти варианты принципи­ально различны. Действительно, проверим выполнение закона Ома. В первом случае полное соответствие:

что и поrазывает амперметр. Следовательно, ампер­метры иожно считать идеальными, поэтому при включении второго такого же ампермет­ра ток между ними разделится поровну, и амперметры будут показывать по 0,5 А. Во втором случае сила тока меньше, чем следу­ет из закона Ома, — единственной причиной этого является собственное сопротивление амперметра. Несложно определить, что оно 1,0 Ом. При включении
второго резистора сопротивление цепи станет равным 1,5 Ом, сила тока

а каждый из амперметров покажет половину этого значения.

Присмотритесь внимательно к проводи­мым экспериментам — всегда ли можно пренебречь трением, потерями теплоты, утечкой электрического заряда и т.д.

2.3. Справочники физических величин.

У многих учеников часто складывается твердое убеждение, что численные значения физических характеристик веществ есть нечто данное свыше (от бога или министерства). Между тем можно предложить ученикам по­искать закономерности в этих столбцах чисел. попробовать найти связи между различными характеристиками, особенно в тех случаях, когда эта связь может быть осмыслена.

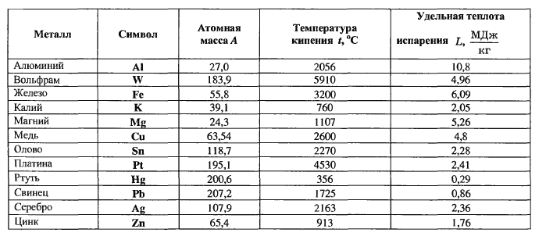
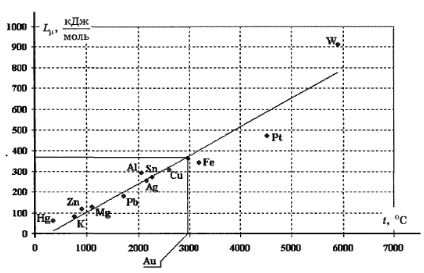
Пример 13. В таблице приведены зна­чения атомных масс А, температуры кипе­ния t_кип и удельной теплоты испарения L (при температуре кипения) для ряда металлов.

Используя данные таблицы, попытайтесь установить  функциональную связь (хотя бы приближенную) между приведёнными ха­рактеристиками металлов.

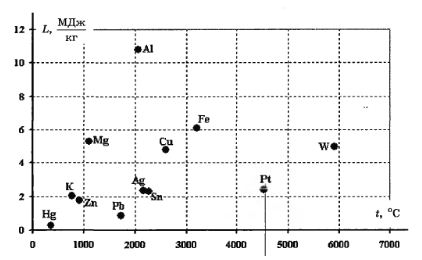
Можно, конечно, постараться найти эту связь методом случайного поиска, но такой путь очень сложен. Простое понимание физи­ческого смысла удельной теплоты испарения делает эту связь почти очевидной: чтобы жид­кость испарялась, ей необходимо сообщать теплоту — эта энергия затрачивается на пре­одоление сил межмолекулярного притяжения молекул в жидком состоянии. Чем сильнее связь между молекулами, тем большую энер­гию необходимо сообщить молекуле. Отдельная молекула преодолевает притяжение дру­гих молекул благодаря своей кинетической энергии (которая пропорциональна темпера­туре). Поэтому чем сильнее связь между мо­лекулами, тем выше должна быть теплота ис­парения и температура кипения. Следова­тельно, с ростом температуры должна возрас­тать и теплота испарения. Если нанести на диаграмму значения температуры кипения и удельной теплоты испарения, то никакой за­висимости не просматривается.

Однако если рассматривать теплоту испа­рения, приходящуюся на одну молекулу (или, что равносильно, на 1 моль — молярная теплота испарения  L_μ=LM), то наблю­дается практически линейная зависимость.

Можно найти много иных интересных связей: между удельной теплоёмкостью ме­таллов и их атомным весом, удельным элек­трическим сопротивлением и теплопроводно­стью (можно объяснить, что это такое, по аналогии); модулем Юнга, пределом прочно­сти и... коэффициентом теплового расшире­ния. Помимо того, что эти связи интересны, их поиск заставляет заглянуть внутрь строе­ния вещества.

2.4. Физические исторические экспери­менты.

В курсе физики средней школы рассмат­ривается множество физических экспери­ментов, сыгравших определенную роль в развитии физики. Начистую эти экспери­менты (в том числе и фундаментальные) описываются поверхностно. Предложите сво­им ученикам более тщательно разобраться в них. Приведём несколько примеров на эту тему.

Известно, что первая разумная оцен­ка скорости света была проведена О. Ремером на основании наблюдений за затмения­ми спутников Юпитера. Очень интересная кинематическая задача - рассчитать вре­мена этих затмений. Задайте закон измене­ния расстояния между Землей и Юпитером (чтобы не загромождать задачу геометричес­кими построениями), период обращения спутника, скорость света и порекомендуйте ученикам убедиться, что для получения ре­зультата Ремеру потребовался не один год наблюдений!

Предложите участникам олимиалды в не­которой упрощенной форме описать опыты штутгартского учителя физики Г. С. Ома. Как он сумел установить свой закон, не имея в своем кабинете ни амперметра, ни  вольтметра (даже школьных), ни электри­ческой розетки?

Не нужно брать эксперименты, заслу­жившие Нобелевские премии (оставьте их на заключительный этап олимпиады), пусть ученики тщательно опишут опыты Галилея по скатыванию шаров по наклонной плос­кости!

2.5. Любые другие источники.

Мы уже упоминали о таких мотивах за­дач, как природные явления, технические приложения, бытовые приборы. Нужно толь­ко внимательно наблюдать и обдумывать уви­денное. Можно также обращать внимание на
научно-популярные издания, статьи в газетах и журналах. Наконец, относительно недавно у нас появился еще один богатейший источ­ник — навязчивая реклама. Придумайте за­дачу, в которой необходимо оценить, на сколько процентов улучшается цвет лица (ко­торое можно заменить на лист белой бумаги). Или пример попроще. Некто рекламирует устройство, которое дает экономию "один киловатт в час" (!?). Если вам не удаётся скон­струировать такое устройство, то хотя бы при­думайте физическую величину, имеющую размерностью мощность, делённую на время!

Иными словами, окружающий нас мир на­столько богат, что трудно не найти тему для ин­тересной физической задачи. Обратите внимание, что в данной статье примеры подобраны по темам первых лет изучения физики — и они демонстрируют богатейшие возможности выбо­ра. А если обратиться к старшим классам?..