Волынец Е.Е. Еще раз об «оптимальном угле»
Волынец Ε.Ε. Еще раз об «оптимальном угле» // ФПВ. – 2004. – № 1. – С. 47-50.
С огромным интересом проработал статью В.Л. Акуленко «Оптимальный угол», которая напечатана в пятом номере за 2003 г. Автор совершенно верно поднимает вопрос об изменении скорости тела при изменении направления движения. К сожалению, авторы многих сборников не оговаривают механизм перехода тела с наклонной плоскости на горизонтальную поверхность и т.д. В задаче следует конкретнее определять вид взаимодействия тела с поверхностью (плавный переход или удар), определять тип удара (упругий или неупругий), также конкретизировать вид движения (равномерное или равноускоренное, прямолинейное или криволинейное). В зависимости от вида движения и вида удара будет по-разному изменяться импульс тела. Изменение импульса приведет к изменению характера дальнейшего движения. К сожалению, автор статьи лишь частично исследует изменение скорости движения тела при ударе. В задачах, приведенных В.Л. Акуленко, не рассматривается влияние силы трения в момент удара (например, в задачах с наклонной плоскостью). При переходе тела на горизонтальную поверхность будет наблюдаться удар. В качестве примера рассмотрим неупругий удар, продолжающийся некоторое конечное время. За это время сила трения успевает уменьшить и горизонтальную составляющую скорость. В момент удара наиболее существенно влияние сил, изменяющих скорость движения. Таковыми являются сила трения и сила реакции опоры.
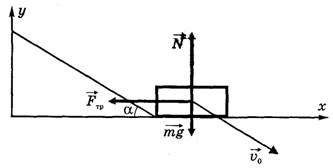
Согласно 2-му закону Ньютона:
![]()
Найдя проекции этого уравнения на оси координат и пренебрегая силой тяжести в момент удара, получим:
![]()
Разделив эти уравнения друг на друга, получим:
![]()
Из этого уравнения получим:
![]()
В данной задаче скорость будет меньше, чем ![]() (см.: «Фiзiка: праблемы выкладання», № 5, 2003 г.). Следовательно, будет меньше и расстояние, пройденное телом по горизонтальной поверхности, причем, если
(см.: «Фiзiка: праблемы выкладання», № 5, 2003 г.). Следовательно, будет меньше и расстояние, пройденное телом по горизонтальной поверхности, причем, если ![]() , тело остановится у основания наклонной плоскости.
, тело остановится у основания наклонной плоскости.
С учетом этого явления решение задач, представленных В.Л. Акуленко, выглядит несколько иначе.
№ 1. Под каким углом к горизонту следует расположить наклонную плоскость длиной l, чтобы тело, соскользнув с ее вершины, преодолело максимально возможный путь по горизонтальной поверхности? Трение на наклонном участке отсутствует, коэффициент трения на горизонтальном участке равен μ. Вертикальный удар считать неупругим.
Скорость тела у основания наклонной плоскости можно найти по закону сохранения энергии:
![]() ,
,
т.е. ![]() в свою очередь
в свою очередь ![]() , тогда
, тогда ![]()
Начальная скорость движения по горизонтали определяется способом, приведенным мной ранее:
![]() ,
,
или
![]()
По теореме об изменении кинетической энергии получим:
![]()
или
![]()
Торможение происходит на горизонтальном участке, поэтому
![]()
Тогда
![]()
Подставив значение скорости, можно найти путь, пройденный телом по горизонтали:
![]()
Для определения угла исследуем функцию на экстремум. Приравняв к нулю производную последней функции, найдем значение угла a, при котором скорость после удара, а, следовательно, и дальность будет максимальной:
![]()
Решение задач 2 и 3 предлагаю изменить самостоятельно.
Аналогично необходимо поступать при рассмотрении абсолютно упругого удара. В качестве примера приведу следующую задачу.
Мяч ударяется о плоскую поверхность под углом α к нормали, восстановленной в точке падения. Под каким углом β мяч отскочит от поверхности? Коэффициент трения мяча о поверхность равен μ.
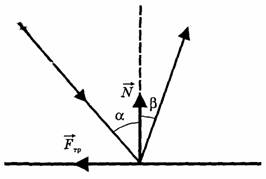
В данном случае удар вдоль оси у будем считать абсолютно упругим. За время удара будет потеряна скорость вдоль оси х. Пренебрегая действием силы тяжести, запишем изменение импульса вдоль каждой из осей:
![]()
Разделив эти уравнения друг на друга, получим:
![]()
Из этого уравнения можно найти х-ю составляющую скорости мяча после удара:
![]() .
.
При упругом ударе вертикальная составляющая скорости не изменится:
![]()
Тогда
![]() или
или ![]() .
.
Это решение имеет смысл, если ![]() . Если же это условие не выполняется, то β = 0.
. Если же это условие не выполняется, то β = 0.
Как видно из приведенных примеров, сила трения оказывает существенное влияние на дальнейшее движение тела. На мой взгляд, нельзя сравнивать взаимодействие конькобежца с ледяной горкой и взаимодействие тел с шероховатой поверхностью, как это делает автор статьи «Оптимальный угол».
В заключение хотелось бы предложить еще одну задачу, в которой рассматривается взаимодействие тела с шероховатой поверхностью.
Тело брошено с горизонтальной поверхности под углом α, равным 30° к горизонту, со скоростью u0 = 10 м/с. Считая вертикальный удар о поверхность упругим, определите расстояние между первым и вторым ударами. Коэффициент трения тела о поверхность μ = 0,366. Сопротивлением воздуха пренебречь.
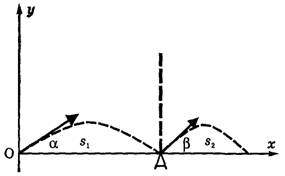
Если не учитывать сопротивление воздуха, то угол падения в точке А будет таким же, как и угол броска (30° к горизонту). Используя решение предыдущей задачи, можно найти угол β, под которым отскочит тело после первого удара:
![]()
![]()
Скорость вдоль оси x окажется равной (см. решение предыдущей задачи):
![]()
![]()
Вертикальная составляющая скорости в этом случае также не изменилась:
![]()
Скорость после первого удара окажется равной:
![]()
Дальность полета тела может быть найдена из кинематических законов движения тела, брошенного под углом к горизонту:
![]()
Интересным окажется сравнение этой дальности с дальностью полета без учета потери скорости при ударе. Если потери не учитывать, то:
s1 = s2 = s3 = s4 = ... = s,
s1 можно найти аналогично:
![]()
Как видно из полученного результата, расчеты отличаются более чем на 40%.
На мой взгляд, при формулировке задач необходимо конкретнее оговаривать явления, происходящие с телом в процессе движения. Разночтения возникают тогда, когда такой конкретности в условии нет.
| Выложил | alsak |
| Опубликовано | 20.07.07 |
| Просмотров | 9719 |
| Рубрика | Решение задач |
| Тема | Динамика Законы сохранения |