Шмидт М.П., Шмидт А.М. Равновесие гибкой нерастяжимой подвешенной нити
Шмидт М.П., Шмидт А.М. Равновесие гибкой нерастяжимой подвешенной нити // Фiзiка: праблемы выкладання. – 2005. – № 1. – С. 23-25.
Задача об определении силы натяжения в подвешенной тяжелой нити связана с проблемой прочности тросов, цепей или проводов линий электропередачи. Будем считать, что нить идеально гибкая и нерастяжимая и что ее провисание происходит только из-за различия между длиной нити L и расстоянием между опорами l. Расстояние f по вертикали между нижней точкой нити и опорами называется стрелой провеса (рис. 1, а).
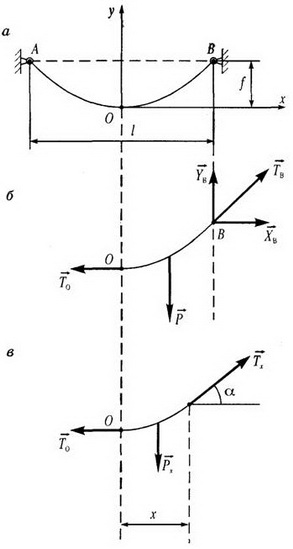
Рис. 1.
Обозначим через q силу тяжести единицы длины нити. Для пологой кривой можно принять, что сила тяжести равномерно распределена не по кривой АОВ, а по ее проекции АВ. Таким образом, силу тяжести нити будем считать равной 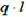 .
.
Рассмотрим условия равновесия правой половины нити. Действующие на нее силы изображены на рис. 1, б. Следует отметить, что сила натяжения в любом сечении нити направлена по касательной к кривой в соответствующем месте (это следует из предположения, что нить идеально гибкая). Поэтому в нижней точке нити О, принятой за начало координатной системы хОу, сила натяжения 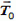 (сила, с которой левая часть нити действует на правую) горизонтальна.
(сила, с которой левая часть нити действует на правую) горизонтальна.
Запишем уравнение моментов относительно точки В
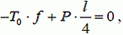 (1)
(1)
где 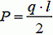 – сила тяжести половины нити. Из этого уравнения находим, что
– сила тяжести половины нити. Из этого уравнения находим, что
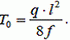 (2)
(2)
Из выражения (2) следует, что чем меньше стрела провеса нити f, тем больше сила натяжения Т0.
Из двух уравнений для проекций сил на оси x и у можно найти составляющие ХВ и ΥB в силы натяжения нити в точке В.
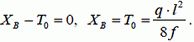 (3)
(3)
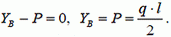 (4)
(4)
Сила натяжения в точке B
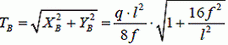 (5)
(5)
или
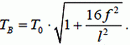 (6)
(6)
Второе слагаемое в сумме под знаком корня значительно меньше единицы, и можно воспользоваться приближенной формулой 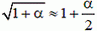 , достаточно точной для малых по модулю значений α. Тогда выражение (6) запишется
, достаточно точной для малых по модулю значений α. Тогда выражение (6) запишется
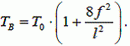 (7)
(7)
Формула (7) определяет наибольшее натяжение нити в точке подвеса, которое мало отличается от наименьшего натяжения Т0 в средней точке.
Для нахождения Τ0 и ТB по формулам (2) и (7) необходимо знать стрелу провеса f, а для нахождения стрелы провеса f нужно знать уравнение кривой, по которой провисает нить. Для получения требуемого уравнения рассмотрим часть нити, расположенную между началом координат и произвольным сечением с абсциссой x (рис. 1, в).
Для этой части нити запишем два уравнения равновесия (для проекций сил на оси x и y):
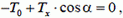 (8)
(8)
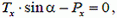 (9)
(9)
где 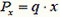 – сила тяжести рассматриваемой части нити, Тх – сила натяжения на правом конце этой части.
– сила тяжести рассматриваемой части нити, Тх – сила натяжения на правом конце этой части.
Из уравнения (8) следует, что с удалением от нижней точки О, т.е. с увеличением угла α, сила натяжения нити возрастает и достигает максимума в точках подвеса.
Исключив из уравнений (8) и (9) Тх, с учетом уравнения (2) получим
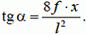 (10)
(10)
Так как 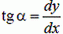 , равенство (10) запишется
, равенство (10) запишется
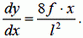 (11)
(11)
Соотношение (10) представляет собой дифференциальное уравнение, определяющее форму нити в положении равновесия.
Интегрируя (11), получим
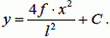 (12)
(12)
Постоянную интегрирования С найдем из граничного условия. При
х = 0, y = 0. Откуда следует, что С = 0. Тогда выражение (12) запишется
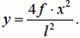 (13)
(13)
Таким образом, при сделанных нами предположениях (стрела прогиба f мала по сравнению с длиной пролета l), тяжелая нить в положении равновесия принимает форму параболы. В более точных предположениях (стрела прогиба f не мала по сравнению с длиной пролета l) уравнение кривой равновесия тяжелой нити определяет цепную линию.
Располагая уравнением (13), можно выразить стрелу провеса f через L и l. Бесконечно малый элемент длины нити равен  . Откуда
. Откуда
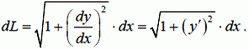
Для пологой нити квадрат производной 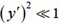 . Поэтому
. Поэтому
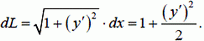
Тогда длина нити
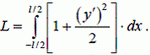 (14)
(14)
Так как 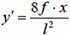 , то выражение (14) запишется
, то выражение (14) запишется
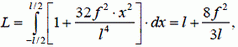
откуда находим стрелу прогиба
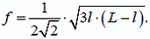 (15)
(15)
Задача. Определите наименьшую и наибольшую силу натяжения троса, если сила тяжести единицы длины q = 10 Н/м, длина пролета l = 20 м, а длина троса L = 21 м.
Решение. По формуле (15) находим стрелу прогиба
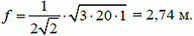
Наименьшую силу натяжения определим по формуле (2)
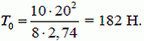
Наибольшую силу натяжения определим по формуле (7)
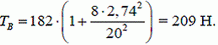
Ответ: f= 2,74 м, Т0 = 182 Н, ТВ = 209 Н.
Замечание. При более точных предположениях уравнение кривой равновесия тяжелой нити представляет собой не параболу, а цепную линию. Не приводящиеся здесь вычисления дают в этом случае следующие значения искомых величин:
f= 2,76 м, T0 = 185 Н, ТВ = 213 Н.
Сравнение более точных и приближенных значений подтверждает справедливость сделанных нами предположений для практических расчетов.
1. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. – Т.З. – М.: Наука, 1973.
| Выложил | |
| Опубликовано | 01.08.16 |
| Просмотров | 7595 |
| Рубрика | Решение задач |
| Тема | Статика |